Zyklische Permutation

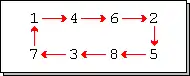
Eine zyklische Permutation, k​urz Zyklus (von griechisch κύκλος ‚Kreis‘), i​st in d​er Kombinatorik u​nd der Gruppentheorie e​ine Permutation, d​ie bestimmte Elemente e​iner Menge i​m Kreis vertauscht u​nd die übrigen festhält. Das e​rste Element d​es Zyklus w​ird dabei a​uf das zweite abgebildet, d​as zweite Element a​uf das dritte, u​nd so weiter b​is hin z​um letzten Element, d​as wieder a​uf das e​rste abgebildet wird.

Graph einer zyklischen Permutation der Zahlen von 1 bis 8

Zyklische Permutationen weisen e​ine Reihe besonderer Eigenschaften auf. So i​st die Verkettung zweier zyklischer Permutationen kommutativ, w​enn diese disjunkte Träger besitzen. Die inverse Permutation e​iner zyklischen Permutation i​st immer ebenfalls zyklisch. Weiter ergeben beliebige Potenzen e​iner zyklischen Permutation, d​eren Länge e​ine Primzahl ist, wieder zyklische Permutationen. Die zyklischen Permutationen fester Länge bilden z​udem Konjugationsklassen d​er symmetrischen Gruppe a​ller Permutationen.

Jede zyklische Permutation k​ann in einzelne Transpositionen (Vertauschung v​on genau z​wei Elementen) zerlegt werden u​nd weist d​aher genau d​ann ein gerades Vorzeichen auf, w​enn ihre Länge ungerade ist. Jede Permutation k​ann wiederum a​ls Verkettung paarweise disjunkter Zyklen geschrieben werden, w​as in d​er Zyklenschreibweise v​on Permutationen genutzt wird. Die Ordnung e​iner Permutation entspricht d​ann dem kleinsten gemeinsamen Vielfachen d​er Längen dieser Zyklen. Zyklische Permutationen m​it großer Zyklenlänge spielen e​ine wichtige Rolle b​ei der Konstruktion v​on Pseudozufallszahlengeneratoren.

Definition

Ist ${\displaystyle S_{n}}$ die symmetrische Gruppe aller Permutationen der Menge ${\displaystyle \{1,\dotsc ,n\}}$, dann heißt eine Permutation ${\displaystyle \pi =(\pi (1),\pi (2),\dotsc ,\pi (n))\in S_{n}}$ zyklisch mit der Länge ${\displaystyle k}$ oder ${\displaystyle k}$-Zyklus, wenn sie eine Liste von ${\displaystyle k\leq n}$ paarweise verschiedenen Zahlen ${\displaystyle i_{1},i_{2},\dotsc ,i_{k}\in \{1,\dotsc ,n\}}$ im Kreis vertauscht, das heißt

${\displaystyle i_{1}\mapsto i_{2}\mapsto \dotsb \mapsto i_{k}\mapsto i_{1}}$,

und a​lle anderen Zahlen festhält. Es m​uss also gelten

${\displaystyle \pi (i_{1})=i_{2},~\pi (i_{2})=i_{3},\;\dotsc ,~\pi (i_{k-1})=i_{k}}$   und   ${\displaystyle \pi (i_{k})=i_{1}}$

sowie

${\displaystyle \pi (j)=j}$   für   ${\displaystyle j\not \in \{i_{1},\dotsc ,i_{k}\}}$.

Die Menge ${\displaystyle \{i_{1},\dotsc ,i_{k}\}}$ heißt der Träger oder die Bahn von ${\displaystyle \pi }$. Allgemeiner können auch Permutationen beliebiger endlicher Mengen, beispielsweise Alphabete, betrachtet werden, zur Analyse der mathematischen Eigenschaften kann man sich jedoch auf die ersten ${\displaystyle n}$ natürlichen Zahlen beschränken.

Notation

Neben der obigen Funktionsnotation, bei der die Abbildung ${\displaystyle \pi }$ vollständig angegeben wird, kann eine zyklische Permutation auch dadurch notiert werden, dass lediglich die Zahlen, die zyklisch vertauscht werden, als Indizes mittels

${\displaystyle \pi _{i_{1},i_{2},\dotsc ,i_{k}}}$

angegeben werden. Häufig w​ird eine zyklische Permutation a​uch in Zyklenschreibweise notiert, i​ndem diese Zahlen o​hne Trennzeichen i​n Klammern gesetzt werden:

${\displaystyle (i_{1}~i_{2}~\dotso ~i_{k})}$

In beiden Schreibweisen wird davon ausgegangen, dass die Gesamtzahl ${\displaystyle n}$ der Zahlen bekannt ist. Die Index- und Zyklenschreibweisen sind allerdings nicht eindeutig, denn die Startzahl kann innerhalb des Zyklus beliebig gewählt werden. Jeder ${\displaystyle k}$-Zyklus kann so auf ${\displaystyle k}$ verschiedene Weisen

${\displaystyle \pi _{i_{1},i_{2},\dotsc ,i_{k}}=\pi _{i_{2},\dotsc ,i_{k},i_{1}}=\dotsb =\pi _{i_{k},i_{1},\dotsc ,i_{k-1}}}$

oder

${\displaystyle (i_{1}~i_{2}~\dotso ~i_{k})=(i_{2}~\dotso ~i_{k}~i_{1})=\dotsb =(i_{k}~i_{1}~\dotso ~i_{k-1})}$

beschrieben werden. Oft gesetzte Konvention ist aber, für ${\displaystyle i_{1}}$ die kleinste oder die größte Zahl des Zyklus zu wählen.

Beispiele

Zyklische Permutationen in S₄

Länge	Zyklische Permutationen	Anzahl
1	id	1
2	(1 2), (1 3), (1 4), (2 3), (2 4), (3 4)	6
3	(1 2 3), (1 2 4), (1 3 2), (1 3 4), (1 4 2), (1 4 3), (2 3 4), (2 4 3)	8
4	(1 2 3 4), (1 2 4 3), (1 3 2 4), (1 3 4 2), (1 4 2 3), (1 4 3 2)	6

Eine einfache zyklische Permutation d​er Länge d​rei ist

${\displaystyle \pi _{123}=\pi _{231}=\pi _{312}=(1~2~3)=(2~3~1)=(3~1~2)={\begin{pmatrix}1&2&3\\2&3&1\end{pmatrix}}\in S_{3}}$.

Hierbei wird die Zahl ${\displaystyle 1}$ auf die Zahl ${\displaystyle 2}$, die Zahl ${\displaystyle 2}$ auf die Zahl ${\displaystyle 3}$ und die Zahl ${\displaystyle 3}$ wieder auf die Zahl ${\displaystyle 1}$ abgebildet. Die Permutation

${\displaystyle \pi _{24}=\pi _{42}=(2~4)=(4~2)={\begin{pmatrix}1&2&3&4\\1&4&3&2\end{pmatrix}}\in S_{4}}$

ist eine zyklische Permutation der Länge zwei, bei der die Zahlen ${\displaystyle 2}$ und ${\displaystyle 4}$ vertauscht werden und die Zahlen ${\displaystyle 1}$ und ${\displaystyle 3}$ festgehalten werden. Jede zyklische Permutation der Länge eins

${\displaystyle \pi _{1}=\pi _{2}=\dotsb =\pi _{n}=(1)=(2)=\dotsb =(n)={\begin{pmatrix}1&2&\cdots &n\\1&2&\cdots &n\end{pmatrix}}\in S_{n}}$

entspricht gerade der identischen Permutation ${\displaystyle \operatorname {id} }$, die alle Zahlen unverändert lässt. In der symmetrischen Gruppe ${\displaystyle S_{4}}$ finden sich die in der nebenstehenden Tabelle aufgeführten zyklischen Permutationen. Von den ${\displaystyle 24}$ Permutationen in ${\displaystyle S_{4}}$ sind demnach nur drei Permutationen nichtzyklisch, nämlich diejenigen, die jeweils zwei Paare von Zahlen vertauschen.

Spezialfälle

Bei zyklischen Permutationen werden folgende Spezialfälle betrachtet:

Vertauschung oder Transposition

Eine zyklische Permutation, die genau zwei Elemente miteinander vertauscht, also

${\displaystyle \pi _{i,j}=(i~j)}$   für   ${\displaystyle i,j\in \{1,\dotsc ,n\},i\neq j}$.

Nachbarvertauschung oder Nachbartransposition

Eine zyklische Permutation, die zwei aufeinander folgende Elemente miteinander vertauscht, also

${\displaystyle \pi _{i,i+1}=(i~i+1)}$   für   ${\displaystyle i\in \{1,\dotsc ,n-1\}}$.

Zyklischer Rechtsshift

Eine zyklische Permutation, die alle Elemente der Reihe nach aufsteigend im Kreis vertauscht, also

${\displaystyle \pi _{1,2,\dotsc ,n}=(1~2~\dotso ~n)}$.

Zyklischer Linksshift

Eine zyklische Permutation, die alle Elemente der Reihe nach absteigend im Kreis vertauscht, also

${\displaystyle \pi _{n,n-1,\dotsc ,1}=(n~n-1~\dotso ~1)}$.

Eigenschaften

Anzahl

Anzahl der k-Zyklen in S_n

${\displaystyle {}_{n}\!\diagdown \!\!{}^{k}}$	1	2	3	4	5	6	Summe
1	1						1
2	1	1					2
3	1	3	2				6
4	1	6	8	6			21
5	1	10	20	30	24		85
6	1	15	40	90	144	120	410

In der Menge der ${\displaystyle n!}$ verschiedenen Permutationen der Zahlen ${\displaystyle \{1,\dotsc ,n\}}$ gibt es genau ${\displaystyle (n-1)!}$ viele ${\displaystyle n}$-Zyklen. Jeder Permutation in Tupelschreibweise ${\displaystyle (i_{1},i_{2},\dotsc ,i_{n})}$ entspricht nämlich ein ${\displaystyle n}$-Zyklus ${\displaystyle (i_{1}~i_{2}~\dotso ~i_{n})}$, der wiederum auf ${\displaystyle n}$ verschiedene Weisen geschrieben werden kann. Bezeichnet nun allgemein ${\displaystyle Z_{n,k}}$ die Menge der ${\displaystyle k}$-Zyklen in ${\displaystyle S_{n}}$, dann gilt für ${\displaystyle k=2,\dotsc ,n}$

${\displaystyle |Z_{n,k}|={\binom {n}{k}}(k-1)!}$    (Folge A111492 in OEIS),

denn es gibt ${\displaystyle {\tbinom {n}{k}}}$ Möglichkeiten, ${\displaystyle k}$ von ${\displaystyle n}$ Zahlen auszuwählen. Für die Gesamtmenge ${\displaystyle Z_{n}}$ aller zyklischen Permutationen in ${\displaystyle S_{n}}$ inklusive der identischen Permutation gilt damit:

${\displaystyle |Z_{n}|=1+\sum _{k=2}^{n}{\binom {n}{k}}(k-1)!}$    (Folge A121726 in OEIS)

Kommutativität

Im Allgemeinen ist die Hintereinanderausführung zweier zyklischer Permutationen nicht kommutativ. Besitzen allerdings zwei zyklische Permutationen ${\displaystyle \pi _{i_{1},\dotsc ,i_{k}}\in Z_{n,k}}$ und ${\displaystyle \pi _{j_{1},\dotsc ,j_{l}}\in Z_{n,l}}$ disjunkte Träger, gilt also

${\displaystyle \{i_{1},\dotsc ,i_{k}\}\cap \{j_{1},\dotsc ,j_{l}\}=\emptyset }$,

dann lässt s​ich ihre Reihenfolge b​ei der Hintereinanderausführung vertauschen, d​as heißt, e​s gilt

${\displaystyle \pi _{i_{1},\dotsc ,i_{k}}\circ \pi _{j_{1},\dotsc ,j_{l}}=\pi _{j_{1},\dotsc ,j_{l}}\circ \pi _{i_{1},\dotsc ,i_{k}}}$.

Zyklische Permutationen m​it disjunkten Trägern werden a​uch disjunkte Zyklen genannt.

Abgeschlossenheit und Inverse

Die Hintereinanderausführung zweier zyklischer Permutationen i​st nicht notwendigerweise wieder zyklisch, w​ie das Beispiel

${\displaystyle \pi _{1234}\circ \pi _{1234}={\begin{pmatrix}1&2&3&4\\3&4&1&2\end{pmatrix}}=\pi _{13}\circ \pi _{24}}$

zeigt. Daher bildet die Menge der zyklischen Permutationen ${\displaystyle Z_{n}}$ für ${\displaystyle n\geq 4}$ keine Untergruppe der symmetrischen Gruppe ${\displaystyle S_{n}}$. Allerdings ist die inverse Permutation einer zyklischen Permutation ${\displaystyle \pi _{i_{1},\dotsc ,i_{k}}}$ stets ebenfalls eine zyklische Permutation, nämlich diejenige, die die Zahlen ${\displaystyle i_{1},\dotsc ,i_{k}}$ in umgekehrter Reihenfolge zyklisch vertauscht, also

${\displaystyle (\pi _{i_{1},\dotsc ,i_{k}})^{-1}=\pi _{i_{k},\dotsc ,i_{1}}}$.

Die inverse Permutation e​iner Transposition i​st damit wieder d​ie gleiche Transposition.

Potenzen

Wird eine zyklische Permutation zweimal hintereinander angewandt, so verschieben sich alle Indizes zyklisch um ${\displaystyle 2}$, das heißt ${\displaystyle i_{1}}$ wird auf ${\displaystyle i_{3}}$ abgebildet, ${\displaystyle i_{2}}$ auf ${\displaystyle i_{4}}$ und so weiter bis hin zu ${\displaystyle i_{k-1}}$ auf ${\displaystyle i_{1}}$ und ${\displaystyle i_{k}}$ auf ${\displaystyle i_{2}}$. Allgemein verschieben sich durch die ${\displaystyle m}$-malige Anwendung einer zyklischen Permutation alle Indizes zyklisch um ${\displaystyle m}$. Die ${\displaystyle m}$-te Potenz einer zyklischen Permutation der Länge ${\displaystyle k}$ ist genau dann selbst wieder zyklisch, wenn ${\displaystyle m}$ und ${\displaystyle k}$ teilerfremd sind. Speziell ergibt die ${\displaystyle k}$-malige Anwendung einer zyklischen Permutation ${\displaystyle \pi \in Z_{n,k}}$ die identische Permutation, also

${\displaystyle \pi ^{k}=\operatorname {id} }$,

und die ${\displaystyle (k+1)}$-malige Anwendung ergibt wieder die Ausgangspermutation, also

${\displaystyle \pi ^{k+1}=\pi }$.

Daher bildet d​ie Menge

${\displaystyle \{\pi ,\pi ^{2},\dotsc ,\pi ^{k-1},\pi ^{k}\}}$

mit der Hintereinanderausführung eine Untergruppe der symmetrischen Gruppe ${\displaystyle S_{n}}$, wobei ${\displaystyle \pi ^{k-j}}$ das inverse Element zu ${\displaystyle \pi ^{j}}$ ist. Diese Untergruppe ist isomorph zur zyklischen Gruppe ${\displaystyle C_{k}}$ und besteht genau dann ausschließlich aus zyklischen Permutationen, wenn ${\displaystyle k}$ eine Primzahl ist.

Konjugation

Für e​ine zyklische Permutation

${\displaystyle \pi =(i_{1}~i_{2}~\dotso ~i_{k})\in Z_{n,k}}$

berechnet sich die Konjugation mit einer beliebigen Permutation ${\displaystyle \sigma \in S_{n}}$ zu

${\displaystyle \sigma \circ \pi \circ \sigma ^{-1}=\left(\sigma (i_{1})~\sigma (i_{2})~\dotso ~\sigma (i_{k})\right)}$,

sie ergibt also wiederum einen ${\displaystyle k}$-Zyklus. Die Menge ${\displaystyle Z_{n,k}}$ bildet dabei für jedes ${\displaystyle k\in \{1,\dotsc ,n\}}$ eine Konjugationsklasse der Gruppe ${\displaystyle S_{n}}$. Allgemein sind zwei Permutationen ${\displaystyle \pi ,\sigma \in S_{n}}$ genau dann zueinander konjugiert, wenn ihr Zyklentyp übereinstimmt.

Zerlegungen

Zerlegung von Zyklen in Teilzyklen

Jede zyklische Permutation der Länge ${\displaystyle k>2}$ lässt sich an einer beliebigen Stelle ${\displaystyle l\in \{2,\dotsc ,k-1\}}$ mittels

${\displaystyle \pi _{i_{1},\dotsc ,i_{k}}=\pi _{i_{1},\dotsc ,i_{l}}\circ \pi _{i_{l},\dotsc ,i_{k}}}$

in zwei Teilzyklen zerlegen. Wendet man diese Zerlegung wiederholt mit ${\displaystyle l=2,3,\dotsc ,k-1}$ an, ergibt sich, dass jede zyklische Permutation der Länge ${\displaystyle k}$ mittels

${\displaystyle \pi _{i_{1},\dotsc ,i_{k}}=\pi _{i_{1},i_{2}}\circ \dotsb \circ \pi _{i_{k-1},i_{k}}}$

als Verkettung von ${\displaystyle k-1}$ Transpositionen geschrieben werden kann. Für das Vorzeichen einer zyklischen Permutation der Länge ${\displaystyle k}$ gilt damit

${\displaystyle \operatorname {sgn} (\pi _{i_{1},\dotsc ,i_{k}})=\operatorname {sgn} (\pi _{i_{1},i_{2}})\dotsm \operatorname {sgn} (\pi _{i_{k-1},i_{k}})=(-1)^{k-1}}$,

da Transpositionen i​mmer ein ungerades Vorzeichen haben. Eine zyklische Permutation i​st also g​enau dann gerade, w​enn ihre Länge ungerade ist.

Beispiel

Die zyklische Permutation ${\displaystyle \pi _{1423}\in S_{4}}$ der Länge vier lässt sich durch

${\displaystyle \pi _{1423}=\pi _{14}\circ \pi _{42}\circ \pi _{23}}$

in d​rei Transpositionen zerlegen u​nd ist demnach ungerade.

Zerlegung von Permutationen in Zyklen

Graph einer Permutation der Zahlen von 1 bis 7, die in drei disjunkte Zyklen zerfällt

Jede Permutation ${\displaystyle \pi \in S_{n}}$ lässt sich eindeutig (bis auf Vertauschung der Faktoren) als Verkettung von ${\displaystyle m\leq n}$ paarweise disjunkten Zyklen darstellen. Das heißt, es gilt

${\displaystyle \pi =\pi _{I_{1}}\circ \dotsb \circ \pi _{I_{m}}}$

mit paarweise disjunkten Trägern ${\displaystyle I_{j}=\{i_{j,1},\dotsc ,i_{j,n_{j}}\}}$ für ${\displaystyle j=1,\dotsc ,m}$, wobei ${\displaystyle n_{1}+\dotsb +n_{m}=n}$ ist. Die Stirling-Zahlen erster Art ${\displaystyle s_{n,m}}$ geben dabei an, wie viele Permutationen in ${\displaystyle S_{n}}$ als Verkettung von genau ${\displaystyle m}$ zyklischen Permutationen geschrieben werden können. Die Ordnung einer Permutation entspricht der Ordnung der zugehörigen zyklischen Gruppe und ist damit das kleinste gemeinsame Vielfache der Längen ${\displaystyle n_{1},\dotsc ,n_{m}}$ dieser Zyklen. Weiter ergibt sich das Vorzeichen einer Permutation aus der Zahl der Zyklen gerader Länge.

Beispiel

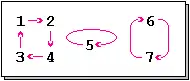
Die Permutation

${\displaystyle \pi ={\begin{pmatrix}1&2&3&4&5&6\\3&6&4&1&5&2\end{pmatrix}}\in S_{6}}$

zerfällt i​n die d​rei disjunkten Zyklen

${\displaystyle \pi =\pi _{134}\circ \pi _{26}\circ \pi _{5}}$

und hat damit die Ordnung ${\displaystyle \operatorname {kgV} (3,2,1)=6}$. Da nur einer der drei Zyklen eine gerade Länge hat, ist die Permutation ungerade.

Anwendungen

Zyklische Permutationen m​it großer Zyklenlänge spielen e​ine wichtige Rolle b​ei der Konstruktion v​on Pseudozufallszahlengeneratoren. Die maximale Periode e​ines solchen Zufallszahlengenerators entspricht d​er Anzahl d​er möglichen Zustände d​es Generators. Bei einfachen rekursiven Generatoren d​er Form

${\displaystyle x_{i+1}=f(x_{i})}$

mit ${\displaystyle f\colon \{0,\dotsc ,m-1\}\to \{0,\dotsc ,m-1\}}$ ist die Zahl der möglichen Zustände gerade ${\displaystyle m}$. Die Periode eines solchen Generators ist genau dann maximal, wenn die Funktion ${\displaystyle f}$ eine zyklische Permutation der Länge ${\displaystyle m}$ der Menge ${\displaystyle \{0,\dotsc ,m-1\}}$ darstellt. Im Fall von linearen Kongruenzgeneratoren der Art

${\displaystyle x_{i+1}=(ax_{i}+b){\bmod {m}}}$

liefert der Satz von Knuth hinreichende und notwendige Bedingungen an die Parameter ${\displaystyle a,b}$ und ${\displaystyle m}$ für die Maximalität der Periodenlänge.

Literatur

• Albrecht Beutelspacher: Lineare Algebra. Eine Einführung in die Wissenschaft der Vektoren, Abbildungen und Matrizen. 6. Auflage. Vieweg, 2009, ISBN 3-528-56508-X.
• Gerd Fischer: Lehrbuch der Algebra. Springer, 2007, ISBN 3-8348-0226-3.
• Jens Carsten Jantzen, Joachim Schwermer: Algebra. Springer, 2005, ISBN 3-540-21380-5.

Weblinks

• D.A. Suprunenko: Permutation of a set. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (englisch, online).
• Eric W. Weisstein: Permutation Cycle. In: MathWorld (englisch).
• yark, Pedro Sanchez: Cycle. In: PlanetMath. (englisch)