Tibetische Maßeinheiten
Tibetische Maßeinheiten dienten in Tibet der Bestimmung der Größen von Gegenständen des täglichen Lebens, von geometrischen Konstruktionszeichnungen der Malerei, von Unterteilungen der Ekliptik in der Astronomie und der Zeit nach den Größenarten Länge, Volumen, Gewicht und Zeitintervall. Bestimmte Gegenstände des täglichen Lebens, wie beispielsweise Getreidemengen, wurden in Tibet nicht gewogen, sondern mit einem Volumenmaß gemessen.
Längenmaße
Bei den Längenmaßen wurde zwischen Maßeinheiten, deren Größen anhand eines festen Messstabes festgelegt waren, die also eine festgelegte absolute Größe hatten, und Proportionalmaßen sowie Bogen- bzw. Winkelmaßen unterschieden.
Längenmaße des alltäglichen Lebens
Die kleinste, im tibetischen Wirtschaftsleben praktisch verwendete Längeneinheit war das sor-mo („Fingerbreite“), welche der angenommenen Breite eines Fingers entsprach. 12 sor-mo bilden ein mtho („Spanne“, in Tibet Spannweite zwischen Zeigefinger und Daumen). 2 mtho entsprechen einem khru (Elle) und 4 khru bilden ein rang 'dom bzw. ein 'dom (Klafter).
Zu diesem Maßsystem ist uns auch ein entsprechender Messstab überliefert, der die Länge von 182 cm besitzt.[1] Der Stab ist durch umlaufende Einkerbungen in 8 gleich große Teile geteilt. Das letzte dieser 8 Teile weist wiederum eine Unterteilung in 12 Teile auf, die von 1 bis 12 fortlaufend nummeriert sind. Hierbei handelt es sich um die Maßeinheit sor-mo.
Anhand der Länge des Messstabes ergibt sich für einen Klafter (tib.: 'dom) die Größe 182 cm. Die Elle (tib.: khru) misst somit 45,5 cm. Eine Spanne (tib.: mtho) entspricht 22,75 cm und eine Fingerbreite (tib.: sor-mo) ist aufgerundet 1,896 cm groß. Aufgrund der Beschaffenheit dieses Messstabes ist davon auszugehen, dass das Messinstrument nicht als Lineal zum Zeichnen von Linien verwendet wurde.
Es ist anzunehmen, dass die absolute Größe dieser Längeneinheiten in den unterschiedlichen Landesteilen Tibets verschieden war.
Längenmaße des Kālacakratantra
In dem Längenmaßsystem, welches durch das Kālacakrantra aus Indien nach Tibet überliefert wurde, wird die kleinste Einheit mit sehr feiner Staub angegeben (tib.: phra-rab rdul; Sanskrit: sūkṣma), welches die Größe von
einer Fingerbreite (tib.: sor-mo) hat. Dies entspricht circa 0,000072 Millimeter. Die größte Einheit wird mit dpag-tshad (Sanskrit: yojana) bezeichnet. Eine solche dpag-tshad umfasst 32.000 Ellen, also circa 14,56 km.
Praktische Verwendung fand dieses Maßsystem in Tibet nur bei der Beschreibung der Größe des Aufbaus der Welt, wobei hier nur die Maßeinheit dpag-tshad von Bedeutung war.
Tabelle der Maßeinheiten:
| Umrechnungsfaktor zur nächsthöheren Einheit | Bezeichnung (Tibetisch) | Bezeichnung (Sanskrit) | Bedeutung | Ungefähre Länge | |||||
|---|---|---|---|---|---|---|---|---|---|
| 8 | phra rab rdul | sūkṣma | sehr feiner Staub | 0,000072 Millimeter | |||||
| 8 | phra mo | aṇu | feiner (Staub) | 0,000576 Millimeter | |||||
| 8 | skra yi rtse mo | vālāgra | Haarspitze | 0,0046 Millimeter | |||||
| 8 | ske tshe | rāji | Senfkorn | 0,037 Millimeter | |||||
| 8 | shig | yūkā | Laus | 0,296 Millimeter | |||||
| 8 | nas | yava | Gerstenkorn | 2.368 Millimeter | |||||
| 24 | sor mo | aṅgula | Fingerbreite | 1,896 Zentimeter | |||||
| 4 | khru | hasta | Elle | 45,5 Zentimeter | |||||
| 2000 | gzhu | dhanus | Bogenlänge | 1,82 Meter | |||||
| 4 | rgyang grags | krośa | Rufweite | 3,640 Kilometer | |||||
| dpag tshad | yojana | 14,56 Kilometer |
Proportionalmaße der tibetischen Malerei
Auf Konstruktionszeichnungen tibetischer Thangkas, die wie ein Koordinatennetz gezeichnet werden, finden sich Zahlenangaben über die Abstände der einzelnen Linien, deren Grundgröße ebenfalls als sor „Fingerbreite“ bezeichnet wird. Hierbei handelt es sich aber nicht um ein festes Längenmaß, das eine fest fixierte Länge hat, wie etwa das Längenmaß „Meter“, sondern um ein sogenanntes Proportionalmaß. Dabei ist die Grundgröße, an der man sich bei einer bestimmten Zeichnung bzw. Konstruktion orientiert, die Breite des Mittelfingers der Darstellung der jeweiligen Person oder Gottheit in der Zeichnung. Diese Grundgröße wurde entsprechend auch sor „Fingerbreite“ genannt.
In Abhängigkeit von der Größe der Zeichnung besaßen diese Sor-Maßgrößen also absolut genommen unterschiedliche Längen. Allerdings war die Größe des sor innerhalb einer Zeichnung immer gleich. Die Proportionalmaßgrößen besaßen je nach ihrer relativen Größe unterschiedliche Bezeichnungen. Die kleinste Einheit wurde nas „Gerstenkorn“ genannt. 2 nas entsprachen einem rkang und 4 rkang ergaben ein sor, das auch cha-chung „kleines Teil“ genannt wurde. Die nächste größere Einheit war ein cha-chen „großes Teil“, das 12 sor umfasste.
Winkelmaße
.jpg.webp)

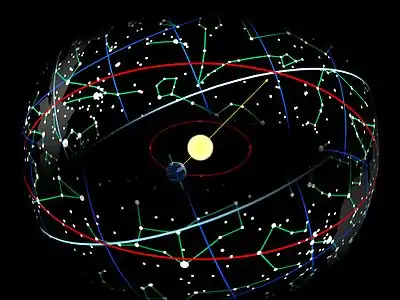
Winkelmaße kommen in der tibetischen Astronomie vor, die sich insbesondere mit der Berechnung der Positionen – astronomisch Längen genannt – des Mondes, der Sonne und der Planeten Merkur, Venus, Mars, Jupiter und Saturn beschäftigt. Hierbei ist im geozentrischen Weltbild der Tibeter die Sonne ein Planet.
Der Großkreis, der durch die Projektion der scheinbaren Bahn der Sonne im Verlauf eines Jahres auf der Himmelskugel entsteht, wird Ekliptik genannt. Auf ihm bewegen sich vom Standpunkt der Erde aus gesehen bei geringfügigen Abweichungen in der sogenannten Breite alle Planeten einschließlich des Mondes.
Die erste hier zu erwähnende Aufteilung dieses Großkreises in Tibet ist die in 12 Tierkreiszeichen, die tibetisch als khyim bezeichnet wurden. Wie auf der Abbildung rechts oben rot dargestellt ist, trugen diese Tierkreiszeichen zwar Namen, aber für die astronomischen Berechnungen wurden sie mit den Zahlen 0 bis 11 gezählt und bezeichnet. Das Gleiche gilt für die Einteilung der Ekliptik in die sogenannten 27 Mondhäuser bzw. Mondstationen, die tibetisch als rgyu-skar bezeichnet wurden und die, wie auf der Abbildung links unten in blauer Farbe dargestellt ist, von 0 bis 26 gezählt wurden.
Die Bogen- bzw. Winkelmaßeinheit rgyu skar wurde in 60 chu tshod „Bogenstunden“ unterteilt. Die chu tshod wurden in 60 chu srang „Bogenminuten“ unterteilt. Eine chu srang bestand aus 6 dbugs „Bogenatemzug“, die wiederum in „Teile“ unterteilt wurden. Es wird deutlich, dass mit diesem System von Winkelmaßen die Länge eines Planeten sehr genau bestimmt werden konnte.
Der rechts abgebildete Ausschnitt aus einem tibetischen astronomischen Thangka zeigt im 5. Kreis von außen die Mondhäuser 20 chu smad, 21 gro bzhin und 22 mon gre, im dritten Kreis sind die Tierkreiszeichen 8 gzhu und 9 chu srin eingezeichnet. Die Einteilung der Mondhäuser in chu tshod ist mit den Zahlen 15, 30, 45 und 60 dargestellt.
Tabelle der Winkelmaße:
| Voller Kreis: | 12 khyim | 360 Grad | 27 rgyu skar | 360 Grad | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1. Unterteilung: | 1 khyim | 30 Grad | 1 rgyu skar= 60 chu tshod | 13 Grad und 20 Bogenminuten | |||||
| 2. Unterteilung: | 1 chu tshod= 60 chu srang | 13 Bogenminuten und 20 Bogensekunden | |||||||
| 3. Unterteilung: | 1 chu srang= 6 dbugs | 13 + 1/3 Bogensekunden | |||||||
| 4. Unterteilung: | dbugs | 2 + 2/9 Bogensekunden |
Hohlmaße


Getreide, Hülsenfrüchte u. ä. wurden in Tibet nicht gewogen, sondern mit Messkasten gemessen. Diese wurden 'bo oder bogs 'bo genannt. Die damit gegeben größte Maßeinheit nannte man ein khal. Ein khal wurde in 20 bre unterteilt. Jedes bre umfasste 6 phul („handvoll“). Es gab unterschiedliche Messkasten zur Messung der khal und der bre.
Die Größe dieser Messkasten war je nach Landesteil sehr verschieden. Die zentraltibetische Regierung etablierte im 17. Jahrhundert mit einem entsprechend geeichten Messkasten ein für das Schatzamt verbindliches Normmaß für das khal. Das zugehörige Messgerät wurde mkhar ru oder gtan tshigs mkhar ru genannt. Das Gewicht des Getreides, welches mit einem solchen Messgerät gemessen wurde, dürfte circa 15 kg betragen haben. Die Angaben von Tibetreisenden zum Gewicht dieses Norm-khal sind sehr unterschiedlich. Dabei ist auch zu beachten, dass das Gewicht einer Getreidemenge, die mit einem Volumenmaß gemessen wird, je nach Größe der Getreidekörner und nach deren Wassergehalt sehr unterschiedlich ausfallen kann.
Wenn man eine ungefähre Dichte von 0,8 g/cm³ für Getreide annimmt, entspräche also ein khal ungefähr einem Volumen von 18750 cm³, also 18,75 Liter. Ein bre wäre also etwas weniger als 1 Liter.
Die Umrechnung der mit den verschiedenartigen Messkasten ermittelten Größen von Getreidemengen auf das Standardmaß der Regierung wurde von den Amtsträgern im tibetischen Schatzamt mit dem Abakus mit losen Steinen durchgeführt. Um dabei das Problem der Entstehung von Resten rechnerisch in den Griff zu bekommen, wurde die Maßgröße phul in 120 nang gi rdog ma „Innere Stücke“ unterteilt. Weitere Unterteilungen führten zu Größeneinheiten, deren Größe khal betrug.
Tabelle der Hohlmaße:
| Bezeichnung (Tibetisch): | khal | bre | phul | nang gi rdog ma | phyi ma´i rdog ma | de´i phyi ma´i rdog ma | yang phyi rdog ma | mthil phyi rdog ma | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Umrechnungsfaktor zur nächsthöheren Einheit: | 20 | 6 | 120 | 120 | 120 | 120 | 120 |
- |
Gewichtsmaße

Bei den Gewichtsmaßeinheiten unterschied man Maßeinheiten zum Wiegen von Edelmetallen und Maßeinheiten für das Gewicht von Butter, Fleisch, Holz usw.
Gewichtsmaßeinheiten für Gold
Die kleinste Einheit der Goldgewichte wurde nas „Gerstenkorn“ genannt. Zwei Gerstenkörner sind ein ma nu. Davon 2 sind ein se ba. Davon bilden 2 ein gser tam. 15 gser tam ergeben ein zho.[2] Die Größe dieser Goldgewichte variierte regional stark. Für eine Übersicht hierzu siehe Historische Währung Tibets.
Gewöhnliche Gewichtsmaße

Zum Wiegen von Butter, Fleisch, Holz, Heu usw. wurden in Tibet Balkenwaagen verwendet, die verschiebbare Gewichtssteine besaßen.
Die größte Gewichtseinheit wurde ebenfalls als khal bezeichnet. Dieses Gewichts-khal war gleich 20 nyag. Auf ein nyag kamen 4 spor.
Zeitgrößen
Zeiteinteilung nach dem tibetischen Kalender
Die in Tibet bekannten Zeitintervalle waren das Jahr (tib.: lo), Monat (tib.: zla ba), Tag (tib.: zhag) und Tageszeit (tib.: dus tshod). Für Details dieser komplizierten Zeitaufteilung siehe Tibetischer Kalender.
Astronomische Tageseinteilung
Die drei verschiedenen Tagesarten, die im tibetischen Kalender aufgeführt sind, nämlich der Zodiak-Tag, der Lunare Tag und der Natürliche Tag wurden für astronomische Berechnungen analog zur Aufteilung der Ekliptik in die Zeitintervalle chu tshod „Stunde“, chu srang „Minute“ und dbugs „Länge eines Atemzuges“ unterteilt. Dabei umfasste ein Tag 60 chu tshod. Eine chu tshod wurde in 60 chu srang unterteilt. Eine chu srang bestand aus 6 dbugs.
Für den natürlichen Tag (tib.: nyin zhag) mit 24 Stunden ergibt dies folgendes:
| Tibetische Bezeichnung: | nyin zhag | chu tshod | chu srang | dbugs | |||||
|---|---|---|---|---|---|---|---|---|---|
| Bedeutung: | Natürlicher Tag | Tibetische Stunde | Tibetische Minute | Atemzug | |||||
| Umrechnungsfaktor zur nächsthöheren Einheit: | 60 | 60 | 6 | ||||||
| Länge: | 24 Stunden | 24 Minuten | 24 Sekunden | 4 Sekunden |
Literatur
- David P Jackson, Janice Jackson: Tibetan Thangka Painting. Methods & Materials. Second and Revised Edition. London 1988
- Loden Sherab Dagyab: Tibetan Religious Art. Part I-II. Wiesbaden 1977
- Winfried Petri: Indo-tibetische Astronomie. Habilitationsschrift zur Erlangung der venia legendi für das Fach Geschichte der Naturwissenschaften an der Hohen Naturwissenschaftlichen Fakultät der Ludwig Maximilians Universität zu München. München 1966
- Dieter Schuh: Untersuchungen zur Geschichte der Tibetischen Kalenderrechnung. Wiesbaden 1973
- Dieter Schuh: Studien zur Geschichte der Mathematik und Astronomie in Tibet, Teil 1, Elementare Arithmetik. Zentralasiatische Studien des Seminars für Sprach- und Kulturwissenschaft Zentralasiens der Universität Bonn, 4, 1970, S. 81–181
- Ngag-dbang chos-'byor: rDe'u'i rtsis-rig la mkho-re'i byis-pa mgu-ba'i long-gtam. Alter tibetischer Blockdruck einer Abhandlung, verfasst von einem Beamten des Schatzamtes des Klosters Trashilhünpo.
Einzelnachweise
- Precious Deposits, Vol. Four, Beijing 2000, S. 272
- Aufgrund eines armenischen Händlertagebuchs aus dem Ende des 17. Jahrhunderts macht Levon Khachikian folgende Angaben zu den damaligen in Lhasa benutzten Gewichtseinheiten für Gold: 20 seva = 1 sookam (zho gang?). 1 sookam = 12 kal, was 5.06 g entspricht. Vgl. Khachikian, Levon: "The Ledger of the Merchant Hovhannes Joughayetsi". Journal of the Asiatic Society, vol 8, no 3, 1966, p. 153–186.