Tesseral
Als tesseral werden mathematische Funktionen bezeichnet, mit denen man Phänomene auf einer Fläche beschreiben kann, die einen schachbrett-artigen Verlauf besitzen.
Kugelflächenfunktionen bzw. Massefunktionen
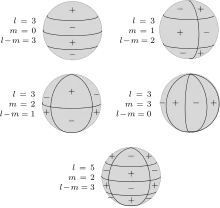
oben zonal,
Mitte sektoriell,
unten tesseral.
In den Geowissenschaften verwendet man tesserale Kugelflächenfunktionen, um sowohl breiten- als auch längenabhängige Erscheinungen rechnerisch zu analysieren. Im Gegensatz dazu werden nur breitenabhängige Terme als zonal bezeichnet, nur längenabhängige als sektoriell. Die dynamische Satellitengeodäsie verwendet seit Anfang der 1970er Jahre tesserale harmonische Funktionen, um die Massefunktionen – die Abweichungen des Erdschwerefeldes von dem eines theoretischen Erdellipsoids – zu beschreiben. In den ersten Jahren der Satellitengeodäsie (1958 bis etwa 1970) war es hingegen nur möglich, zonale Parameter aus den Bahnstörungen der Satelliten abzuleiten.
Der größte zonale Parameter J2 (der in neuerer Schreibweise von harmonischen Reihenentwicklungen als C{2,0} bezeichnet wird) stellt die Erdabplattung dar, den 21 Kilometer-Unterschied zwischen dem Äquatorradius und dem Polradius der Erde. Die nächstgrößeren Massefunktionen J3 und J4 (in heutigen Reihenentwicklungen als C{3,0} und C{4,0} bezeichnet) machen nur mehr etwa 15 Meter in der Erdfigur aus, während der größte längenabhängige Koeffizient C{2,2} die Elliptizität des Erdäquators beschreibt und etwa 50 Meter Höhenabweichung bedeutet.
Die weiteren tesseralen Terme sind nur mehr im Meter- bis Dezimeter-Bereich und können heute aus Satellitenbahnen bis etwa zur Ordnung 70 berechnet werden (symbolisch C{n,m} und S{n,m}, n=2…70, m=0…n), während sie in Kombination mit terrestrischer Schweremessung bereits bis zur Ordnung n=720 bestimmt werden. Dies entspricht einer mathematischen Beschreibung des (an sich unregelmäßig gekrümmten) Geoids mit einer räumlichen Auflösung von etwa 30 km. Genauere Details müssen durch lokale Messungen bestimmt und „darübergelegt“ werden. Solche Daten erhält man über dem Meer durch Methoden der Satellitenaltimetrie, auf dem Festland durch Gravimetrie oder durch Messung von Lotabweichungen.
Flächenbelegung
Außer den harmonischen Kugelfunktions-Entwicklungen gibt es noch andere Methoden, um tesserale Phänomene auf der Erde zu berechnen. Eine der wichtigsten ist die Methode der Flächenbelegung, die von Karl Rudolf Koch (Universität Bonn) in den 1970er Jahren entwickelt wurde. Hier wird einem quadratischen oder sphärischen Bereich der Erdoberfläche ein konstanter Korrekturwert („Potential der einfachen Schicht“) zugewiesen, der sich an der Grenze zum nächsten Viereck sprunghaft ändert. Infolge dieser Sprungstellen ist die Methode zwar unstetig, kommt aber bei gleicher Auflösung mit wesentlich weniger Parametern aus als die Methoden mit harmonischen Koeffizienten.
Multipole
Eine weitere, relativ oft verwendete Methode ist jene der Multipole, bei der eine beliebige Massenverteilung (z. B. in der tieferen Erdkruste oder im Erdmantel) durch günstig platzierte Massenpunkte angenähert wird. Wesentliche Weiterentwicklungen dieser Methode gehen u. a. auf Bernhard Hofmann-Wellenhof (TU Graz) zurück.
Literatur
- Karl Ledersteger: Astronomische und Physikalische Geodäsie (Erdmessung). JEK. Band V, Kapitel 6, 7 und 12. Metzler, Stuttgart 1968.
- Rudolf Sigl, E.Groten: Dynamische Satellitengeodäsie. Ein Überblick. DGK. Reihe A, Band 49. München 1966.
- Günter Seeber: Satellitengeodäsie. de Gruyter, um 1975 und 1995.
- Manfred Schneider: Himmelsmechanik. In 4 Bänden. Band I und III. München 1995 und 1999.
- Wolfgang Torge: Geodäsie. de Gruyter, Berlin 1975. Englische Ausgabe: Geodesy. 2001.
Weblinks
- Aufgabenbereich Satellitengeodäsie an der Universität Bonn.