Taylor-Couette-Strömung
Taylor-Couette-Strömung bezeichnet die Strömung einer inkompressiblen viskosen Flüssigkeit, die sich im Raum zwischen zwei koaxialen, relativ zueinander rotierenden Zylindern befindet. Die Strömung zwischen den Zylindern ist dabei nicht nur von der Rotationsgeschwindigkeit abhängig, sondern auch davon, ob der innere oder der äußere Zylinder rotiert.
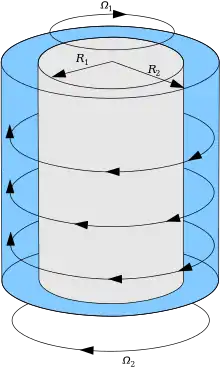
Ist die Relativgeschwindigkeit der Zylinder gering (s. u.) und der Spalt zwischen ihnen klein gegenüber ihren Durchmessern, so kann die Strömung als ebene laminare Strömung behandelt werden (Couette-Strömung). Das Geschwindigkeitsprofil ist ähnlich dem idealisierten Fall einer ebenen Strömung zwischen zwei Platten, von denen die eine relativ zur anderen langsam bewegt wird. Dabei kann eine Platte als feststehend und die andere als bewegt betrachtet werden.
Die Strömung wurde nach Maurice Couette benannt, der Ende des 19. Jahrhunderts das erste funktionierende Rotationsviskosimeter konstruierte und dazu die laminare Grundströmung (Couette-Strömung) nutzte, und nach Geoffrey Ingram Taylor, der die Instabilitäten bei höherer Rotationsgeschwindigkeit untersuchte und theoretisch erklärte.[1] Couette suchte Wirbel zu vermeiden und drehte nur den äußeren Zylinder.[2] Dass dagegen Wirbel bei Drehung des inneren Zylinders entstehen vermutete schon George Stokes 1880, wurde unter anderem durch Henry R. A. Mallock (1888) experimentell gefunden und Rayleigh, dem Lord Kelvin das Phänomen mitteilte, veröffentlichte die grundlegende Erklärung dafür 1916.[3] Ausführlich analysiert wurden sie durch Taylor, dessen Arbeit auch in mehrfacher Hinsicht eine grundlegende Arbeit zur Hydrodynamik war (Bestätigung von Randbedingungen ohne Schlupf in viskosen Flüssigkeiten, Bestätigung der Gültigkeit der Navier-Stokes-Gleichungen, eines der ersten Beispiele linearer Stabilitätsanalyse in der Hydrodynamik).
Entstehung und Wirbelbildung
Rotiert ausschließlich der äußere Zylinder, so verhält sich die Strömung entsprechend der naiven Erwartung: es bildet sich eine gleichmäßige laminare Strömung zwischen den beiden Zylindern. Dieses intuitiv zugängliche Bild bleibt auch dann erhalten, wenn sich der innere Zylinder langsam dreht.
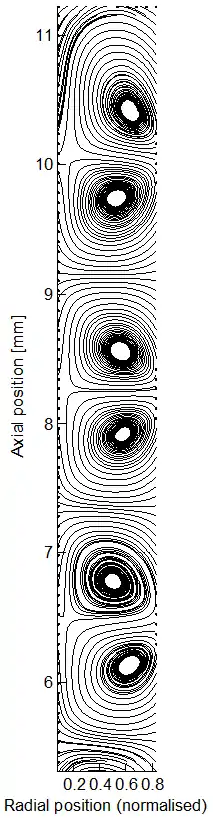
Bei höheren Geschwindigkeiten des inneren Zylinders jedoch zerfällt die Strömung in Streifen, da die durch die Zentrifugalkraft beschleunigte Flüssigkeit am inneren Zylinder nach außen drängt; hierdurch entstehen Taylor-Wirbel, die senkrecht zur Rotationsachse stehen. Typische Wellenlängen der Wirbel sind 2 d (mit d der Spaltlänge zwischen den Zylindern). Die Entstehungsbedingungen der Wirbel werden durch die Taylor-Zahl charakterisiert. Nach Taylor (1923) entstehen Wirbel, falls die Reynolds-Zahl
wobei v die Umfangsgeschwindigkeit, die kinematische Viskosität, d der Spaltabstand und r der mittlere Radius ist. Turbulenz entsteht erst bei wesentlich höheren Geschwindigkeiten (Faktor 50).[4] Typischerweise rotiert der innere Zylinder. Die Wirbel haben Torus-Form und sind längs der Drehachse angeordnet, wobei sich die Drehrichtung abwechselt.
Bei einer weiteren Erhöhung der Rotationsgeschwindigkeit des inneren Zylinders entstehen komplexere Wellenformen die schließlich in Turbulenz übergehen. Die Taylor-Couette-Strömung diente deshalb auch zur Untersuchung von Übergangsszenarien in das Chaotische Regime, zum Beispiel in klassischen Experimenten von Harry Swinney und Jerry Gollub.[5]
 Taylor-Instabilitäten mit zunehmender Reynoldszahl
Taylor-Instabilitäten mit zunehmender Reynoldszahl Taylor-Wirbel zwischen Zylinderwänden, sichtbar gemacht mit Farbbeimischung
Taylor-Wirbel zwischen Zylinderwänden, sichtbar gemacht mit Farbbeimischung
Anwendungsbeispiel
%252C_animiert.gif)
Schlammentwässerung[6] ist ein Verfahrensschritt in Industrie und kommunalen Klärwerken. Zur optimalen Entwässerung in den Entwässerungsaggregaten ist eine Flockenbildung der Schlamminhaltsstoffe über die Beimischung von Flockungshilfsmitteln eine Vorbedingung. Die sich bildenden Flocken sind nicht besonders scherstabil. Zur Verbesserung der Stabilität kommt ein Verfahren zum Einsatz, dessen physikalische Grundlage die Taylor-Couette-Strömung ist. Der mit Flockungshilfsmitteln versetzte Schlamm durchläuft ein Aggregat, das man als „mechanischen Flockenformer“ bezeichnet.
Die Festphase in einer Suspension weicht grundsätzlich in Richtung eines abnehmenden Gradienten der Scherströmung aus, in einer Taylor-Couette-Strömung also ins Innere der Taylorwirbel. Dort findet nur noch ein stetiges Rollen der entstehenden, groben Flocken statt, bis sie am Ende der Wirbelstrecke (s. Bild) unzerstört freigegeben werden. Durch die Absetzbewegung der gröberen Partikel in die Wirbel hinein werden auch Feinstschwebstoffe in den Peletts gebunden und gehen anschließend mit dem Feststoff ab.
Das nachfolgende Entwässerungsaggregat kann den Trennprozess anschließend schneller und mit besserer Trennschärfe ausführen. Die Zuführung der Flockungshilfsmittel kann damit sparsamer erfolgen.
Literatur
- Pascal Chossat, Gérard Iooss: The Couette–Taylor Problem (= Applied Mathematical Sciences. 102). Springer, New York NY u. a. 1994, ISBN 0-387-94154-1.
- Russell J. Donnelly: Taylor-Couette flow: The early days. In: Physics Today. Bd. 44, Nr. 11, 1991, S. 32–39, doi:10.1063/1.881296.
- E. L. Koschmieder: Bénard Cells and Taylor Vortices. Cambridge University Press, Cambridge u. a. 1993, ISBN 0-521-40204-2.
- Richard Lueptow: Taylor-Couette Flow. In: Scholarpedia. Bd. 4, Nr. 11, 2009, 6389, doi:10.4249/scholarpedia.6389.
- Herbert Oertel (Hrsg.): Prandtl-Führer durch die Strömungslehre. 10., vollständig überarbeitete Auflage. Vieweg, Braunschweig u. a. 2002, ISBN 3-528-38209-0.
Weblinks
Einzelnachweise
- Geoffrey I. Taylor: Stability of a Viscous Liquid contained between Two Rotating Cylinders. In: Philosophical Transactions of the Royal Society. Series A: Mathematical, Physical and Engineering Sciences. Bd. 223, 1923, S. 289–343, doi:10.1098/rsta.1923.0008.
- Maurice Couette: Études sur le frottement des liquides. In: Annales de Chimie et de Physique. Série 6, Bd. 21, 1890, S. 433–510.
- Lord Rayleigh: On the dynamics of revolving fluids In: Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences. Bd. 93, Nr. 648, 1916, S. 148–154, JSTOR 93794.
- Ludwig Prandtl, Klaus Oswatitsch, Karl Wieghardt: Führer durch die Strömungslehre. 9., verbesserte und erweiterte Auflage. Vieweg, Braunschweig 1990, ISBN 3-528-28209-6, S. 189.
- Jerry P. Gollub, Harry L. Swinney: Onset of Turbulence in a Rotating Fluid. In: Physical Review Letters. Bd. 35, Nr. 14, 1975, 927–930, doi:10.1103/PhysRevLett.35.927.
- Eine Anwendung des Taylor-Couette-Strömungsprinzips in der Schlammentwässerung (Memento des Originals vom 21. Februar 2016 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis. (PDF; 688 kB).