Taguchi-Methode

Die Taguchi-Methode, benannt nach ihrem Erfinder Taguchi Gen’ichi (anglisiert: Genichi Taguchi), ist eine Versuchsmethode, die vor allem auf die Minimierung der Streuung um den Sollwert abzielt. Die Taguchi-Methode versucht, dieses Ziel dadurch zu erreichen, dass Produkte, Prozesse und Systeme möglichst robust gestaltet werden. Damit ist gemeint, dass sie möglichst unempfindlich gegenüber Störeinflüssen (engl. noise) sein sollen, denen sie in der Praxis ausgesetzt sein werden.

Anwendung findet die Taguchi-Methode im Qualitätsmanagement und in Six Sigma.

Die Verlustfunktion

Statt geforderte Toleranzen als bei der Fertigung einzuhaltende Grenzwerte zu betrachten, wertet die Taguchi-Methode jede Abweichung vom Sollwert (auch innerhalb der Toleranzgrenzen) als einen Fehler, der einen konkreten finanziellen Verlust verursacht. Dieser finanzielle Verlust wird im Rahmen der Taguchi-Methode anhand der so genannten Verlustfunktion modelliert. Mathematisch betrachtet stellt die Verlustfunktion eine Parabel dar. Das heißt, das Modell geht davon aus, dass eine doppelt so große Abweichung vom Sollwert einen viermal so hohen finanziellen Verlust verursacht. Der finanzielle Verlust ist dann minimiert, wenn der erreichte Wert genau dem Sollwert entspricht.[1]

Taguchis Verlustkonzept beschränkt sich nicht auf den finanziellen Verlust, der dem Hersteller entsteht, wenn er ein schlechtes Produkt produziert. Vielmehr modelliert die Verlustfunktion den Verlust, der der Gesellschaft entsteht, wenn ein Konsument ein Produkt verwendet, dessen Merkmale ihre Sollwerte nicht einhalten.[2] Die Idee, den Verlust für die Gesellschaft statt den Verlust für das eigene Unternehmen zu minimieren, stellt einen Bruch mit der traditionellen Denkweise dar.[1]

L(y)=K(y-T)^{2}

$L$ = Qualitätsverlust, $y$ = tatsächlich gemessener Wert, $T$ = Sollwert, $K$ = Geschätzter Geldwert, der mit der Abweichung vom Sollwert in Verbindung steht

Signal-Störgrößen-Verhältnis und Robustheitsmaß

Als Maß für die Streuung um den Sollwert wird, dem Vorschlag Taguchis folgend, das so genannte Signal-Störgrößen-Verhältnis verwendet, das dem Signal-Rausch-Verhältnis (engl. signal to noise ratio) der Fernmeldetechnik (Taguchi arbeitete einmal in diesem Bereich) nachempfunden ist.[3] Dafür schreibt man auch kurz S/N-Verhältnis.

{\frac {S}{N}}=10\log _{10}\left({\frac {{\bar {Y}}^{2}}{s^{2}}}\right)

mit $S$ = Effekt des Signals, $N$ = Effekt der Störgrößen („Rauschen“), ${\bar {Y}}$ = Mittelwert der Zielgröße und $s$ = Standardabweichung[4]

Da das S/N-Verhältnis den Mittelwert ${\bar {Y}}$ der Zielgröße beinhaltet, ist es somit auch von deren Mittelwertlage abhängig. Bei Parametern, bei denen die Standardabweichung aufgrund physikalischer Zusammenhänge im Gleichschritt mit dem Mittelwert ansteigt, ist dies sinnvoll. Interessiert jedoch nur die Standardabweichung, unabhängig vom Mittelwert, so reicht statt des S/N-Verhältnisses das Robustheitsmaß zur Beurteilung des Prozesses bzw. Systems aus. Die Robustheit berechnet sich dann laut folgender Formel:

{\text{Robustheit}}=10\log _{10}\left({\frac {1}{s^{2}}}\right)

Diese S/N-Formeln gelten für Merkmale, die einen festgelegten Sollwert haben. Bei Merkmalen, die im Idealfall möglichst große bzw. möglichst kleine Werte annehmen sollten, verwendet Taguchi andere S/N-Berechnungsformeln.

Die Taguchi-Entwicklungsphilosophie

Taguchi teilt den Entwicklungsprozess in drei Schritte ein:[5]

Systemdesign
Parameterdesign
Toleranzdesign

Diese drei Schritte werden von ihm auch als Offline-Qualitätslenkung (engl. offline quality control) bezeichnet. Jeder dieser Schritte hat seine eigene Funktion:

Im Systemdesign entscheiden die Konstrukteure, was für eine Art von System gebaut werden soll, also zum Beispiel welche Technologie verwendet werden soll, aus welchen Komponenten das System bestehen soll usw.[5]

Im Parameterdesign geht es darum, alle Parameter des Designs (Steuergrößen, Faktoren) so zu optimieren, dass das System möglichst unempfindlich gegenüber Störeinflüssen wird. Das heißt, es werden ideale Sollwerte für die verschiedenen Parameter bestimmt. Hierzu werden statistische Versuchsplanungsmethoden eingesetzt.[5]

Im Toleranzdesign werden die Toleranzen für die Systemparameter festgelegt. Auch hierzu werden statistische Versuchsplanungsmethoden eingesetzt. Ziel ist, die Toleranzen gemäß der tatsächlichen Auswirkung der Parameter auf die Funktion des Systems festzulegen. Wenn ein Faktor nachweislich keinen großen Einfluss auf die Funktion hat, wird eine breite Toleranz festgelegt. Dies spart Fertigungskosten.[5]

Taguchi-Versuchspläne

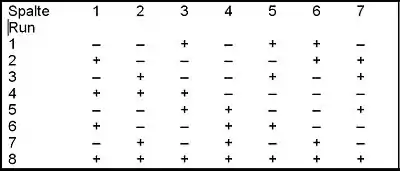
Das orthogonale Feld L₈ (2³). Die Versuchsfaktoren werden den sieben Spalten zugeordnet. Plus und Minus stehen für die beiden untersuchten Stufen des Faktors (Beispiel: Faktor Temperatur; „+“ steht dann für den hohen Temperaturwert, „–“ für den niedrigen). Die Zeilen entsprechen den Versuchsläufen und geben vor, auf welche seiner beiden Stufen jeder der Faktoren in dem betreffenden Versuchslauf gestellt werden muss.

Versuchspläne nach Taguchi sind im Wesentlichen Teilfaktorpläne (engl. fractional factorial designs), das heißt, es werden nicht alle möglichen Kombinationen von Faktorstufen durchgespielt, sondern nur eine genau ausgewählte Teilmenge. Zur Erstellung der Versuchspläne werden so genannte orthogonale Felder (engl. orthogonal arrays) herangezogen, die in Nachschlagewerken vertafelt sind.[6]

Taguchi-Versuchspläne zur Parameteroptimierung beinhalten oft ein inneres und ein äußeres Feld; im inneren Feld stehen die Steuergrößen (vom Ingenieur frei gestaltbare Konstruktionsparameter), und im äußeren Feld die Störgrößen (Umweltfaktoren usw., die in der Praxis unvermeidbaren und unbeeinflussbaren Schwankungen unterworfen sind und dadurch einen Einfluss auf das Prozessergebnis haben).[4] Das äußere Feld (engl. outer array) ist dabei in der Regel wesentlich kleiner als das innere (engl. inner array). Wenn das äußere Feld zum Beispiel vier Versuchsläufe umfasst, muss jeder der Versuchsläufe des inneren Feldes viermal gefahren werden, einmal bei jeder im äußeren Feld vorgesehenen Kombination von Störgrößenstufen.

Das Ziel ist es, die Kombinationen von Steuergrößenstufen zu finden, bei denen die Auswirkungen der Störgrößen minimiert sind und gleichzeitig auch der gewünschte Sollwert eingehalten wird.[5]

Die Auswertung der Versuche erfolgt in drei Schritten, die der Tatsache Rechnung tragen, dass die Einregelung auf den Sollwert im Allgemeinen wesentlich einfacher zu erreichen ist als die Minimierung der Streuung:

Faktoren mit dem größten Einfluss auf das S/N-Verhältnis identifizieren.
Diese Faktoren auf die Stufen stellen, die eine maximale Unempfindlichkeit gegenüber den Störgrößen sicherstellen (Minimierung der Streuung).
Einregeln des Mittelwerts auf den Sollwert anhand der restlichen Faktoren, die das S/N-Verhältnis nicht oder nur geringfügig beeinflussen.

Rezeption

Taguchis auf Robustheit zielende Qualitätsphilosophie, verknüpft mit dem Einsatz statistischer Versuchsplanungsmethoden als Mittel zur Verwirklichung dieses Ziels, hat in der Industrie sehr breite Anerkennung gefunden. Die von ihm verwendeten statistischen Methoden sind jedoch zum Teil als unnötig kompliziert, ineffizient, unsachgemäß oder verbesserungswürdig beurteilt worden.[7] Ansatzpunkte für Kritik sind u. a. die Formeln für das S/N-Verhältnis, die mangelnde statistische Effizienz der aus einem inneren und einem äußeren Feld zusammengesetzten Versuchspläne und die aus der Anwendung von Teilfaktorplänen resultierende Gefahr von Vermengungen zwischen Haupt- und Wechselwirkungen.[8]

Literatur

Wilhelm Kleppmann: Versuchsplanung. Produkte und Prozesse optimieren. 7. aktualisierte und erweiterte Auflage. Hanser, München u. a. 2011, ISBN 978-3-446-42774-7 (Praxisreihe Qualitätswissen).

Einzelnachweise

D. C. Montgomery: Design and Analysis of Experiments. John Wiley & Sons, New York – Chichester – Brisbane – Toronto – Singapore, 1991, ISBN 0-471-52994-X, S. 416.
Thomas L. Albright, Robert W. Ingram, John W. Hill: Managerial Accounting. Information for Decisions. South-Western, 2006, ISBN 0-324-22242-4, S. 255–262 (englisch).
Dr. J. Krottmaier, Versuchsplanung, Verlag Industrielle Organisation Zürich/Verlag TÜV Rheinland, 1991, ISBN 3-88585-812-6 und ISBN 3-85743-945-9, S. 135, S. 186.
D. C. Montgomery: Design and Analysis of Experiments. John Wiley & Sons, New York – Chichester – Brisbane – Toronto – Singapore, 1991, ISBN 0-471-52994-X, S. 418.
D. C. Montgomery: Design and Analysis of Experiments. John Wiley & Sons, New York – Chichester – Brisbane – Toronto – Singapore, 1991, ISBN 0-471-52994-X, S. 415.
D. C. Montgomery: Design and Analysis of Experiments. John Wiley & Sons, New York – Chichester – Brisbane – Toronto – Singapore, 1991, ISBN 0-471-52994-X, S. 421.
G. E. P. Box, S. Bisgaard, C. A. Fung: An Explanation and Critique of Taguchi's Contributions to Quality Engineering. In: Quality and Reliability Engineering International, Vol. 4, S. 123–131.
D. C. Montgomery: Design and Analysis of Experiments. John Wiley & Sons, New York – Chichester – Brisbane – Toronto – Singapore, 1991, ISBN 0-471-52994-X, S. 414–433.

Weblinks

Taguchi-Methoden auf Versuchsmethoden.de

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[DCM416-1] D. C. Montgomery: Design and Analysis of Experiments. John Wiley & Sons, New York – Chichester – Brisbane – Toronto – Singapore, 1991, ISBN 0-471-52994-X, S. 416.

[2] Thomas L. Albright, Robert W. Ingram, John W. Hill: Managerial Accounting. Information for Decisions. South-Western, 2006, ISBN 0-324-22242-4, S. 255–262 (englisch).

[3] Dr. J. Krottmaier, Versuchsplanung, Verlag Industrielle Organisation Zürich/Verlag TÜV Rheinland, 1991, ISBN 3-88585-812-6 und ISBN 3-85743-945-9, S. 135, S. 186.

[DCM418-4] D. C. Montgomery: Design and Analysis of Experiments. John Wiley & Sons, New York – Chichester – Brisbane – Toronto – Singapore, 1991, ISBN 0-471-52994-X, S. 418.

[DCM415-5] D. C. Montgomery: Design and Analysis of Experiments. John Wiley & Sons, New York – Chichester – Brisbane – Toronto – Singapore, 1991, ISBN 0-471-52994-X, S. 415.

[DCM421-6] D. C. Montgomery: Design and Analysis of Experiments. John Wiley & Sons, New York – Chichester – Brisbane – Toronto – Singapore, 1991, ISBN 0-471-52994-X, S. 421.

[7] G. E. P. Box, S. Bisgaard, C. A. Fung: An Explanation and Critique of Taguchi's Contributions to Quality Engineering. In: Quality and Reliability Engineering International, Vol. 4, S. 123–131.

[DCM414-433-8] D. C. Montgomery: Design and Analysis of Experiments. John Wiley & Sons, New York – Chichester – Brisbane – Toronto – Singapore, 1991, ISBN 0-471-52994-X, S. 414–433.