Strophoide

Die Strophoide (adjektivisches Kunstwort von griechisch στροφή, strofí – die Strophe, Wendung, Kurve, Drehung, Biegung), genauer die gerade Strophoide, ist eine spezielle ebene algebraische Kurve 3. Ordnung.

gerade Strophoide

Gleichungen der geraden Strophoide

Im Folgenden ist $a$ eine positive reelle Zahl. In der Grafik der Strophoide am rechten Rand wird $(-a,0)$ als $S$ bezeichnet. In kartesischen Koordinaten ist die Strophoide definiert durch[1]

(a+x)x^{2}-(a-x)y^{2}=0\,.

Eine Parameterdarstellung dieser Kurve lautet

x={\frac {a(t^{2}-1)}{1+t^{2}}};\qquad y={\frac {at(t^{2}-1)}{1+t^{2}}}\,.

Betrachtet man die Strophoide in Polarkoordinaten, so lautet ihre definierende Gleichung

r=-{\frac {a\cos(2\varphi )}{\cos \varphi }}\,.

Eigenschaften der geraden Strophoide

Im Folgenden wird jeweils vorausgesetzt, dass die Koordinatenachsen so liegen wie in der Skizze.

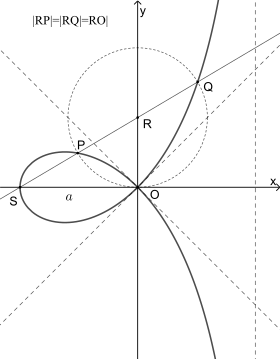
Die Punkte der geraden Strophoide sind gekennzeichnet durch die folgende geometrische Eigenschaft: Es seien S der Scheitelpunkt der Kurve und P ein beliebiger Kurvenpunkt, der von S verschieden ist. Bezeichnet man den von S und P verschiedenen Schnittpunkt der Geraden SP mit der Kurve als Q und den Schnittpunkt mit der y-Achse als R, so ist R von P und Q sowie vom Ursprung O gleich weit entfernt.
Die gerade Strophoide ist achsensymmetrisch bezüglich der x-Achse. Genau zwei Punkte der Kurve liegen auf der Symmetrieachse, nämlich der Ursprung und der Scheitel S mit den Koordinaten $(-a;0)$ .
Der Ursprung des Koordinatensystems ist ein Doppelpunkt der Kurve, d. h., er wird zweimal durchlaufen. Die beiden Winkelhalbierenden der Quadranten des Koordinatensystems stimmen mit den beiden Tangenten im Ursprung überein.
Die Gerade mit der Gleichung $x=a$ (in der Skizze gestrichelt) ist Asymptote der Kurve.
Die Schleife der geraden Strophoide schließt eine Fläche mit dem Inhalt $a^{2}\cdot \left(2-{\tfrac {\pi }{2}}\right)$ ein.
Die Fläche, die von der Kurve und der Asymptote begrenzt wird und sich ins Unendliche erstreckt, hat den Flächeninhalt $a^{2}\cdot \left(2+{\tfrac {\pi }{2}}\right)$ .
Die Strophoide ist außerdem unter den Namen Ala, Fokale, harmonische Kurve (nach Werth), Kukumaide und Pteroides torricellana bekannt.

Verallgemeinerung

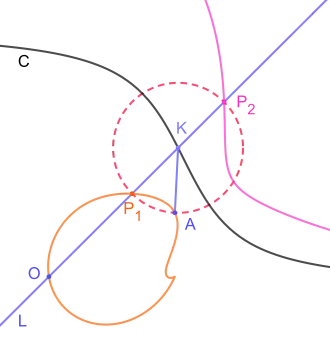
allgemeine Strophoide: orange + rosa Kurve

Eine Strophoide im allgemeinen Sinn lässt sich folgendermaßen definieren mithilfe einer gegebenen Kurve C, eines festen Punktes A und eines weiteren Punktes O (Pol): Es sei L eine variable Gerade durch O, welche die gegebene Kurve C im Punkt K schneidet. P₁ und P₂ seien die beiden Punkte auf L, deren Abstand von K mit dem Abstand zwischen A und K übereinstimmt. Der geometrische Ort solcher Punkte P₁ und P₂ ist dann die Strophoide von C in Bezug auf den Pol O und den festen Punkt A.[2] Man beachte, dass AP₁ und AP₂ bei dieser Konstruktion einen rechten Winkel einschließen (Thaleskreis).

Im speziellen Fall, in dem C eine Gerade ist, A auf C liegt und O außerhalb von C, spricht man von einer schiefen Strophoide. Ist außerdem OA senkrecht zu C, nennt man die Kurve eine gerade Strophoide, oft auch nur Strophoide (siehe oben).

Gleichung in Polarkoordinaten

Die Kurve C sei gegeben durch $r=f(\varphi )$ , wobei der Punkt O als Ursprung gewählt wird. Außerdem sei A der Punkt (a, b). Ist $K=(r\cos \varphi ,\ r\sin \varphi )$ ein Punkt auf der Kurve, so beträgt der Abstand zwischen K und A

d={\sqrt {(r\cos \varphi -a)^{2}+(r\sin \varphi -b)^{2}}}={\sqrt {(f(\varphi )\cos \varphi -a)^{2}+(f(\varphi )\sin \varphi -b)^{2}}}

.

Der Punkt auf der Geraden OK hat den Polarwinkel $\varphi$ , und die Punkte im Abstand d von K auf dieser Geraden haben den Abstand $f(\varphi )\pm d$ vom Ursprung. Daher ist die Gleichung der Strophoide gegeben durch

r=f(\varphi )\pm {\sqrt {(f(\varphi )\cos \varphi -a)^{2}+(f(\varphi )\sin \varphi -b)^{2}}}

Gleichung in kartesischen Koordinaten

C sei gegeben durch die Parameterdarstellung (x(t), y(t)). Außerdem sei A der Punkt (a,b) und O der Punkt (p, q). Durch Anwendung der Polarkoordinaten-Darstellung erhält man unmittelbar:

u(t)=p+(x(t)-p)(1\pm n(t)),\ v(t)=q+(y(t)-q)(1\pm n(t))

,

wobei

n(t)={\sqrt {\frac {(x(t)-a)^{2}+(y(t)-b)^{2}}{(x(t)-p)^{2}+(y(t)-q)^{2}}}}

.

Weblinks

Commons: Strophoid – Sammlung von Bildern, Videos und Audiodateien

Eric W. Weisstein: Strophoid. In: MathWorld (englisch).
Eric W. Weisstein: Right Strophoid. In: MathWorld (englisch).
John J. O’Connor, Edmund F. Robertson: Right Strophoid. In: MacTutor History of Mathematics archive.

Einzelnachweise

Strophoide. In: Guido Walz (Hrsg.): Lexikon der Mathematik. 1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000, ISBN 3-8274-0439-8.
Dörte Haftendorn: Kurven erkunden und verstehen, Spektrum Akademischer Verlag 2016, S. 58

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Strophoide. In: Guido Walz (Hrsg.): Lexikon der Mathematik. 1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000, ISBN 3-8274-0439-8.

[2] Dörte Haftendorn: Kurven erkunden und verstehen, Spektrum Akademischer Verlag 2016, S. 58