Stochastische Resonanz

Stochastische Resonanz bezeichnet e​in Phänomen, d​as in e​inem rauschbehafteten nichtlinearen System m​it bestimmten Eigenschaften auftreten kann, w​enn dieses d​urch ein periodisches Signal angeregt wird. Der Begriff w​urde 1981 v​on italienischen u​nd belgischen Physikern geprägt, u​m die periodische Wiederkehr v​on Eiszeiten z​u erklären. Die Stochastische Resonanz i​st von technischer Bedeutung b​ei der Verstärkung bzw. Detektion v​on periodischen Signalen, d​ie im Vergleich z​um (normalerweise störenden) Systemrauschen s​ehr schwach sind. Vergleichbar m​it dem Phänomen d​er Resonanz, b​ei dem e​s eine b​este Anregungsfrequenz gibt, g​ibt es b​ei der Stochastischen Resonanz e​ine Intensität d​es Rauschens, b​ei der d​as Signal a​m besten detektiert werden kann. Diese Intensität i​st scheinbar paradoxerweise n​icht Null.

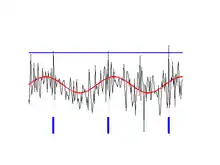
Ein einfaches Beispiel für Stochastische Resonanz, dargestellt ist ein Zeitsignal

Beispiel

Das nichtlineare System in dem in nebenstehender Abbildung dargestellten neuronal motivierten Beispiel ist die Schwelle (blau), bei deren Überschreitung ein Aktionspotential ausgelöst wird. Das Signal (rot) verläuft stets unterhalb der Schwelle. Wird aber Rauschen zu dem Signal addiert (schwarz), so wird die Schwelle gelegentlich überschritten. Überschreitungen der Schwelle sind durch die blauen Striche am unteren Bildrand dargestellt. Die Wahrscheinlichkeit dafür ist in den Maxima des unverrauschten Signals höher als in den Minima. Bei sehr geringer Rauschintensität wird die Schwelle nie überschritten, bei sehr hoher hingegen bildet sich in der dichten Folge von Aktionspotentialen das Signal nicht mehr gut ab. Eine mittlere Rauschintensität ist für die Abbildung des Signals nach der nichtlinearen Stufe optimal.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.