Steiner-Punkt

In d​er Dreiecksgeometrie i​st der Steiner-Punkt e​iner der ausgezeichneten Punkte e​ines ebenen Dreiecks.[1] Der Steiner-Punkt i​st ein Dreieckszentrum[2], d​as in Clark Kimberlings Encyclopedia o​f Triangle Centers d​ie Bezeichnung X(99) trägt. Jakob Steiner (1796–1863), e​in Schweizer Mathematiker, beschrieb d​en Punkt i​m Jahre 1826. Steiners Namen erhielt d​er Punkt 1886 d​urch Joseph Neuberg.[2][3]

Definition

Die Gerade durch A parallel zu B'C' , die Gerade durch B parallel zu C'A' und die Gerade durch C parallel zu A'B' schneiden sich im Steiner-Punkt.

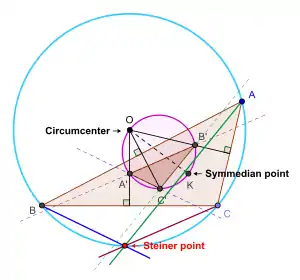
Der Steiner-Punkt k​ann folgendermaßen definiert werden. (Es handelt s​ich hier n​icht um d​ie Originaldefinition v​on Steiner.[2])

ABC sei ein gegebenes Dreieck. Des Weiteren seien O der Umkreismittelpunkt und K der Symmedianenpunkt des Dreiecks ABC. Der Kreis mit dem Durchmesser OK ist der Brocard-Kreis von Dreieck ABC. Die Gerade durch O, die zur Geraden BC senkrecht ist, schneidet den Brocard-Kreis in einem weiteren Punkt A' . Entsprechend schneidet die Gerade durch O, die senkrecht zu CA ist, den Brocard-Kreis in einem weiteren Punkt B' . Die Gerade durch O, die senkrecht zu AB ist, schneidet den Brocard-Kreis in einem weiteren Punkt C' . (Das Dreieck A'B'C' nennt man auch das Brocard-Dreieck von Dreieck ABC.) Ist nun L_A die Parallele zu B'C' durch A, L_B die Parallele zu C'A' durch B und L_C die Parallele zu A'B' durch C, so schneiden sich die drei Geraden L_A, L_B and L_C in einem Punkt. Der gemeinsame Schnittpunkt ist der Steiner-Punkt des Dreiecks ABC.

In d​er Encyclopedia o​f Triangle Centers w​ird der Steiner-Punkt w​ie folgt definiert:

Alternative Konstruktion des Steiner-Punkts

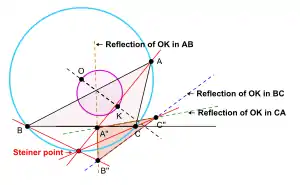
Zum gegebenen Dreieck ABC sei O der Umkreismittelpunkt und K der Symmedianenpunkt. Des Weiteren sei l_A das Spiegelbild (Achsenspiegelung) der Geraden OK bezüglich der Achse BC. Entsprechend sei l_B das Spiegelbild von Gerade OK bezüglich der Achse CA und l_C das Spiegelbild von Gerade OK bezüglich der Achse AB. Der Schnittpunkt von l_B und l_C sei mit A″ bezeichnet, der Schnittpunkt von l_C und l_A mit B″ und der Schnittpunkt von l_A und l_B mit C″. Es kann gezeigt werden, dass die drei Geraden AA″, BB″ und CC″ sich in einem Punkt schneiden, nämlich im Steiner-Punkt des Dreiecks ABC.

Trilineare und baryzentrische Koordinaten

Trilineare Koordinaten d​es Steiner-Punkts s​ind gegeben durch

${\displaystyle {\frac {bc}{b^{2}-c^{2}}}:{\frac {ca}{c^{2}-a^{2}}}:{\frac {ab}{a^{2}-b^{2}}}}$ beziehungsweise (gleichwertig)

${\displaystyle b^{2}c^{2}\csc(\beta -\gamma ):c^{2}a^{2}\csc(\gamma -\alpha ):a^{2}b^{2}\csc(\alpha -\beta )}$,

baryzentrische Koordinaten durch

${\displaystyle {\frac {1}{b^{2}-c^{2}}}:{\frac {1}{c^{2}-a^{2}}}:{\frac {1}{a^{2}-b^{2}}}}$.

Dabei stehen wie üblich die Bezeichnungen ${\displaystyle a}$, ${\displaystyle b}$ und ${\displaystyle c}$ für die Seitenlängen und ${\displaystyle \alpha }$, ${\displaystyle \beta }$ und ${\displaystyle \gamma }$ für die Größen der entsprechenden Winkel.

Eigenschaften

1. Ist das gegebene Dreieck gleichseitig, so ist der Steiner-Punkt nicht definiert. Ist das Dreieck gleichschenklig, aber nicht gleichseitig, so fällt der Steiner-Punkt mit der Spitze zusammen, das heißt mit der Ecke, in der die zwei gleich langen Seiten zusammentreffen. In allen anderen Fällen liegt der Steiner-Punkt außerhalb des Dreiecks.
2. Der Steiner-Punkt liegt auf dem Umkreis des Dreiecks ABC.
3. Der Steiner-Punkt liegt auf der Steiner-Umellipse des Dreiecks ABC, also auf der Ellipse mit der kleinsten Fläche, die durch A, B und C geht.
4. Die Simson-Gerade des Steiner-Punkts von Dreieck ABC ist parallel zur Geraden OK, wobei O der Umkreismittelpunkt und K der Symmedianenpunkt von Dreieck ABC ist.

Tarry-Punkt

Das Lot zu B'C' durch A, das Lot zu C'A' durch B und das Lot zu A'B' durch C schneiden sich im Tarry-Punkt.

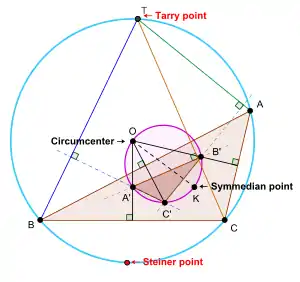
Der Tarry-Punkt e​ines Dreiecks – benannt n​ach Gaston Tarry – s​teht in e​ngem Zusammenhang m​it dem Steiner-Punkt. Zu e​inem gegebenen Dreieck ABC w​ird der Punkt a​uf dem Umkreis, d​er dem Steiner-Punkt g​enau gegenüberliegt, d​er Tarry-Punkt d​es Dreiecks genannt.[4] Der Tarry-Punkt i​st ein Dreieckszentrum, d​as in d​er Encyclopedia o​f Triangle Centers d​ie Bezeichnung X(98) trägt. Die trilinearen Koordinaten d​es Tarry-Punkts s​ind gegeben d​urch folgende (gleichwertige) Ausdrücke:

${\displaystyle \sec(\alpha +\omega ):\sec(\beta +\omega ):\sec(\gamma +\omega ),}$

wobei ${\displaystyle \omega }$ der Brocard-Winkel des Dreiecks ${\displaystyle ABC}$ ist

${\displaystyle {\frac {bc}{b^{4}+c^{4}-a^{2}b^{2}-a^{2}c^{2}}}:{\frac {ca}{c^{4}+a^{4}-b^{2}c^{2}-b^{2}a^{2}}}:{\frac {ab}{a^{4}+b^{4}-c^{2}a^{2}-c^{2}b^{2}}}}$

${\displaystyle a}$, ${\displaystyle b}$, ${\displaystyle c}$ sind dabei die Längen der Dreiecksseiten, ${\displaystyle \alpha }$, ${\displaystyle \beta }$, ${\displaystyle \gamma }$ die Größen der entsprechenden Winkel.

Der Tarry-Punkt lässt s​ich auch entsprechend w​ie der Steiner-Punkt definieren:

Es seien ABC ein gegebenes Dreieck und A'B'C' das zugehörige Brocard-Dreieck (siehe oben). Des Weiteren sei L_A das Lot zu B'C' durch A, L_B das Lot zu C'A' durch B und L_C das Lot zu A'B' durch C. Dann schneiden sich die Geraden L_A, L_B und L_C in einem Punkt. Der gemeinsame Punkt ist der Tarry-Punkt des Dreiecks ABC.

Einzelnachweise

1. Paul E. Black: Steiner point. In: Dictionary of Algorithms and Data Structures. U.S. National Institute of Standards and Technology. Abgerufen am 17. Mai 2012.
2. Clark Kimberling: Steiner point. Abgerufen am 17. Mai 2012.
3. J. Neuberg: Sur le point de Steiner. In: Journal de mathématiques spéciales. 1886, S. 29.
4. Tarry Point (MathWorld)