Schulze-Methode
Die Schulze-Methode (nach Markus Schulze) ist ein Wahlverfahren aus der Familie der Vorzugswahlen, mit dem ein einzelner Sieger bestimmt wird. Es ist die derzeit verbreitetste Methode, um Wahlen durchzuführen, bei welchen der Wähler Kandidaten nach Rang ordnet.
Die Schulze-Methode ist eine Condorcet-Methode, d. h., dass sie einen Kandidaten, der im paarweisen Vergleich jeden anderen Kandidaten besiegen würde, als Sieger auswählt, sofern ein solcher existiert.
Markus Schulze hat die Methode 1997 entwickelt. Die ersten Veröffentlichungen datieren von 2003 und 2006.[1][2][3] Verwendet wurde die Schulze-Methode erstmals 2003 (von Software in the Public Interest), 2003 (von Debian) und 2005 (von Gentoo Linux).
Erklärung
Jeder Wähler erhält eine komplette Liste aller Kandidaten. Er reiht die Kandidaten, indem er ihnen Zahlen zuordnet. Eine kleine Zahl ist besser als eine größere, jedoch zählt nur die Reihenfolge. Kandidaten mit gleicher Zahl sind an gleicher Stelle gereiht. Kandidaten ohne Zahl sind gemeinsam an letzter Stelle – so als ob der Wähler ihnen jeweils die größtmögliche Zahl zugeschrieben hätte.
Anzahl der Wähler
Die Anzahl der Wähler, die den Kandidaten dem Kandidaten vorziehen (d. h. die bei eine kleinere Zahl als bei vermerkt haben), wird durch ausgedrückt.
Der Wert von wird aus den Stimmabgaben gezählt
- ist die Zahl der Wähler, die Kandidaten besser als finden.
- ist die Zahl der Wähler, die Kandidaten besser als finden.
Für diese Werte ist es unerheblich, ob noch andere Kandidaten existieren und ob diese besser oder schlechter als und oder zwischen beiden eingestuft werden.
Definition
Die Schulze-Methode ist folgendermaßen definiert:
- Ein Weg (englisch path) vom Kandidaten zum Kandidaten der Stärke ist eine Sequenz von Kandidaten mit den folgenden Eigenschaften:
- , d. h. der Weg beginnt bei .
- , d. h. der Weg endet bei .
- , d. h. jeder Kandidat auf dem Weg gewinnt den paarweisen Vergleich gegen den auf ihn folgenden Kandidaten.
- , d. h. jeder Kandidat auf dem Weg wird gegenüber dem auf ihn folgenden Kandidaten von mindestens Wählern bevorzugt.
- , d. h. wenigstens einer dieser Vergleiche wird von (nur) genau Wählern gestützt.
- Hat ein Weg die Stärke , so werden die Bögen dieses Weges, für die gilt, kritische Siege genannt. Bei ihnen handelt es sich um die schwächsten Siege auf dem Weg.
- , die Stärke des stärksten Weges vom Kandidaten zum Kandidaten , ist der größte Wert, so dass es einen Weg dieser Stärke vom Kandidaten zum Kandidaten gibt. Falls es überhaupt keinen Weg von nach gibt, wird gesetzt.
- Kandidat ist besser als Kandidat genau dann, wenn ist.
- Kandidat ist ein potentieller Sieger genau dann, wenn ist für jeden anderen Kandidaten .
Es lässt sich zeigen, dass die besser-Relation transitiv ist. Es existiert somit stets mindestens ein potentieller Sieger.
Beispiel 1
| 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| 2 | ||||||||
| 3 | ||||||||
| 4 | ||||||||
| 5 | ||||||||
Paarweise Matrix
Tabelle, die jeden Kandidaten mit jedem anderen vergleicht. Die rot markierten Felder werden weiter benutzt. Z. B. wurde Kandidat von Stimmen gegenüber bevorzugt.
| 20 | 26 | 30 | 22 | ||
| 25 | 16 | 33 | 18 | ||
| 19 | 29 | 17 | 24 | ||
| 15 | 12 | 28 | 14 | ||
| 23 | 27 | 21 | 31 |
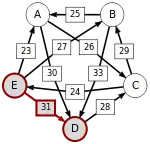
Paarweiser Graph
Graph mit gewichteten Pfeilen aus der Tabelle von oben. Man sieht den Pfeil von Kandidat zu Kandidat mit dem Gewicht von aus der obigen Tabelle.
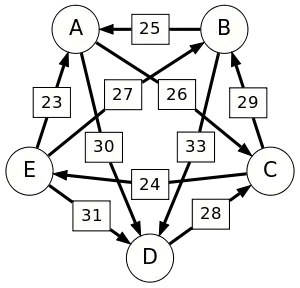
Die stärksten Wege
Von den Verbindungen zwischen Kandidaten wird diejenige gesucht, bei der das schwächste Glied am stärksten ist. Bildlich gesprochen wird die stärkste Kette gesucht. Wie kommt man von nach ?
- Bei über nach ist das schwächste Glied von nach mit .
- Bei über und nach ist das schwächste Glied nach mit . Diese Kette ist stärker und wird nachfolgend verwendet.
Man kann sich den Vorgang beispielsweise aus Sicht eines Transportunternehmens vorstellen, das möglichst viele Pakete auf einmal von einer Stadt in die andere transportieren möchte (egal wie lang der Weg ist). Ohne Zwischenlager kann natürlich nur so viel transportiert werden wie das Fassungsvermögen des kleinsten Transportmittels, das am Weg verwendet wird: Wenn die Pakete zuerst per Fähre, dann per Lastwagen und zuletzt per Güterzug transportiert werden, dann ist wahrscheinlich der Lastwagen am kleinsten. Im Vergleich zu einer anderen Route (die z. B. einen Pickup-Truck enthält) ist der Lastwagen damit das schwächste Glied der stärksten Kette.
Oft wird dieses schwächste Glied der stärksten Kette auch kritischer Sieg genannt. Die kritischen Siege der stärksten Wege sind unterstrichen.
| … nach | … nach | … nach | … nach | … nach | |
| von … | 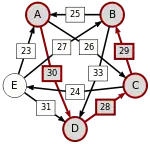 A–(30)–D–(28)–C–(29)–B |
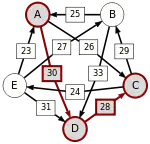 A–(30)–D–(28)–C |
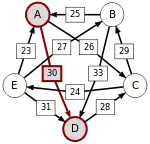 A–(30)–D |
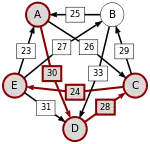 A–(30)–D–(28)–C–(24)–E | |
| von … | 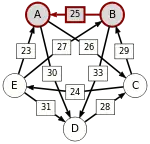 B–(25)–A |
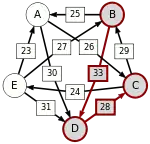 B–(33)–D–(28)–C |
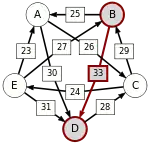 B-(33)-D |
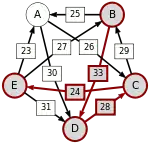 B-(33)-D-(28)-C-(24)-E | |
| von … | 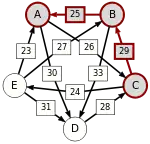 C-(29)-B-(25)-A |
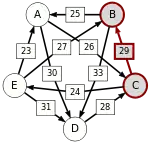 C-(29)-B |
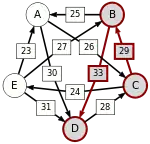 C-(29)-B-(33)-D |
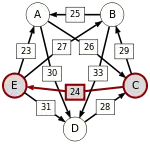 C-(24)-E | |
| von … | 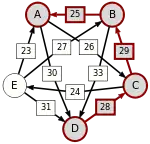 D-(28)-C-(29)-B-(25)-A |
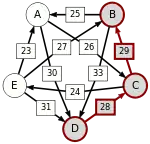 D-(28)-C-(29)-B |
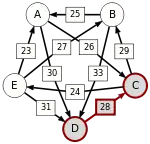 D-(28)-C |
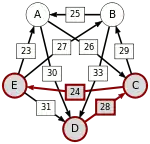 D-(28)-C-(24)-E | |
| von … | 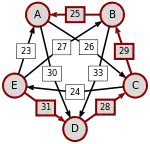 E-(31)-D-(28)-C-(29)-B-(25)-A |
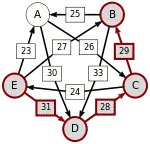 E-(31)-D-(28)-C-(29)-B |
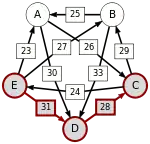 E-(31)-D-(28)-C |
 E-(31)-D |
Die Stärken der stärksten Wege
Das schwächste Glied der stärksten Verbindung, wie oben gefunden, wird in eine Tabelle eingetragen. Dann wird wieder paarweise verglichen, wer wen schlägt, in der Tabelle unten wieder rot markiert.
| 28 | 28 | 30 | 24 | ||
| 25 | 28 | 33 | 24 | ||
| 25 | 29 | 29 | 24 | ||
| 25 | 28 | 28 | 24 | ||
| 25 | 28 | 28 | 31 |
Ergebnis
Sieger nach der Schulze-Methode ist Kandidat , da ist für jeden anderen Kandidaten .
- Wegen ist Kandidat besser als Kandidat .
- Wegen ist Kandidat besser als Kandidat .
- Wegen ist Kandidat besser als Kandidat .
- Wegen ist Kandidat besser als Kandidat .
- Wegen ist Kandidat besser als Kandidat .
- Wegen ist Kandidat besser als Kandidat .
- Wegen ist Kandidat besser als Kandidat .
- Wegen ist Kandidat besser als Kandidat .
- Wegen ist Kandidat besser als Kandidat .
- Wegen ist Kandidat besser als Kandidat .
Das Schulze-Ranking ist somit .
Beispiel 2
| 1 | ||||
|---|---|---|---|---|
| 2 | ||||
| 3 | ||||
| 4 | ||||
Paarweise Matrix
| 5 | 5 | 3 | ||
| 4 | 7 | 5 | ||
| 4 | 2 | 5 | ||
| 6 | 4 | 4 |
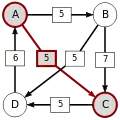
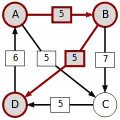
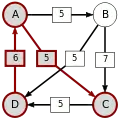
Paarweiser Graph

Die stärksten Wege
Die kritischen Siege der stärksten Wege sind unterstrichen.
| … nach | … nach | … nach | … nach | |
| von … | 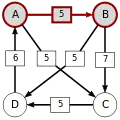 |
 |
 | |
| von … | 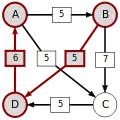 |
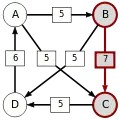 |
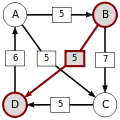 | |
| von … | 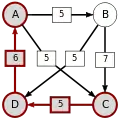 |
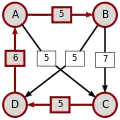 |
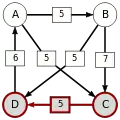 | |
| von … | 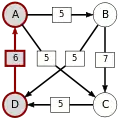 |
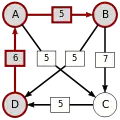 |
 |
Die Stärken der stärksten Wege
Das schwächste Glied der stärksten Verbindung wie oben gefunden, wird in eine Tabelle eingetragen. Dann wird wieder paarweise verglichen, wer wen schlägt, in der Tabelle unten wieder rot markiert. Violett markiert ist jeder Gleichstand.
| 5 | 5 | 5 | ||
| 5 | 7 | 5 | ||
| 5 | 5 | 5 | ||
| 6 | 5 | 5 |
Ergebnis
Potentielle Sieger nach der Schulze-Methode sind somit Kandidat und Kandidat , da
- ist für jeden anderen Kandidaten und
- ist für jeden anderen Kandidaten .
Wegen ist Kandidat besser als Kandidat .
Wegen ist Kandidat besser als Kandidat .
Mögliche Schulze-Rankings sind somit
- ,
- ,
- ,
- ,
- und
- .
Implementierung
Sei C die Anzahl der Kandidaten. Dann lassen sich die Stärken der stärksten Wege mit Hilfe des Algorithmus von Floyd und Warshall berechnen.
Input: d[i,j] ist die Anzahl der Wähler, die den Kandidaten i dem Kandidaten j strikt vorziehen.
Output: p[i,j] ist die Stärke des stärksten Weges vom Kandidaten i zum Kandidaten j.
Beispiel einer Implementierung in Pascal
for i := 1 to C do
begin
for j := 1 to C do
begin
if ( i <> j ) then
begin
if ( d[i,j] > d[j,i] ) then
begin
p[i,j] := d[i,j]
end
else
begin
p[i,j] := 0
end
end
end
end
for i := 1 to C do
begin
for j := 1 to C do
begin
if ( i <> j ) then
begin
for k := 1 to C do
begin
if ( i <> k ) then
begin
if ( j <> k ) then
begin
p[j,k] := max ( p[j,k], min ( p[j,i], p[i,k] ) )
end
end
end
end
end
end
Heuristiken und Eigenschaften
Spezielle Heuristiken der Schulze-Methode sind auch bekannt unter den Namen Beatpath, Beatpaths, Beatpath Method, Beatpath Winner, Path Voting, Path Winner, Schwartz Sequential Dropping (SSD) und Cloneproof Schwartz Sequential Dropping (CSSD).
Die Schulze-Methode erfüllt die folgenden Kriterien[4][5] (Zur Erläuterung der wichtigsten Kriterien siehe Abschnitt Qualitätskriterien im Artikel Sozialwahltheorie):
- Majority criterion
- Mutual majority criterion
- Monotonicity criterion (auch bezeichnet als non-negative responsiveness, mono-raise)
- Pareto criterion
- Condorcet-Kriterium
- Condorcet-Verlierer-Kriterium
- Smith criterion (auch bezeichnet als Generalized Condorcet criterion)
- Local independence from irrelevant alternatives
- Schwartz-Kriterium
- Strategy-Free criterion
- Generalized Strategy-Free criterion
- Strong Defensive Strategy criterion
- Weak Defensive Strategy criterion
- Summability criterion
- Independence of clones
- nicht-diktatorisch
- Universalität
- Woodall’s plurality criterion
- Woodall’s CDTT criterion
- Minimal Defense criterion
- Resolvability
- Reversal symmetry
- mono-append
- mono-add-plump
Die Schulze-Methode verletzt
- das Konsistenzkriterium,
- das Partizipationskriterium,
- die Unabhängigkeit von irrelevanten Alternativen
- sowie das Favorite-betrayal-Kriterium.
Anwendungen
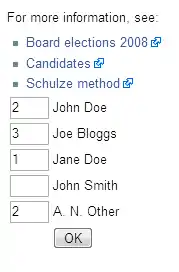
Die Schulze-Methode wird derzeit nicht in staatlichen Wahlen angewandt. Sie findet jedoch mehr und mehr Anwendung in Privatorganisationen. Sie ist u. a. in folgenden Organisationen benutzt worden:
- Wikimedia Foundation[6]
- Piratenpartei Deutschland[7]
- Piratenpartei Schweden[8]
- Piratenpartei Österreichs[9]
- Debian[10]
- Ubuntu[11]
- Software in the Public Interest[12]
- Gentoo Foundation
- Sender Policy Framework[13]
- Free Software Foundation Europe (FSFE)[14]
- KDE[15]
- Kingman Hall[16]
- TopCoder
- GNU Privacy Guard[17]
- Golden Geek Award[18]
- Studierendenrat der Albert-Ludwigs-Universität Freiburg[19]
- Berufsverband der Kinder- und Jugendärzte[20]
- Club der Ehemaligen der Deutschen SchülerAkademien e.V.[21]
Literatur
- Christoph Börgers: Mathematics of Social Choice: Voting, Compensation, and Division. SIAM 2009, ISBN 0-89871-695-0.
- Saul Stahl, Paul E. Johnson: Understanding Modern Mathematics. Jones & Bartlett Publishing, London u. a. 2007, ISBN 0-7637-3401-2, S. 119 ff.
- Nicolaus Tideman: Collective Decisions and Voting: The Potential for Public Choice. Ashgate Publishing, 2006, ISBN 0-7546-4717-X, S. 228 ff.
Weblinks
- Rosa Camps, Xavier Mora, Laia Saumell: A Continuous Rating Method for Preferential Voting. (PDF; 1,76 MB)
- Paul E. Johnson: Voting Systems. (PDF; 324 kB)
- Rob LeGrand: Descriptions of ranked-ballot voting methods.
- Rob Loring: Accurate Democracy.
- James D. McCaffrey: Testlauf: Gruppenentscheidungen bei Softwaretests. MSDN
- Tommi Meskanen, Hannu Nurmi: Distance from Consensus: a Theme and Variations. (PDF; 130 kB) In: Bruno Simeone, Friedrich Pukelsheim (Hrsg.): Mathematics and democracy: recent advances in voting systems and collective choice. Studies in choice and welfare. Springer, Berlin u. a. 2006, ISBN 3-540-35603-7, S. 117–132, hier S. 120 ff.
- Massimo Narizzano, Luca Pulina, Armando Tacchella: Ranking and Reputation Systems in the QBF Competition. (PDF; 455 kB) In: AI*IA ’07 Proceedings of the 10th Congress of the Italian Association for Artificial Intelligence on AI*IA 2007: Artificial Intelligence and Human-Oriented Computing. Springer, Berlin / Heidelberg 2007, ISBN 978-3-540-74781-9.
- Markus Schulze: Schulze-Methode FAQ
- Markus Schulze: A New Monotonic and Clone-Independent Single-Winner Election Method. (PDF; 74 kB) In: Voting Matters, 17, 2003, S. 9–19.
- Kevin Venzke: Election Methods and Criteria.
- Jochen Voss: The Debian Voting System.
- Barry Wright: Objective Measures of Preferential Ballot Voting Systems. (PDF; 289 kB) Abschlussarbeit Duke University, Durham NC 2009.
Einzelnachweise
- Condorcet sub-cycle rule, Election-Methods-Mailingliste, 3. Oktober 1997
- Markus Schulze: A new monotonic and clone-independent single-winner election method. (PDF; 75 kB) In: Voting Matters, issue 17, 2003, S. 9–19
- Nicolaus Tideman: Collective Decisions and Voting: The Potential for Public Choice. Ashgate Publishing, 2006. Saul Stahl, Paul E. Johnson: Understanding Modern Mathematics. Jones & Bartlett Publishing, 2006
- Markus Schulze: A new monotonic, clone-independent, reversal symmetric, and Condorcet-consistent single-winner election method. (PDF; 1,4 MB) Juli 2007 (englisch)
- D. R. Woodall: Properties of Preferential Election Rules. Dezember 1994 (englisch)
- Board election to use preference voting, Mai 2008
- Presseerklärung der Piratenpartei Deutschland (Memento des Originals vom 29. Mai 2011 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis., August 2010
- Probewahl der schwedischen Piraten, Januar 2010
- wiki.piratenpartei.at
- Verfassung für das Debian-Projekt, Anhang A6
- Ubuntu IRC Council Position, Mai 2012
- Process for adding new board members, Januar 2003
- Council Election Procedures (Memento vom 16. Juli 2011 im Internet Archive)
- § 6 Absatz 3 der Satzung (PDF; 112 kB)
- Artikel 3.4.1 der Rules of Procedures for Online Voting
- Kingman adopts Condorcet voting, April 2005
- GnuPG Logo Vote, November 2006 (Memento des Originals vom 16. Dezember 2006 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- Golden Geek Awards
- Geschäftsordnung des Studierendenrats der Albert-Ludwigs-Universität Freiburg. (PDF FDP, 53 kB) In: u-asta.uni-freiburg.de. 13. Mai 2014, abgerufen am 24. Juni 2014.
- Satzung des BVKJ
- § 10 Absatz 3 der Satzung des Clubs der Ehemaligen der Deutschen SchülerAkademien e. V. vom 22.3.2006, zuletzt geändert durch Beschluss vom 14.12.2020, in Verbindung mit § 1 Absatz 3 des Mitgliederbeschlusses zum Abstimmungsverfahren vom 09.12.2013. Quellen abgerufen am: 2021-11-09.