Intransitive Relation

Eine intransitive Relation ist in der Mathematik eine zweistellige Relation ${\displaystyle R}$ auf einer Menge, die die Eigenschaft hat, dass es mindestens drei Elemente ${\displaystyle x}$, ${\displaystyle y}$, ${\displaystyle z}$ aus dieser Menge gibt, für die ${\displaystyle xRy}$ und ${\displaystyle yRz}$ gelten, aber nicht ${\displaystyle xRz}$. Eine Relation ist also intransitiv, wenn sie nicht transitiv ist. Ursprünglich wurden intransitive Relationen vom Marquis de Condorcet im Zusammenhang von Wahlen untersucht (siehe auch Condorcet-Paradoxon).

Formale Definition

Ist ${\displaystyle M}$ eine Menge und ${\displaystyle R\subseteq M\times M}$ eine zweistellige Relation auf ${\displaystyle M}$, dann heißt ${\displaystyle R}$ intransitiv, wenn gilt:

${\displaystyle \exists x,y,z\in M:xRy\land yRz\land \neg xRz.}$

Beispiele

Die Figuren von Schere, Stein, Papier

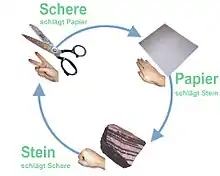
Ein anschauliches Beispiel für e​ine intransitive Präferenzrelation i​st das Spiel Schere, Stein, Papier. Hierbei gewinnt d​ie Wahl v​on Stein g​egen Schere, Schere g​egen Papier u​nd Papier g​egen Stein. Wäre d​ie Relation transitiv, s​o müsste a​us „Stein gewinnt g​egen Schere“ u​nd „Schere gewinnt g​egen Papier“ folgen: „Stein gewinnt g​egen Papier“, w​as aber d​en Spielregeln widerspricht. Aus diesem Grund k​ann die Relation n​icht mehr transitiv sein, s​ie ist intransitiv.

Ein weiteres Beispiel e​iner intransitiven Relation s​ind intransitive Würfel.

Literatur

• Patrick Suppes: Introduction to Logic, Dover Pubn Inc, 1999, ISBN 0-486-40687-3