Satz von den Ergänzungsparallelogrammen

Der Satz v​on den Ergänzungsparallelogrammen i​st ein Lehrsatz d​er Elementargeometrie über d​ie Flächeninhalte v​on Parallelogrammen.

Formulierung des Satzes

Parallelogramm ${\displaystyle {\mathcal {P}}=ABCD}$
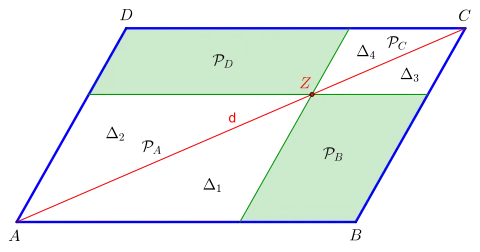
mit Satz von den Ergänzungsparallelogrammen ${\displaystyle F_{{\mathcal {P}}_{B}}=F_{{\mathcal {P}}_{D}}}$

Der Satz besagt folgendes:[1][2][3][4][5][6]

Gegeben sei ein Parallelogramm ${\displaystyle {\mathcal {P}}=ABCD}$ der euklidischen Ebene und darin sei ${\displaystyle d}$ eine der beiden Diagonalen, etwa (oBdA) ${\displaystyle d=AC}$.

Weiter sei ${\displaystyle Z}$ ein innerer Punkt von ${\displaystyle d}$.

Durch ${\displaystyle Z}$ seien die beiden Parallelen zu den Seiten von ${\displaystyle {\mathcal {P}}}$ gezogen, welche ${\displaystyle {\mathcal {P}}}$ in vier Teilparallelogramme unterteilen, wobei ${\displaystyle Z}$ deren alleiniger gemeinsamer Punkt ist.

Dann gilt:

Die beiden Teilparallelogramme, welche von der Diagonalen ${\displaystyle d}$ nicht zerlegt werden, also mit ${\displaystyle d}$ allein den Punkt ${\displaystyle Z}$ gemeinsam haben, sind ergänzungsgleich und daher von identischem Flächeninhalt.

Herleitung und Erläuterung

Die vier Teilparallelogramme von ${\displaystyle {\mathcal {P}}}$ seien mit ${\displaystyle {\mathcal {P}}_{A},{\mathcal {P}}_{B},{\mathcal {P}}_{C},{\mathcal {P}}_{D}}$ bezeichnet. Die Indizierung orientiert sich an den Eckpunkten von ${\displaystyle {\mathcal {P}}}$. Es ist also ${\displaystyle {\mathcal {P}}_{X}}$ dasjenige Teilparallelogramm, welches den Eckpunkt   ${\displaystyle X}$   ${\displaystyle (X=A,B,C,D)}$   enthält. Folglich sind aus Konvexitätsgründen die beiden Teilparallelogramme, welche mit der Diagonalen   ${\displaystyle d}$   allein den Punkt ${\displaystyle Z}$ gemeinsam haben, ${\displaystyle {\mathcal {P}}_{B}}$ und ${\displaystyle {\mathcal {P}}_{D}}$, während ${\displaystyle {\mathcal {P}}_{A}}$ und ${\displaystyle {\mathcal {P}}_{C}}$ diejenigen beiden Teilparallelogramme seien, welche mit ${\displaystyle d}$ mehr als einen Punkt gemeinsam haben.

${\displaystyle d}$   zerlegt nun ${\displaystyle {\mathcal {P}}}$ in zwei kongruente Dreiecke, nämlich in ${\displaystyle ABC}$ und ${\displaystyle ACD}$, und genauso zerlegt   ${\displaystyle d}$ sowohl ${\displaystyle {\mathcal {P}}_{A}}$ als auch ${\displaystyle {\mathcal {P}}_{C}}$ jeweils in zwei kongruente Dreiecke.

Sind hier nun ${\displaystyle {\Delta }_{1}}$ und ${\displaystyle {\Delta }_{2}}$ die beiden Zerlegungsdreiecke von ${\displaystyle {\mathcal {P}}_{A}}$ beziehungsweise ${\displaystyle {\Delta }_{3}}$ und ${\displaystyle {\Delta }_{4}}$ die beiden Zerlegungsdreiecke von ${\displaystyle {\mathcal {P}}_{C}}$ und dabei ${\displaystyle {\Delta }_{1}}$ und ${\displaystyle {\Delta }_{3}}$ innerhalb des Dreiecks ${\displaystyle ABC}$ beziehungsweise ${\displaystyle {\Delta }_{2}}$ und ${\displaystyle {\Delta }_{4}}$ innerhalb des Dreiecks ${\displaystyle ACD}$ gelegen, so wird ${\displaystyle ABC}$ in die drei Flächenstücke ${\displaystyle {\Delta }_{1}}$ und ${\displaystyle {\Delta }_{3}}$ und ${\displaystyle {\mathcal {P}}_{B}}$ zerlegt und genauso ${\displaystyle ACD}$ in die drei Flächenstücke ${\displaystyle {\Delta }_{2}}$ und ${\displaystyle {\Delta }_{4}}$ und ${\displaystyle {\mathcal {P}}_{D}}$  .

Folglich ergeben s​ich hinsichtlich d​er Flächeninhalte d​ie Identitäten

(I)   ${\displaystyle F_{ABC}=F_{ACD}={\frac {F_{ABCD}}{2}}}$

(II)   ${\displaystyle F_{ABC}=F_{{\Delta }_{1}}+F_{{\Delta }_{3}}+F_{{\mathcal {P}}_{B}}}$

(III)   ${\displaystyle F_{ACD}=F_{{\Delta }_{2}}+F_{{\Delta }_{4}}+F_{{\mathcal {P}}_{D}}}$

und daraus w​egen der genannten Kongruenzbeziehungen unmittelbar d​ie Identität

(IV)   ${\displaystyle F_{{\mathcal {P}}_{B}}=F_{{\mathcal {P}}_{D}}}$ .

Dies bedeutet auch:

${\displaystyle {\mathcal {P}}_{B}}$   und   ${\displaystyle {\mathcal {P}}_{D}}$ sind ergänzungsgleich.

Denn durch Hinzufügung endlich vieler paarweise kongruenter Vielecke werden aus ${\displaystyle {\mathcal {P}}_{B}}$   und   ${\displaystyle {\mathcal {P}}_{D}}$ zwei kongruente Vielecke erhalten, nämlich die beiden Dreiecke   ${\displaystyle ABC}$   und   ${\displaystyle ACD}$ [7]

Dies beweist d​en Satz.

Zur Terminologie

Die beiden Teilparallelogramme ${\displaystyle {\mathcal {P}}_{B}}$   und   ${\displaystyle {\mathcal {P}}_{D}}$ werden wegen des in dem Satz dargestellten Sachverhalts Ergänzungsparallelogramme genannt. Damit ist auch der Name des Satzes selbst erklärt.

Literatur

• P. S. Alexandroff, A. I. Markuschewitsch, A. J. Chintschin [Red.]: Enzyklopädie der Elementarmathematik. Band V. Geometrie (= Hochschulbücher für Mathematik. Band 11). Deutscher Verlag der Wissenschaften, Berlin 1971.
• Hermann Athen, Jörn Bruhn (Hrsg.): Lexikon der Schulmathematik und angrenzender Gebiete. Band 1. A–E. Aulis Verlag Deubner, Köln 1977, ISBN 3-7614-0242-2.
• Walter Gellert, Herbert Kästner, Siegfried Neuber (Hrsg.): Fachlexikon ABC Mathematik. Verlag Harri Deutsch, Thun / Frankfurt/Main 1978, ISBN 3-87144-336-0.
• Hugo Fenkner, Karl Holzmüller: Mathematisches Unterrichtswerk. Nach den Richtlinien für die Lehrpläne der höheren Schulen Preußens neu bearbeitet von Karl Holzmüller. 12. Auflage. Geometrie. Ausgabe A in 2 Teilen. I. Teil. Verlag von Otto Salle, Berlin 1926.
• Johannes Kratz: Geometrie (= Mathematik für Gymnasien. Band 4). 4. Auflage. Bayerischer Schulbuch Verlag, München 1966.
• Theophil Lambacher, Wilhelm Schweizer (Hrsg.): Lambacher-Schweizer. Mathematisches Unterrichtswerk für höhere Schulen. Geometrie. Ausgabe E. Teil 1. 15. Auflage. Ernst Klett Verlag, Stuttgart 1965.
• Harald Scheid (Hrsg.): DUDEN: Rechnen und Mathematik. 4., völlig neu bearbeitete Auflage. Bibliographisches Institut, Mannheim / Wien / Zürich 1985, ISBN 3-411-02423-2.

Einzelnachweise

1. Hugo Fenkner, Karl Holzmüller: Mathematisches Unterrichtswerk. Nach den Richtlinien für die Lehrpläne der höheren Schulen Preußens neu bearbeitet von Karl Holzmüller. 12. Auflage. Geometrie. Ausgabe A in 2 Teilen. I. Teil. Verlag von Otto Salle, Berlin 1926, S. 127.
2. Johannes Kratz: Geometrie (= Mathematik für Gymnasien. Band 4). 4. Auflage. Bayerischer Schulbuch Verlag, München 1966, S. 172.
3. Theophil Lambacher, Wilhelm Schweizer (Hrsg.): Lambacher-Schweizer. Mathematisches Unterrichtswerk für höhere Schulen. Geometrie. Ausgabe E. Teil 1. 15. Auflage. Ernst Klett Verlag, Stuttgart 1965, S. 59.
4. Fachlexikon ABC Mathematik. S. 135.
5. DUDEN: Rechnen und Mathematik. S. 142.
6. Lexikon der Schulmathematik. Band 1, S. 247.
7. Enzyklopädie der Elementarmathematik. Band V, S. 140.