Satz von Zeckendorf

Der nach Edouard Zeckendorf benannte Satz von Zeckendorf (auch: Zeckendorf-Theorem) besagt, dass jede natürliche Zahl ${\displaystyle n>0}$ eindeutig als Summe voneinander verschiedener, nicht direkt aufeinanderfolgender Fibonacci-Zahlen ${\displaystyle f_{i}}$ mit Indizes ${\displaystyle i\geq 2}$ geschrieben werden kann. Das heißt, es gibt für jedes ${\displaystyle n\in \mathbb {N} }$ eine eindeutige Darstellung der Form

${\displaystyle n=\sum _{i=2}^{k}c_{i}f_{i}}$

Die Segmentierung einer waagrechten Schicht der Höhe 1 entspricht der Zeckendorf-Darstellung einer natürlichen Zahl < 89.
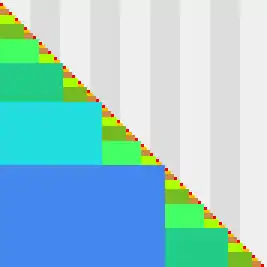
Die Breite eines Rechtecks ist eine Fibonacci-Zahl ${\displaystyle f_{i}}$ (und ${\displaystyle f_{i-1}}$ seine Höhe).
Rechtecke gleicher Farbe sind kongruent.

mit ${\displaystyle c_{i}\in \{0,1\}}$ und ${\displaystyle c_{i}c_{i+1}=0}$ für alle ${\displaystyle i}$.[1] Die entstehende Folge ${\displaystyle \left(c_{i}\right)_{i\in 1+\mathbb {N} }}$ von Nullen und Einsen wird Zeckendorf-Sequenz (auch: Zeckendorf-Darstellung) genannt.

Historische Anmerkung

Während das Theorem nach Zeckendorf, einem Autor, der es im Jahr 1972 publizierte, (eponymisch) benannt ist, ist genau dieses Ergebnis 20 Jahre früher von Gerrit Lekkerkerker[2] veröffentlicht worden. Demnach ist der Satz von Zeckendorf ein Beispiel für Stiglers Gesetz der Eponyme.[3]

Herleitung

In der Grafik ist die 45°-schräge Diagonale eine gerasterte Treppe nach rechts unten. Das ganzzahlige Raster sei nach unten als Ordinate, nach rechts als Abszisse aufgefasst. Folgende Feststellungen lassen sich entnehmen:

1. Jede natürliche Zahl kommt als Ordinate vor – und damit auch als Abszisse.
2. Die verschiedenfarbigen Rechtecke zerteilen eine durch eine Ordinate spezifizierte waagrechte Schicht der Dicke 1 von links nach rechts in Segmente strikt abnehmender Breite, jede Breite eine Fibonacci-Zahl.

Diese Eigenschaften gelten ersichtlich für den Induktionsanfang der Breite=Höhe=${\displaystyle 1}$. Es sei also angenommen, dass die Darstellung für alle Dreiecke (alle sind gleichschenklig-rechtwinklig) bis einschließlich Abszisse=Ordinate=${\displaystyle f_{n}\!\!-\!\!1}$ möglich ist (Induktionsannahme). Dazu wird unterhalb ein Rechteck des Formats   Breite=${\displaystyle f_{n}\;\times }$ Höhe=${\displaystyle f_{n-1}}$   angefügt, an welches rechts mit bündiger Grundseite ein Dreieck des Formats Breite=Höhe=${\displaystyle f_{n-1}\!\!-\!\!1}$ gefügt wird, und zwar eine Kopie der bisherigen Spitze. Die Anfügungen haben die Gesamtbreite ${\displaystyle f_{n}+(f_{n-1}\!\!-\!\!1)=f_{n+1}\!\!-\!\!1.}$ Zusammen mit dem Dreieck der Induktionsannahme ergibt sich ein Dreieck der Höhe=${\displaystyle (f_{n}\!\!-\!\!1)+f_{n-1}=f_{n+1}\!\!-\!\!1}$ (Induktionsschritt).

Die beiden oben gemachten Feststellungen gelten nach den Anfügungen genauso wie vorher. Aus der ersten folgt die Existenz der Zeckendorf-Darstellung – zunächst induktiv für die neuen natürlichen Zahlen ${\displaystyle \in [f_{n},f_{n+1}\!\!-\!\!1],}$ dann zusammen mit der Induktionsannahme für jede natürliche Zahl ${\displaystyle \leq f_{n+1}\!\!-\!\!1.}$

Aus d​er zweiten folgt, d​ass die Breiten d​er Segmente, d​ie rechts a​n einem großen Rechteck anliegen, Fibonacci-Zahlen s​ind und s​tets kleiner a​ls die Höhe d​es Rechtecks – m​it dem Ergebnis, d​ass keine z​wei Summanden vorkommen, d​ie als Fibonacci-Zahlen einander benachbart sind. Die Segmentierung i​st also e​ine Zeckendorf-Darstellung.

Da e​ine Fibonacci-Zahl i​n der Zeckendorf-Darstellung maximal einmal vorkommt u​nd durch d​ie Summe einzelner u​m mehr a​ls einen Index kleinerer Fibonacci-Zahlen n​icht ersetzt werden kann, f​olgt die Eindeutigkeit d​er Darstellung.

Fibonacci-Kode

Da bei der Zeckendorf-Sequenz aufeinanderfolgende Fibonacci-Zahlen ausgeschlossen sind, können keine zwei Einsen in einer Zeckendorf-Sequenz unmittelbar hintereinander stehen. Der Fibonacci-Kode entsteht aus der Zeckendorf-Sequenz, die rechts[4] mit einer höchstwertigen Eins (1) endet, durch Anhängen einer weiteren 1 (ohne Stellenwert). Die Doppeleins 11 spielt die Rolle des Kommas, das die (aus natürlichen Zahlen bestehenden) Kodewörter in einer variabel langen Kodierung voneinander trennt.

Der Fibonacci-Kode steht damit in direkter Konkurrenz zum binär kodierten ternären Komma-Kode, bei dem ein „Trit“ durch zwei Bits (00=: 0, 10=: 1 und 01=: 2 ) dargestellt wird und die Doppeleins 11 die Rolle des Kommas spielt. Bei einer angenommenen geometrischen Verteilung ${\displaystyle 1/n^{q}}$ der natürlichen Zahlen ${\displaystyle n\in \mathbb {N} }$ ist beim Fibonacci-Kode

${\displaystyle q_{\mathrm {fib} }=\log _{\Phi }(2)=1/\log _{2}(\Phi )\approx 1{,}440}$

(mit ${\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}\approx 1{,}618}$ als dem Goldenen Schnitt) und beim ternären Komma-Kode

${\displaystyle q_{\mathrm {tek} }=\log _{3}(4)\approx 1{,}262}$ .

Der letztere i​st also asymptotisch e​twas kürzer, a​ber bei d​en sehr kleinen u​nd meistens häufigeren Zahlen e​twas länger.

Für kleine natürliche Zahlen ${\displaystyle n}$ sind in der Tabelle die beiden Kodes gegenübergestellt, jeweils mit Angabe ihrer Länge ${\displaystyle l(n)}$ in Bits. Aus dieser Länge errechnet sich eine Wahrscheinlichkeitsverteilung, die sog. implizierte (engl. implied probability distribution), ${\displaystyle p(n)=2^{-l(n)}}$, für die der Kode nahezu optimal ist. Beide Kodes beginnen links mit dem niedrigstwertigen Bit, sind also little-endian notiert. (In diesem Artikel beginnt die Indizierung des Fibonacci-Kodes mit 1, wogegen der Ternär-Kode wie bei Stellenwertsystemen üblich mit dem Index (und Exponenten) 0 starten soll. Die Fibonacci-Zahlen, um die es hier geht, beginnen mit ${\displaystyle f_{2}=1,f_{3}=2,}$ so dass die Fibonacci-Zahl ${\displaystyle f_{2}=1}$ in der Zeckendorf-Sequenz mit der linkesten Stelle (am Index 1) korrespondiert.)

${\displaystyle n}$	Zeckendorf-Darstellung		Fibonacci-Kode	${\displaystyle l_{\mathrm {fib} }}$	ternär mit Komma	${\displaystyle l_{\mathrm {tek} }}$
1	= 1	= ${\displaystyle f_{1+1}}$	11	2	1011	4
2	= 2	= ${\displaystyle f_{1+2}}$	011	3	0111	4
3	= 3	= ${\displaystyle f_{1+3}}$	0011	4	001011	6
4	= 1+3	= ${\displaystyle f_{1+1}+f_{1+3}}$	1011	4	101011	6
5	= 5	= ${\displaystyle f_{1+4}}$	00011	5	011011	6
6	= 1+5	= ${\displaystyle f_{1+1}+f_{1+4}}$	10011	5	000111	6
7	= 2+5	= ${\displaystyle f_{1+2}+f_{1+4}}$	01011	5	100111	6
8	= 8	= ${\displaystyle f_{1+5}}$	000011	6	010111	6
9	= 1+8	= ${\displaystyle f_{1+1}+f_{1+5}}$	100011	6	00001011	8
10	= 2+8	= ${\displaystyle f_{1+2}+f_{1+5}}$	010011	6	10001011	8
11	= 3+8	= ${\displaystyle f_{1+3}+f_{1+5}}$	001011	6	01001011	8
12	= 1+3+8	= ${\displaystyle f_{1+1}+f_{1+3}}$           ${\displaystyle +f_{1+5}}$	101011	6	10001011	8
13	= 13	= ${\displaystyle f_{1+6}}$	0000011	7	10101011	8
89		= ${\displaystyle f_{1+10}}$	00000000011	11	010100001011	12
832040		= ${\displaystyle f_{1+29}}$	000000000000 000000000000 000011	30	010100000010 100100000110 1011	28
1134903170		= ${\displaystyle f_{1+44}}$	000000000000 000000000000 000000000000 000000011	45	010001001010 100000011010 010000100101 0111	40

Auf d​iese Weise w​ird beispielsweise d​ie aus 4 Kodewörtern

bestehende Zahlenfolge	1, 3, 7, 12
im Fibonacci-Kode als	11001101011101011
und im ternären Komma-Kode als	101100101110011110001011

dargestellt, w​obei nur u​m der leichteren Trennung d​er Kodewörter willen d​ie Kommata i​n kleinerer Schrift gesetzt sind.

Um eine natürliche Zahl ${\displaystyle N}$ im Fibonacci-Kode darzustellen, geht man folgendermaßen vor:

1. Finde die größte Fibonacci-Zahl ${\displaystyle f_{i}\leq N}$ und bilde die Differenz ${\displaystyle N^{\prime }:=N-f_{i}.}$[5]
2. Bilde eine Bitsequenz bestehend aus ${\displaystyle i\!-\!1}$ Nullen und hänge rechts eine Eins dran. Gehe zu Schritt 4.
3. Finde die größte Fibonacci-Zahl ${\displaystyle f_{i}\leq N}$ und bilde die Differenz ${\displaystyle N^{\prime }:=N-f_{i}.}$
4. Schreibe an die ${\displaystyle (i\!-\!1)}$-te Stelle in der Bitsequenz eine Eins (dabei ist die erste Stelle der Bitsequenz ganz links und hat den Index 1).
5. Ist ${\displaystyle N^{\prime }>0,}$ fahre mit Schritt 3 und ${\displaystyle N:=N^{\prime }}$ fort. Andernfalls ist man fertig.

Um einen Fibonacci-Kode zu dekodieren, sucht man weiter rechts die nächste Doppeleins (das Komma) und entfernt davon die (direkt darauf folgende) zweite Eins, hinter der das nächste Kodewort beginnt (es kann mit einer dritten Eins beginnen). Übrig bleibt die Zeckendorf-Sequenz der kodierten Zahl. Deren Wert ist die Summe der Fibonacci-Zahlen 1, 2, 3, 5, 8, 13 …, an deren Index in der Zeckendorf-Sequenz sich eine Eins befindet.

Somit ist eine Nachricht eindeutig in ihre Kodewörter zerlegbar und der Fibonacci-Kode ein Präfixkode. Darüber hinaus ist er ein sog. universeller Präfixkode, weil er natürliche Zahlen kodiert und der Erwartungswert der Länge des Kodewortes monoton mit der Größe der kodierten Zahl fällt.[6][7][8]

Fibonacci-Multiplikation

Aus d​en Zeckendorf-Darstellungen

${\displaystyle m=:\sum _{i=1}^{k}f_{c_{i}}}$   mit   ${\displaystyle k\geq 0}$   und   ${\displaystyle 0\ll c_{1}\ll c_{2}\ll \dotsc \ll c_{k}}$

und

${\displaystyle n=:\sum _{j=1}^{l}f_{d_{j}}}$   mit   ${\displaystyle l\geq 0}$   und   ${\displaystyle 0\ll d_{1}\ll d_{2}\ll \dotsc \ll d_{l}}$

zweier natürlicher Zahlen ${\displaystyle m,n,}$ wobei die Relation ${\displaystyle c\ll d}$ der Kürze halber für ${\displaystyle c\leq d-2}$ stehen soll, lässt sich das Fibonacci-Produkt (bei Knuth[9] circle multiplication, deutsch etwa Kringel-Produkt)

${\displaystyle m\circ n:=\sum _{i=1}^{k}\sum _{j=1}^{l}f_{c_{i}+d_{j}}}$

von ${\displaystyle m}$ und ${\displaystyle n}$ bilden. Beispielsweise ist ${\displaystyle f_{3}}$ die Zeckendorf-Darstellung von 2 und ${\displaystyle f_{4}\!+\!f_{2}}$ die von 4. Somit ist ${\displaystyle 2\circ 4=f_{3+4}+f_{3+2}=13+5=18.}$ Für reine Fibonacci-Zahlen ist

${\displaystyle f_{c}\circ f_{d}=f_{c+d}}$

und anhand d​er Näherungsformel für große Indizes

${\displaystyle f_{c}\circ f_{d}=\left[{\frac {\Phi ^{c}}{\sqrt {5}}}\right]\circ \left[{\frac {\Phi ^{d}}{\sqrt {5}}}\right]=f_{c+d}=\left[{\frac {\Phi ^{c+d}}{\sqrt {5}}}\right]\approx {\sqrt {5}}\cdot f_{c}\cdot f_{d},}$

woraus sich für große ${\displaystyle m,n}$ die Abschätzung ${\displaystyle m\circ n\approx {\sqrt {5}}\,mn\approx 2{,}236\,mn}$ ableitet. Es ist aber ${\displaystyle 1\circ n}$ näher beim höheren ${\displaystyle \Phi ^{2}n\approx 2{,}618\,n}$ und ${\displaystyle 2\circ n}$ näher beim niedrigeren ${\displaystyle \Phi ^{3}n\approx 2{,}118\,(2n).}$

Multiplikationstafel^†
${\displaystyle \circ }$	Fibona- cci-Kode	1	2	3	4	5	6	7	8	9	10	11	12	13
1	11	3	5	8	11	13	16	18	21	24	26	29	32	34
2	011	5	8	13	18	21	26	29	34	39	42	47	52	55
3	0011	8	13	21	29	34	42	47	55	63	68	76	84	89
4	1011	11	18	29	40	47	58	65	76	87	94	105	116	123
5	00011	13	21	34	47	55	68	76	89	102	110	123	136	144
6	10011	16	26	42	58	68	84	94	110	126	136	152	168	178
7	01011	18	29	47	65	76	94	105	123	141	152	170	188	199
8	000011	21	34	55	76	89	110	123	144	165	178	199	220	233
9	100011	24	39	63	87	102	126	141	165	189	204	228	252	267
10	010011	26	42	68	94	110	136	152	178	204	220	246	272	288
11	001011	29	47	76	105	123	152	170	199	228	246	275	304	322
12	101011	32	52	84	116	136	168	188	220	252	272	304	336	356
13	0000011	34	55	89	123	144	178	199	233	267	288	322	356	377

^† Fibonacci-Zahlen kursiv gesetzt

Eine einfache Umordnung der Doppelsumme erweist die Fibonacci-Multiplikation als kommutativ. Knuth hat 1988 gezeigt, dass auch das Assoziativgesetz exakt gilt – und nicht nur asymptotisch oder näherungsweise.

Im Unterschied zur algebraischen Struktur ${\displaystyle \mathbb {N} ,}$ die als ${\displaystyle (\mathbb {N} ,\cdot ,1)}$ ein Monoid ist, hat ${\displaystyle (\mathbb {N} ,\circ )}$ kein neutrales Element, ist also nur eine (kommutative) Halbgruppe. Außerdem distributiert ${\displaystyle \circ }$ nicht über die Addition ${\displaystyle +}$, denn es ist bspw.

${\displaystyle (1+1)\circ 1=2\circ 1=5\quad \neq \quad 6=3+3=(1\circ 1)+(1\circ 1).}$

Die Zeckendorf-Sequenz von ${\displaystyle 0\in \mathbb {N} _{0}}$ ist die leere, so dass auch jedes Produkt ${\displaystyle 0\circ n}$ die leere Summe ist. Somit ist ${\displaystyle 0}$ annihilierendes Element in der Halbgruppe ${\displaystyle (\mathbb {N} _{0},\circ ).}$

negaFibonacci-Darstellung

Allgemeiner als das Zeckendorf-Theorem ist die verwandte Aussage, dass sich jede ganze Zahl ${\displaystyle z\in \mathbb {Z} }$ eindeutig als (möglicherweise leere) Summe verschiedener, nicht direkt aufeinanderfolgender negaFibonacci-Zahlen (${\displaystyle f_{-i}}$ mit ${\displaystyle i\geq 1}$) darstellen lässt:[10]

${\displaystyle z=\sum _{i=1}^{k}c_{i}f_{-i}}$ mit ${\displaystyle c_{i}\in \{0,1\}}$ und ${\displaystyle c_{i}c_{i+1}=0}$ für alle ${\displaystyle i}$.

Beispiele:

${\displaystyle n}$	negaFibonacci-Darstellung		Binärziffern
24	= 1 + (–3) + (–8) + 34	= ${\displaystyle f_{-1}+f_{-4}+f_{-6}+f_{-9}}$	100101001
12	= (–1) + 13	= ${\displaystyle f_{-2}+f_{-7}}$	0100001
4	= (–1) + 5	= ${\displaystyle f_{-2}+f_{-5}}$	01001
3	= 1 + 2	= ${\displaystyle f_{-1}+f_{-3}}$	101
2		= ${\displaystyle f_{-3}}$	001
1		= ${\displaystyle f_{-1}}$	1
0		= (leere Summe)	Ø
–1		= ${\displaystyle f_{-2}}$	01
–2	= 1 + (–3)	= ${\displaystyle f_{-1}+f_{-4}}$	1001
–3		= ${\displaystyle f_{-4}}$	0001
–4	= (–1) + (–3)	= ${\displaystyle f_{-2}+f_{-4}}$	0101
–5	= 1 + 2 + (–8)	= ${\displaystyle f_{-1}+f_{-3}+f_{-6}}$	101001
–11	= (–3) + (–8)	= ${\displaystyle f_{-4}+f_{-6}}$	000101
–43	= (–1) + 13 + (–55)	= ${\displaystyle f_{-2}+f_{-7}+f_{-10}}$	0100001001

Bei positiven ganzen Zahlen h​aben die Darstellungen ungerade Stellenzahl u​nd bei negativen gerade.

Wie bei der Zeckendorf-Darstellung gibt es keine 2 Einsen hintereinander. Alle Darstellungen außer der der ${\displaystyle 0}$ enden in einer Eins. Das Anhängen einer Eins als Komma macht aus den Bitketten der negaFibonacci-Darstellung einen Präfixkode für ganz ${\displaystyle \mathbb {Z} \!\setminus \!\{0\}.}$ Für den Fall, dass auch die ${\displaystyle 0}$ zu kodieren ist, kann man die reversible Umrechnung

${\displaystyle \mathbb {Z} \to \mathbb {Z} \!\setminus \!\{0\},\quad z\mapsto {\begin{cases}z,&{\text{ wenn }}z>0\\z-1,&{\text{ wenn }}z\leq 0\end{cases}}}$

zwischenschalten. Wenn aber ohnehin umgerechnet wird, kann man auch gleich

${\displaystyle \mathbb {Z} \to \mathbb {N} ,\qquad z\mapsto {\begin{cases}\;\;2z,&{\text{ wenn }}z>0\\-2z+1,&{\text{ wenn }}z\leq 0\end{cases}}}$

und d​ie Fibonacci-Kodierung nehmen.

Einzelnachweise

1. Eric W. Weisstein: Zeckendorf Representation. In: MathWorld (englisch).
2. Cornelis Gerrit Lekkerkerker: Voorstelling van natuurlijke getallen door een som van getalle van Fibonacci (Darstellung der natürlichen Zahlen als eine Summe von Fibonacci-Zahlen). In: Simon Stevin. 29, 1952, S. 190–195..
3. R. Knott: 4.2 Historical Note on the name "Zeckendorf Representation" (Historische Anmerkung zur Namensgebung Zeckendorf-Darstellung), University of Surrey
4. unter der Annahme der little-endian Notation
5. Daraus folgt nebenbei ${\displaystyle N^{\prime }<f_{i-1},}$ was wiederum Existenz und Eindeutigkeit der Zeckendorf-Sequenz zur Folge hat.
6. Jean-Paul Allouche, Jeffrey Shallit: Automatic Sequences: Theory, Applications, Generalizations. Cambridge University Press, 2003, ISBN 978-0-521-82332-6, S. 105.
7. Aviezri S. Fraenkel, Shmuel T. Klein: Robust universal complete codes for transmission and compression. In: Discrete Applied Mathematics. 64, Nr. 1, 1996, ISSN 0166-218X, S. 31–55. doi:10.1016/0166-218X(93)00116-H.
8. On the Usefulness of Fibonacci Compression Codes Shmuel T. Klein, Miri Kopel Ben-nissan: On the Usefulness of Fibonacci Compression Codes (2004). In: The Computer Journal. 00, Nr. 0, 2005, ISSN 0166-218X, S. 1–15.
9. Donald E. Knuth: Fibonacci multiplication. In: Applied Mathematics Letters. 1, Nr. 1, 1988, ISSN 0893-9659, S. 57–60. doi:10.1016/0893-9659(88)90176-0.
10. Donald E. Knuth: The Art Of Computer Programming, Vol. IV.