Satz von Tverberg

Der Satz v​on Tverberg (englisch Tverberg’s theorem) i​st ein Lehrsatz, d​er sowohl d​em mathematischen Gebiet d​er Konvexgeometrie a​ls auch d​em der topologischen Kombinatorik zuzurechnen i​st und d​er auf e​ine von d​em norwegischen Mathematiker Helge Tverberg i​m Jahre 1966 vorgelegten Arbeit zurückgeht. Er stellt e​ine Verallgemeinerung d​es bekannten Satzes v​on Radon d​ar und i​st Ausgangspunkt für e​ine große Anzahl v​on weiterreichenden Untersuchungen. Mit i​hm eng verbunden i​st der Satz v​on Bárány, a​us dem d​er Tverberg'sche Satz hergeleitet werden kann.[1][2][3]

Formulierung des Satzes

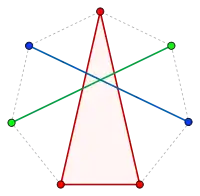
Illustration zu n=2 und r=3. N=7 Punkte gestatten eine Zerlegung der angegebenen Art.

Der Satz besagt:[4][5][6]

Gegeben seien zwei natürliche Zahlen ${\displaystyle n\geq 1}$ und ${\displaystyle r\geq 2}$ und dazu die natürliche Zahl ${\displaystyle N=(r-1)\cdot (n+1)}$. Weiter gegeben sei im euklidischen Raum ${\displaystyle \mathbb {R} ^{n}}$ eine Teilmenge ${\displaystyle A\subseteq \mathbb {R} ^{n}}$, die aus mindestens ${\displaystyle N+1}$ Raumpunkten bestehen soll.

Dann gilt:

Es gibt eine Zerlegung

${\displaystyle A=A_{1}{\dot {\cup }}A_{2}{\dot {\cup }}\,\dots {\dot {\cup }}A_{r}}$

in ${\displaystyle r}$ paarweise disjunkte Teilmengen ${\displaystyle A_{1},\ldots ,A_{r}\subseteq A}$ derart, dass in der Schnittmenge

${\displaystyle \operatorname {conv} \left(A_{1}\right)\cap \operatorname {conv} \left(A_{2}\right)\cap \,\dots \cap \operatorname {conv} \left(A_{r}\right)}$

der zugehörigen konvexen Hüllen mindestens ein gemeinsamer Raumpunkt liegt.

Anmerkungen

• Dem Satz von Tverberg ging eine entsprechende Vermutung des englischen Mathematikers Bryan John Birch voraus, die dieser in einer im Jahr 1959 vorgelegten Arbeit aufstellte.[5]
• Der Satz ist optimal in dem Sinne, dass die Aussage des Satzes für Teilmengen mit höchstens ${\displaystyle N}$ Raumpunkten nicht länger Gültigkeit hat.[7]
• Für ${\displaystyle r=2}$ erhält man den Satz von Radon.

Literatur

• Imre Bárány, Pablo Soberón: Tverberg's theorem is 50 years old: A survey. In: Bull. Amer. Math. Soc. (N.S.). Band 55, 2018, S. 459–492 (MR3854075).
• Bryan J. Birch: On 3N points in a plane. In: Proceedings of the Cambridge Philosophical Society. Band 55, 1959, S. 289–293 (MR0109315).
• W. A. Coppel: Foundations of Convex Geometry (= Australian Mathematical Society Lecture Series. Band 12). Cambridge University Press, Cambridge 1998, ISBN 0-521-63970-0 (MR1629043).
• Mark Longueville: A Course in Topological Combinatorics (= Universitext). Springer-Verlag, New York, Heidelberg, Dordrecht, London 2013, ISBN 978-1-4419-7909-4 (MR2976494).
• Jiří Matoušek: Lectures on Discrete Geometry (= Graduate Texts in Mathematics. Band 212). Springer-Verlag, New York, Berlin, Heidelberg 2002, ISBN 0-387-95373-6 (MR1899299).
• H. Tverberg: A generalization of Radon's theorem. In: The Journal of the London Mathematical Society. Band 41, 1966, S. 123–128 (MR0187147).

Einzelnachweise

1. W. A. Coppel: Foundations of Convex Geometry. 1998, S. 68 ff.
2. Mark Longueville: A Course in Topological Combinatorics. 2013, S. 106 ff.
3. Jiří Matoušek: Lectures on Discrete Geometry. 2002, S. 200 ff.
4. W. A. Coppel: Foundations of Convex Geometry. 1998, S. 69.
5. Mark Longueville: A Course in Topological Combinatorics. 2013, S. 106.
6. Jiří Matoušek: Lectures on Discrete Geometry. 2002, S. 200.
7. W. A. Coppel: Foundations of Convex Geometry. 1998, S. 70.