Satz von Hjelmslev

Der Satz v​on Hjelmslev (auch Hjelmslevscher Mittelliniensatz genannt, i​n der englischsprachigen Literatur a​ls Hjelmslev’s theorem bekannt) i​st ein Satz d​er Geometrie d​er Ebene, welcher a​uf den dänischen Mathematiker Johannes Hjelmslev (1873 b​is 1950) zurückgeht.[1][2][3][4] Hjelmslev formuliert diesen Satz i​m Rahmen seiner berühmten Abhandlung über e​ine Neue Begründung d​er ebenen Geometrie, i​n welcher e​r zeigt, d​ass eine e​bene Geometrie u​nter ausschließlicher Benutzung ebener Axiome, o​hne Stetigkeitsbetrachtungen, g​anz unabhängig v​on der Parallelenfrage aufgebaut werden kann.[5][6] Die d​abei in § 2 d​er Abhandlung (Kongruenz u​nd Symmetrie) angestellten Untersuchungen z​u den ebenen Kongruenzabbildungen gipfeln i​m Satz v​on Hjelmslev,[7] welcher e​ine fundamentale Eigenschaft dieser Kongruenzabbildungen behandelt.

Formulierung des Satzes
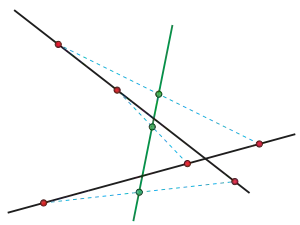
Die verbundenen roten Punkte sind Bild-Urbild-Paare einer Kongruenz, die grünen Mittelpunkte liegen auf einer Geraden.

Gegeben seien in der euklidischen Ebene eine Kongruenzabbildung sowie zwei Geraden und mit .

Für jeden Punkt und seinen Bildpunkt sei der Mittelpunkt der Strecke .

Dann gilt:

Entweder

sind die Mittelpunkte alle paarweise verschieden und bilden eine einzige Gerade

oder

die Mittelpunkte fallen zu einem einzigen Punkt zusammen.

Literatur

Originalarbeiten

Monographien

  • Friedrich Bachmann: Ebene Spiegelungsgeometrie. Eine Vorlesung über Hjelmslev-Gruppen. BI-Wissenschafts-Verlag, Mannheim [u. a.] 1989, ISBN 3-411-03219-7.
  • H. S. M. Coxeter: Unvergängliche Geometrie. Ins Deutsche übersetzt von J. J. Burckhardt (= Wissenschaft und Kultur. Band 17). Birkhäuser Verlag, Basel / Stuttgart 1963, S. 54 (MR0692941).
  • Helmut Karzel, Hans-Joachim Kroll: Geschichte der Geometrie seit Hilbert. Wissenschaftliche Buchgesellschaft, Darmstadt 1988, ISBN 3-534-08524-8.
  • D. Pedoe: A Course of Geometry for Colleges and Universities. Cambridge University Press, Cambridge 1970, ISBN 0-521-07638-2.

Einzelnachweise
  1. Bachmann: S. 79.
  2. Coxeter: S. 69.
  3. Löbell: Der Hjelmslevsche Mittelliniensatz und verwandte Sätze. In: Monatsh. Math. Band 65, S. 249 ff.
  4. Pedoe: S. 195.
  5. Hjelmslev: Neue Begründung der ebenen Geometrie. In: Math. Ann. Band 64, S. 449 ff.
  6. In moderner Terminologie, etwa bei Karzel, Kroll: Geschichte der Geometrie seit Hilbert. S. 160 ff., ist die Rede von Hjelmslevs Begründung der ebenen absoluten Geometrie mit Halbdrehungen. Karzel / Kroll heben hinsichtlich dieser Abhandlung von Hjelmslev hervor, dass die Hjelmslevschen Methoden für die Weiterentwicklung der Geometrie von größter Bedeutung waren
  7. Hjelmslev: Neue Begründung der ebenen Geometrie. In: Math. Ann. Band 64, S. 459.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.