Rundschnitt (Fachwerk)
Ein Rundschnitt (auch Rundschnittverfahren, Knotenpunktverfahren, Knotenpunktmethode, Knotenschnittverfahren oder Knotengleichgewichtsverfahren) ist ein Berechnungsverfahren der Baustatik für Schnittreaktionen und wird hauptsächlich bei Fachwerken verwendet. Beim Rundschnitt wird in Gedanken ein Knoten im Fachwerk „rundherum“ herausgeschnitten, um die Kräfte, die an diesem Knoten kurzgeschlossen werden, zu betrachten. Auf die an den Knoten angeschlossenen Stäbe wirken bei einem idealen Fachwerk ausschließlich Normalkräfte, welche in diesem Zusammenhang oft als Stabkräfte bezeichnet werden.
Berechnungsverfahren
Jeder Knoten muss sich im Gleichgewicht befinden. Dazu nimmt man die Kräftegleichgewichte jeder Vektorkomponente zu Hilfe. Das (vektorielle) Momentengleichgewicht um einen einzelnen idealen Fachwerksknoten ist vorausgesetzt, da laut Theorie alle Stäbe ausschließlich Normalkräfte haben, deren Wirkungslinie in der Stabachse liegt. Diese Wirkungslinien gehen laut Theorie genau durch den gelenkigen Knoten, deshalb ist die Summe aller Momente um den Knoten gleich null. Für 2-D- und 3-D-Fachwerke gilt: je Dimension gibt es eine lineare unabhängige Kraftgleichgewichtsbedingung.
Nachzuweisen wäre das Fachwerk in der verformten Lage mit den dazugehörigen Stabwinkeln, da es sich dort (und nur dort) im Gleichgewicht befindet. Da die Stabachsendrehwinkel bei baupraktischen Beispielen in der Regel (betragsmäßig) vernachlässigbar klein bleiben (|φ(x)|≤0.1[1]), kann man im Allgemeinen problemlos mit den planmäßigen Stabwinkeln und Stablängen rechnen, da sich diese nur geringfügig von den tatsächlichen Stabwinkeln und Stablängen unterscheiden.
2D
Das Rundschnittverfahren wird üblicherweise für den Sonderfall eines ebenen Fachwerks gelehrt, welches eine horizontale und vertikale Richtung hat. Hier kann man einen beliebigen Knoten herausschneiden, unabhängig davon, wie viele unbekannte und bekannte Kräfte auf diesen Knoten wirken. Das vektorielle Kräftegleichgewicht wird üblicherweise mit zwei skalaren, linear unabhängigen Gleichgewichtsbedingungen
- Summe der Horizontalkräfte gleich Null und
- Summe der Vertikalkräfte gleich Null
angegeben. Es kann jedes statisch bestimmte ideale Fachwerk ausschließlich mit Rundschnitt gelöst werden, auch die Auflagerkräfte können damit berechnet werden, jedoch ist es in der Regel einfacher, die Auflagerreaktionen vorab zu ermitteln. Für die Berechnung eines Fachwerks wird dennoch oft eine Kombination aus Rundschnitt und Ritterschnitt verwendet, um möglichst unabhängige Gleichungen und somit leicht zu lösende Gleichungssysteme zu erhalten. Sind ausschließlich bis zu zwei Kräfte eines Knotens unbekannt, deren Wirkungslinien nicht parallel sind, kann man jede dieser Kräfte mit einem eindimensionalen unabhängigen Gleichungssystem berechnen, indem man die Summe der Kräfte in eine beliebige Richtung betrachtet, die orthogonal zu allen anderen unbekannten Kräften dieses Knoten steht.
Nullstäbe in 2D
Da die Knoten in einem idealen Fachwerk als zentrale Kräftegruppen idealisiert werden, basiert die Bestimmung der Nullstäbe auf der Überlegung, dass die Kräfte im Gleichgewicht sind. Drei Kräfte, die jeweils ungleich Null sind, können in einer ebenen zentralen Kräftegruppe nur dann im Gleichgewicht sein, wenn keine zwei der drei Kräfte zueinander kollinear sind. Die Regeln für Nullstäbe sind somit:
- Sind an einem unbelasteten Knoten zwei Stäbe angeschlossen, die nicht in gleicher Richtung liegen (unbelasteter Stabzweischlag), so sind beide Stäbe Nullstäbe.
- Sind an einem belasteten Knoten zwei (nicht kollineare) Stäbe angeschlossen und greift die äußere Kraft in Richtung des einen Stabes an, so ist der andere Stab in der Theorie I Ordnung (Gleichgewicht in der undeformierten Lage) ein Nullstab.
- Sind an einem unbelasteten Knoten drei Stäbe angeschlossen, von denen zwei in gleicher Richtung liegen, so ist der dritte Stab in der Theorie I Ordnung (Gleichgewicht in der undeformierten Lage) ein Nullstab.
Einfaches Beispiel
Ein statisch bestimmtes Fachwerk mit horizontalen Stäben und Stäben unter einem Winkel von ±π/4 (≙±45°).
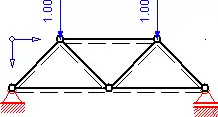
Die Kräfte können ein beliebiges Vielfaches von 1 Newton sein. Aufgrund von statischen Symmetriebedingungen folgt:
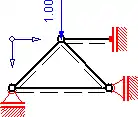
Da es sich um ein statisch bestimmtes Fachwerk handelt, ist es vorteilhaft, die vier unbekannten Auflagerkräfte (eine vertikale und zwei horizontale Kräfte sowie ein Einspannmoment) mittels äußerem (globalen) Gleichgewicht zu berechnen:
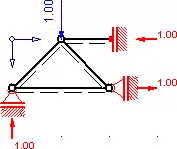
Das Auflagermoment im Obergurt ergibt Null, indem man die Querkraft des Obergurtes mit Null identifiziert, da keine vertikale Auflagerkraft vorhanden ist, das Moment beim Gelenk gleich Null ist und, aufgrund der Differentialbeziehung zwischen Moment und Querkraft, bei einer Querkraft gleich Null das Moment konstant ist.
Einführen von Stabbezeichnungen:
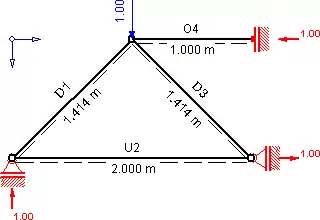
Man schneidet einen beliebigen Knoten heraus. Um den Rechenaufwand gering zu halten, ist es von Vorteil, einen Knoten mit maximal zwei unbekannten Kräften auszusuchen, welche nicht parallel sind. (Der obere Knoten wäre nicht geeignet, weil dieser drei noch unbekannte Stabkräfte hat.) Um es übersichtlich zu halten, nennt man die Normalkraft oft analog zur Stabbezeichnung, was mathematisch nicht ganz korrekt ist. Die korrekte Schreibweise für z. B. die Normalkraft im Stab D1 könnte sein: N_{D1}.
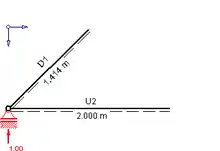
Man nimmt zum Beispiel das linke Auflager, bei dem zwei nicht parallele unbekannte Stabkräfte angreifen. ΣH=0 würde zwei Unbekannte beinhalten und dazu führen, dass D1+√(2)⋅U2=0, womit nicht sofort eine Stabkraft ermittelt werden könnte. Hingegen bei ΣV=0 (orthogonal zum Untergurt U1), taucht als einzige Unbekannte die Diagonale D1 auf. ΣV=0 umgeschrieben als ΣVnachOben=ΣVnachUnten führt zu: 1⋅[N]+D1⋅sin(45°)=0 durch Umformen folgt D1=-√(2)⋅[N]. Mit ΣVnachRechts=ΣVnachLinks folgt: (√(2)⋅[N])⋅cos(45°)=U2, damit ergibt sich U2=+1⋅[N]. Um keine Vorzeichen zu vergessen, empfiehlt es sich, auch bei positiven Werten ein Vorzeichen dazuzuschreiben.
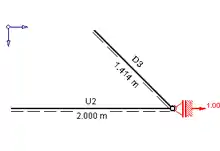
Jetzt sind nur mehr die Diagonale D2 und der Obergurt O4 unbekannt. Darauf kann man D2 z. B. mit ΣV=0 beim (unteren) Symmetrieknoten berechnen und erfährt, dass es ein Nullstab ist, da außer D2 an dem Knoten keine anderen vertikalen Kräfte angreifen. Um die Richtigkeit der bisherigen Rechnung stichprobenartig zu kontrollieren, kann man auch ΣHnachRechts=ΣHnachLinks an dem Knoten berechnen, bekommt als Ergebnis 1⋅[N]=1⋅[N] und somit eine wahre Aussage.
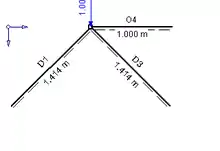
Jetzt gibt es nur mehr einen Fachwerksknoten, bei dem man noch einen Rundschnitt machen kann, und zwar den Knoten oben. ΣV=0 führt bei korrekter Berechnung zu einer wahren Aussage (0=D1⋅sin(45°)+1⋅[N]). Für das Gleichgewicht ist es irrelevant, ob es sich um eine äußere Einwirkung, eine Stabkraft oder eine Auflagerkraft handelt, deshalb wird es gleich behandelt. Mit ΣHnachRechts=ΣHnachLinks folgt: O4=D1⋅cos(45°) durch Einsetzen bekommt man O4=-1⋅[N]
Somit ergibt sich für das gesamte Fachwerk:
D1=-√(2)⋅[N]
U2=1⋅[N]
D3=±0
O4=-1⋅[N]
U5=U2=1⋅[N]
D6=D3=±0
D7=D1=-√(2)⋅[N]
Abgrenzung des Begriffes
Mehrere Knoten
Einen Rundschnitt könnte man problemlos erweitern, indem man mehrere Knoten herausschneidet und dann das Kräftegleichgewicht betrachtet. Das wird jedoch üblicherweise als Ritterschnitt bezeichnet, auch wenn dieser zusätzlich das Momentengleichgewicht in Betracht zieht. Ein Rundschnitt kann als Sonderfall des Ritterschnitts betrachtet werden.
Momentengleichgewicht
Prinzipiell wäre es möglich, die Gleichungssysteme für jeden Rundschnitt ausschließlich mit Momentengleichgewichtsbedingungen aufzustellen. Im Prinzip ist auch ein Kräftegleichgewicht nichts anderes als ein Momentengleichgewicht eines Punktes, der unendlich weit entfernt ist. Bei einem idealen Fachwerksknoten ist es jedoch sinnlos, die Momente um den Knoten selbst zu betrachten, da sie keine Aussage über die Stabachsenkräfte ermöglichen. Eine sinnvolle Wahl von Punkten müsste linear unabhängig von Knotenpunkten und allen anderen „Betrachtungspunkten“ sein, um mit jedem Momentengleichgewicht eine neue linear unabhängige Gleichung aufstellen zu können.
Literatur
- Bernhard Pichler, Josef Eberhardsteiner: Baustatik VO - LVA-Nr 202.065. Hrsg.: E202 Institut für Mechanik der Werkstoffe und Strukturen – Fakultät Bauingenieurwesen, TU Wien. SS 2017 Auflage. TU Verlag, Wien 2017, ISBN 978-3-903024-41-0, 6.3 Knotengleichgewichtsverfahren (Rundschnittverfahren) (516 S., tuverlag.at – Erstausgabe: 2012).
- Kalliauer J.: Prüfungsfragenausarbeitung von Mechanik 1 (TU-Wien). (PDF) Kalliauer J., Juni 2012, S. 35–36, abgerufen am 6. November 2015.
- Christian Spura: Technische Mechanik 1. Stereostatik. Springer, Wiesbaden 2016, ISBN 978-3-658-14984-0.
Siehe auch
- analoges Verfahren für Biegestäbe: Schnittreaktion
- alternatives Verfahren für Fachwerke: Ritterschnitt
- ein 1-D-Fachwerk wird üblicherweise als axial beanspruchter Gerberträger bezeichnet
Einzelnachweise
- Bernhard Pichler, Josef Eberhardsteiner: Baustatik VO LVA-Nr 202.065. Hrsg.: E202 Institut für Mechanik der Werkstoffe und Strukturen – Fakultät Bauingenieurwesen, TU Wien. SS 2017 Auflage. TU Verlag, Wien 2017, ISBN 978-3-903024-41-0, 2.4 Lineare geometrische Beziehungen (516 S., tuverlag.at – Erstausgabe: 2012). Baustatik VO LVA-Nr 202.065 (Memento des Originals vom 17. Juli 2017 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.