Quantum Walk

Im Bereich der Quanteninformatik ist der Quantum Walk (auch Quantum Random Walk) das Analogon zum klassischen Random Walk. Während beim klassischen Random Walk ein Zustand durch eine Wahrscheinlichkeitsverteilung der möglichen Positionen beschrieben wird, wird er im Quantum Walk als eine Superposition von Positionen beschrieben.

Ähnlich wie beim klassischen Random Walk unterscheidet man zwei Arten von Quantum Walks: den diskreten und den kontinuierlichen.

Motivation

Quantum Walks sind motiviert durch den weit verbreiteten Einsatz von klassischen Random Walks im Design randomisierter Algorithmen. Sie sind ein Bestandteil mehrerer Quantenalgorithmen. Bei einigen Orakel-Problemen sind Quantum Walks exponentiell schneller als jeder klassische Algorithmus.[1][2] Für viele praktische Probleme liefern Quantum Walks auch polynomielle Beschleunigungen gegenüber klassischen Algorithmen, zum Beispiel für das Element-Distinctness-Problem (das Problem festzustellen, ob eine Liste Duplikate enthält),[3] dem Problem, zu bestimmen, ob ein Graph dreiecksfrei ist[4] und bei der Evaluierung von NAND-Bäumen. Der wohlbekannte Grover-Algorithmus kann ebenfalls als Quantum Walk betrachtet werden.

Beziehung zum klassischen Random Walk

Quantum Walks unterscheiden sich in ihrem Verhalten deutlich von klassischen Random Walks. Insbesondere konvergieren sie nicht zu einer Wahrscheinlichkeitsverteilung. Aufgrund des Einflusses von Quanteninterferenz können sie sich signifikant schneller oder langsamer verteilen.

Kontinuierlicher Walk

Unter bestimmten Umständen können kontinuierliche Quantum Walks ein Modell für universelle Quantenberechnungen liefern. Dies impliziert nicht notwendigerweise Uniformität.[5]

Diskreter Walk

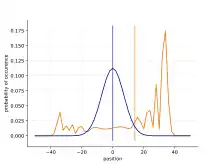
Wahrscheinlichkeitsverteilungen eindimensionaler diskreter Random Walks nach 50 Zeitschritten. Der Quantum Walk, erzeugt mit der Hadamard-Münze, ist in rot, der klassische Walk in blau eingezeichnet.

Ein diskreter Quantum Walk wird durch eine Münze und einen Verschiebungsoperator spezifiziert, die wiederholt angewendet werden. Das folgende Beispiel soll dies illustrieren.[6] Man stelle sich ein Partikel mit einem Spinfreiheitsgrad eines Spin- ${\frac {1}{2}}$ -Teilchens auf einer Linie (einem eindimensionalem Modell) vor. Sein Zustand kann als Produkt eines Spinzustandes $|s\rangle \in {\mathcal {H}}_{C}=\{\left|{\mathord {\uparrow }}\right\rangle ,\left|{\mathord {\downarrow }}\right\rangle \}$ (Eigenzustände der z-Komponente des Spin-Operators mit Eigenwert ${\frac {1}{2}}$ („Spin hoch“) und $-{\frac {1}{2}}$ („Spin runter“)) und einer Spinposition $|i\rangle \in {\mathcal {H}}_{P}=\{|n\rangle :n\in \mathbb {Z} \}$ beschrieben werden. Bei dem Produkt dieser Zustände handelt es sich um das Kronecker-Produkt, welches die beiden Freiheitsgrade separiert. Der Raum der Spinzustände wird Münzraum genannt. Ein bedingter Sprung des Partikels auf der Linie wird durch folgenden Operator beschrieben: $S=\left|{\mathord {\uparrow }}\right\rangle \left\langle {\mathord {\uparrow }}\right|\otimes \sum \limits _{i}|i+1\rangle \langle i|+\left|{\mathord {\downarrow }}\right\rangle \left\langle {\mathord {\downarrow }}\right|\otimes \sum \limits _{i}|i-1\rangle \langle i|$ . Das Partikel springt bei Spin hoch also nach rechts und bei Spin runter nach links. Wendet man beispielsweise die bedingte Sprungoperation auf einem Initialzustand $\left|{\mathord {\uparrow }}\right\rangle \otimes |0\rangle$ an, führt das zum Zustand $\left|{\mathord {\uparrow }}\right\rangle \otimes |1\rangle$ . Rotiert man den Spin zuerst mithilfe einer unitären Transformation $C$ in ${\mathcal {H}}_{C}$ , und wendet dann $S$ an, erhält man eine zufällige Bewegung auf der Linie. Als Transformation kann zum Beispiel die Hadamard-Münze gewählt werden: $\left|{\mathord {\uparrow }}\right\rangle \otimes |0\rangle \;\,{\overset {H}{\longrightarrow }}\;\,{\frac {1}{\sqrt {2}}}(\left|{\mathord {\uparrow }}\right\rangle +\left|{\mathord {\downarrow }}\right\rangle )\otimes |0\rangle \;\,{\overset {S}{\longrightarrow }}\;\,{\frac {1}{\sqrt {2}}}(\left|{\mathord {\uparrow }}\right\rangle \otimes |1\rangle +\left|{\mathord {\downarrow }}\right\rangle \otimes |-1\rangle )$ . Wenn der Spin zu diesem Zeitpunkt gemessen wird, erhält man entweder einen Spin hoch an der Stelle 1 oder einen Spin runter an der Stelle -1. Wiederholte Anwendung der Prozedur würde einem klassischen Walk entsprechen, zum Beispiel einem Galtonbrett. Die Idee des Quantum Walk ist allerdings, zwischen den Wiederholungen der Spin-Rotation und des bedingten Springens nicht zu messen (sodass kein Kollaps der Wellenfunktion stattfindet). Auf diese Weise bleibt die Quantenverschränkung erhalten (d. h. die nicht kollabierten Wellenfunktionen) und verschiedene Positionen können miteinander interferieren. Dies führt zu einer drastisch unterschiedlichen Wahrscheinlichkeitsverteilung im Vergleich zum klassischen Walk (Gaußverteilung), wie in der Abbildung rechts deutlich wird. Insbesondere ist erkennbar, dass die Verteilung nicht symmetrisch ist: Obwohl die Hadamard-Münze mit gleicher Wahrscheinlichkeit Spin hoch und Spin runter liefert, tendiert die Verteilung nach rechts, wenn initial ein Spin hoch vorliegt. Dieser Effekt lässt sich grob gesprochen dadurch erklären, dass die Hadamard-Münze mehr destruktive Interferenz für Positionen auf Wegen nach links als nach rechts liefert. Eine symmetrische Verteilung ist möglich mithilfe einer geeigneten Münze oder einem Initialzustand wie ${\frac {1}{\sqrt {2}}}(\left|{\mathord {\uparrow }}\right\rangle +\mathrm {i} \left|{\mathord {\downarrow }}\right\rangle )\otimes |0\rangle$ , da die Hadamard-Münze keine komplexen Zahlen einführt, sodass Spin hoch und Spin runter sich hier nicht verschränken.

Siehe auch

Pfadintegral

Einzelnachweise

A. M. Childs, R. Cleve, E. Deotto, E. Farhi, S. Gutmann, and D. A. Spielman, Exponential algorithmic speedup by quantum walk, Proc. 35th ACM Symposium on Theory of Computing, pp. 59–68, 2003, quant-ph/0209131.
A. M. Childs, L. J. Schulman, and U. V. Vazirani, Quantum algorithms for hidden nonlinear structures, Proc. 48th IEEE Symposium on Foundations of Computer Science, pp. 395–404, 2007, arxiv:0705.2784.
Andris Ambainis, Quantum walk algorithm for element distinctness, SIAM J. Comput. 37 (2007), no. 1, 210–239, arxiv:quant-ph/0311001, preliminary version in FOCS 2004.
F. Magniez, M. Santha, and M. Szegedy, Quantum algorithms for the triangle problem, Proc. 16th ACM-SIAM Symposium on Discrete Algorithms, pp. 1109–1117, 2005, arxiv:quant-ph/0310134.
Andrew M. Childs: Universal Computation by Quantum Walk. arxiv:0806.1972
Julia Kempe: Quantum random walks - an introductory overview. In: Contemporary Physics. 44, Nr. 4, 1. Juli 2003, ISSN 0010-7514, S. 307–327. arxiv:quant-ph/0303081. doi:10.1080/00107151031000110776.

Literatur

Julia Kempe: Quantum random walks - an introductory overview. In: Contemporary Physics. 44, Nr. 4, 2003, S. 307–327. arxiv:quant-ph/0303081. bibcode:2003ConPh..44..307K. doi:10.1080/00107151031000110776.
Andris Ambainis: Quantum walks and their algorithmic applications. In: International Journal of Quantum Information. 1, Nr. 4, 2003, S. 507–518. arxiv:quant-ph/0403120. doi:10.1142/S0219749903000383.
Miklos Santha: Quantum walk based search algorithms. In: Th Theory and Applications of Models of Computation (TAMC), Xian, LNCS 4978. 5, Nr. 8, April 2008, S. 31–46. arxiv:0808.0059. bibcode:2008arXiv0808.0059S.
Salvador E. Venegas-Andraca: Quantum walks: a comprehensive review. In: Quantum Information Processing. 11, Nr. 5, 2012, S. 1015–1106. arxiv:1201.4780v2. doi:10.1007/s11128-012-0432-5.
Salvador E. Venegas-Andraca: Quantum Walks for Computer Scientists. Abgerufen am 16. Oktober 2008.

Weblinks

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] A. M. Childs, R. Cleve, E. Deotto, E. Farhi, S. Gutmann, and D. A. Spielman, Exponential algorithmic speedup by quantum walk, Proc. 35th ACM Symposium on Theory of Computing, pp. 59–68, 2003, quant-ph/0209131.

[2] A. M. Childs, L. J. Schulman, and U. V. Vazirani, Quantum algorithms for hidden nonlinear structures, Proc. 48th IEEE Symposium on Foundations of Computer Science, pp. 395–404, 2007, arxiv:0705.2784.

[3] Andris Ambainis, Quantum walk algorithm for element distinctness, SIAM J. Comput. 37 (2007), no. 1, 210–239, arxiv:quant-ph/0311001, preliminary version in FOCS 2004.

[4] F. Magniez, M. Santha, and M. Szegedy, Quantum algorithms for the triangle problem, Proc. 16th ACM-SIAM Symposium on Discrete Algorithms, pp. 1109–1117, 2005, arxiv:quant-ph/0310134.

[5] Andrew M. Childs: Universal Computation by Quantum Walk. arxiv:0806.1972

[6] Julia Kempe: Quantum random walks - an introductory overview. In: Contemporary Physics. 44, Nr. 4, 1. Juli 2003, ISSN 0010-7514, S. 307–327. arxiv:quant-ph/0303081. doi:10.1080/00107151031000110776.