Quadratur des Polygons
Die Quadratur des Polygons oder die Quadratur der geradlinigen Figur ist eine Aufgabe aus der antiken Geometrie. Sie besteht darin, mit den euklidischen Werkzeugen Zirkel und Lineal aus einem gegebenen konvexen oder konkaven Polygon ein Quadrat mit gleich großer Fläche zu zeichnen.
Dieser Artikel behandelt im Folgenden ausschließlich das unregelmäßige Polygon. Die Quadratur des Rechtecks wird ausführlich in einem separaten Artikel beschrieben.
Ausgangssituation
Johann Friedrich Lorenz beschreibt in seinem Buch Euklids Elemente, aus dem Jahr 1781, die Lösung dieser Quadratur in Einer gegebnen geradlinichen Figur, A, ein Quadrat gleich zu machen.[1]
Für die Bearbeitung der Aufgabe werden folgende mathematische Sätze von Euklid herangezogen.
- Umwandlung eines Dreiecks in ein Parallelogramm mit gleich großer Fläche.[2][3]
- Umwandlung einer geradlinigen Figur in ein Parallelogramm mit gleich großer Fläche.[4]
- Der Höhensatz im rechtwinkligen Dreieck.
Zur Umwandlung des Dreiecks MNO siehe auch die Animation.
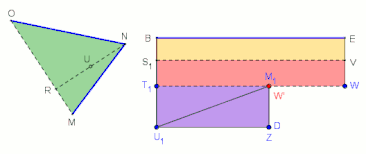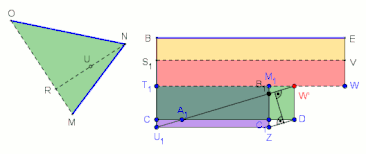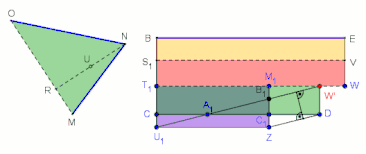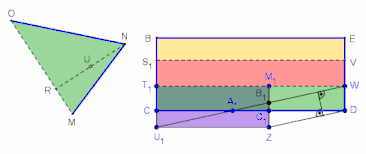
In jedem Schritt stimmen die betroffenen Parallelogramme in einer Seite und der zugehörigen Höhe überein und sind somit jeweils flächengleich:
F(U1ZC1C) = F(U1ZDA1) = F(ZDWB1) = F(C1DWM1)
Methode
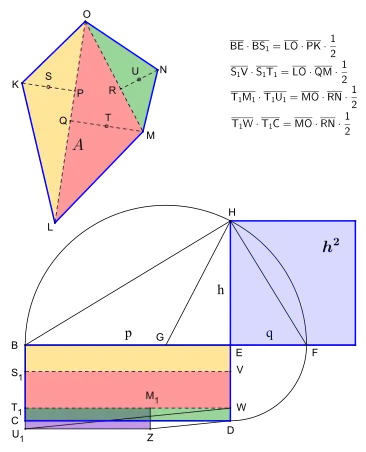
Zur Verdeutlichung der Problematik bei der Quadratur von konvexen Polygonen mit mehr als vier Seiten, wurde das unregelmäßige Fünfeck KLMNO gewählt.
Zuerst wird die Fläche des Polygons in Dreiecke zerlegt, das heißt, ausgehend von einer frei wählbaren Polygonecke, wie z. B. O, werden die Diagonalen gezogen. Es ergibt sich somit die kleinstmögliche Anzahl der Dreiecke; im Beispiel sind es die drei Dreiecke KLO (gelb), LMO (rot) und MNO (grün).
Weiter geht es mit dem Einzeichnen der Dreieckshöhen PK, QM und RN und deren Halbierung; man erhält so die Schnittpunkte S, T und U.
Als Nächstes wird die Diagonale LO (alternativ Diagonale MO) als Strecke BE auf einer Geraden abgetragen.
Aus der Formel zur Bestimmung der Dreiecksfläche für das gelbe Dreieck , a entspricht darin der Diagonale LO und h der Strecke PK, kann die gelbe Rechteckfläche abgeleitet und als F = BE · BS1 konstruiert werden. Dementsprechend gilt dies auch für das rote Dreieck LMO und das rote Rechteck T1WVS1.
Etwas mehr Aufwand verlangt die Umwandlung des grünen Dreiecks MNO, denn dessen Grundlinie MO ist kürzer als die nun zu berücksichtigende Seitenlänge T1W. Nach der ersten Umwandlung des grünen Dreiecks MNO in das rot-blaue Rechteck U1ZM1T1 folgt eine zweite Umwandlung in ein Rechteck mit der Seitenlänge T1W.
Zunächst wird der Punkt U1 mit dem Punkt W verbunden und die Strecke EW etwas verlängert. Eine anschließend konstruierte Parallele zur Strecke U1W ab dem Punkt Z ergibt den Schnittpunkt D.
Die darauffolgende Parallele zur Strecke T1W ab dem Punkt D erzeugt das grüne Rechteck CDWT1 mit der gleich großen Fläche wie das grüne Dreieck MNO;[5] siehe hierzu die Erläuterung in der nebenstehenden Animation Dreieck MNO umgewandelt in ein Rechteck mit gleich großer Fläche bei gegebener Rechteckseite T1W. Für die Veranschaulichung der schrittweisen Umwandlung hat das grüne Dreieck MNO in der Animation eine andere Form.
Die Quadrierung des so zusammengesetzten Rechtecks CDEB beginnt mit der Verlängerung seiner Seite BE und einem Viertelkreis mit dem Radius ED um den Punkt E; damit ergibt sich der Schnittpunkt F.
Nach der Halbierung der Strecke BF im Punkt G, zieht man einen Thaleskreis um G und verlängert die Rechteckseite DE bis zum Thaleskreis; es ergibt sich somit der Schnittpunkt H. Die Strecke EH ist die erste Seite des gesuchten Quadrates, dessen Fläche gleich groß ist, wie die des gegebenen unregelmäßigen Fünfecks.
Weblinks
- Uwe Förster: Prof. Johann Friedrich Lorenz Biografie uni-magdeburg.de
- Zerlegung von Vielecken in Dreiecke (Memento vom 18. Oktober 2016 im Internet Archive) Visuelles Wörterbuch der Mathematik
Einzelnachweise
- Johann Friedrich Lorenz: Euklids Elemente. Band 2. Verlag der Buchhandlung des Waysenhauses, Halle 1781, Abschnitt: Der 14. Satz. Einer gegebnen geradlinichen Figur, A, ein Quadrat gleich zu machen., S. 33 (e-rara.ch [abgerufen am 16. Oktober 2016]).
- Johann Friedrich Lorenz: Euklids Elemente. Erstes Buch. Verlag der Buchhandlung des Waysenhauses, Halle 1781, Abschnitt: Der 42. Satz. Es ist ein Triangel, ABC, gegeben; man soll demselben ein Parallelogramm … gleich machen., S. 21 (e-rara.ch [abgerufen am 16. Oktober 2016]).
- John M. Lee: Construction Problem 16.19 (Parallelogram with the Same Area as a Triangle). In: American Mathematical Society (Hrsg.): Axiomatic Geometry. Rhode Island 2013, S. 302 ff. (books.google.de [abgerufen am 16. Oktober 2016]).
- Johann Friedrich Lorenz: Euklids Elemente. Erstes Buch. Verlag der Buchhandlung des Waysenhauses, Halle 1781, Abschnitt: Der 45. Satz. Es ist eine geradliniche Figur, ABCD, gegeben; man soll derselben ein Parallelogramm … gleich machen., S. 22 ff. (e-rara.ch [abgerufen am 16. Oktober 2016]).
- John M. Lee: Construction Problem 16.20 (Rectangle with a Given Area and Edge). In: American Mathematical Society (Hrsg.): Axiomatic Geometry. Rhode Island 2013, S. 303 ff. (books.google.de [abgerufen am 16. Oktober 2016]).