Polareuklidische Geometrie

Die polareuklidische Geometrie (PEG) ist eine Erweiterung der euklidischen Geometrie. Sie besteht in der Vereinigung der euklidischen Geometrie mit der zu ihr dualen dualeuklidischen Geometrie zu einem Begriffssystem, welches beide Geometrien umfasst und verknüpft und darüber hinaus die Begriffe der klassischen projektiven Geometrie enthält.

Kennzeichnend für die polareuklidische Geometrie ist, dass unter den Punkten der euklidischen Geometrie ein Punkt als „absoluter Mittelpunkte“ (a. M.) ausgezeichnet ist. Auf diesen a. M. stützen sich weitere Begriffe. In der polareuklidischen Geometrie gilt ein Dualitätsprinzip ähnlich wie in der projektiven Geometrie. Innerhalb der PEG können demnach sämtliche Aussagen der gewöhnlichen euklidischen Geometrie dualisiert werden. Die dualisierten Sätze können wiederum innerhalb der euklidischen Geometrie ausgesprochen werden.

Konstruktion

Im Folgenden sei die Konstruktion für die ebene polareuklidische Geometrie kurz erklärt. Ausgangspunkt ist die klassische projektive Geometrie. In ihr wird nun das Begriffssystem sowohl der euklidischen als auch das der dualeuklidischen Geometrie (wie hier beschrieben) etabliert. Dazu wird sowohl eine Gerade als „unendlichferne Gerade“ (u.G.) samt zugehöriger elliptischer Punktinvolution, als auch ein Punkt als „absoluter Mittelpunkt“ (a. M.) samt zugehöriger elliptischer Strahleninvolution ausgezeichnet, wobei der Punkt und die Gerade nicht ineinander liegen mögen. (Die Punkte auf der u.G. heißen Fernpunkte und die Geraden durch den a. M. heißen Nahgeraden.) Entscheidend ist dabei, dass diese beiden Involutionen nicht unabhängig voneinander gewählt werden, sondern so, dass sie Schnitt bzw. Schein voneinander sind. D.h., zwei Nahgeraden sind genau dann einander entsprechende Geraden der Involution im a. M., wenn ihre Fernpunkte sich in der Involution auf der u.G. entsprechen. Mit anderen Worten: Zwei vom a. M. verschiedene Punkte sind genau dann orthogonal, wenn ihre Nahgeraden als euklidische Geraden orthogonal sind.[1][2][3] Die euklidische und die dualeuklidische Geometrie sind so miteinander verknüpft.

In diesem begrifflichen Rahmen, der polareuklidischen Geometrie (PEG), können nun die Aussagen der euklidischen und auch die der dualeuklidischen Geometrie dualisiert werden. Sie werden dann zu Aussagen der jeweils anderen „Teilgeometrie“, können aber, wegen der genannten Verknüpfung auch als Aussagen innerhalb der Geometrie ausgesprochen werden, aus der sie ursprünglich stammen. Insbesondere lassen sich auf diese Weise sämtlich Aussagen der euklidischen Geometrie dualisieren und die dualen Aussagen wiederum innerhalb der euklidischen Geometrie formulieren.[3][4] Darüber hinaus lassen sich Aussagen formulieren, die sowohl Begriffe der euklidischen als auch solche der dualeuklidischen Geometrie enthalten und die sich deshalb in keiner der beiden Geometrien alleine formulieren lassen (siehe Beispiel).

Anmerkungen

Innerhalb der polareuklidischen Geometrie betrachtet man nicht die klassische euklidische Geometrie, sondern die um die unendlichfernen Elemente erweiterte klassische euklidische Geometrie, ihren sogenannten projektiven Abschluss. (Parallelität, Orthogonalität und (damit) die metrischen Begriffe der euklidischen Geometrie sind für die unendlichfernen Elemente nicht definiert.)
Manche Autoren verwenden den Terminus polareuklidische Geometrie für die dualeuklidische Geometrie. Die hier betrachtete polareuklidische Geometrie ist jedoch das Begriffssystem, welches die euklidische und die dualeuklidische Geometrie beide umfasst und in der skizzierten Art miteinander verknüpft.[5]
In der polareuklidischen Geometrie sind sowohl die Sätze der euklidischen, wie die der dualeuklidischen Geometrie formulierbar und gültig und stehen sich dual gegenüber. Beispiele für euklidische oder dualeuklidische Sätze sind deshalb auch Beispiele für polareuklidische Sätze.

Beispiele

In der ebenen polareuklidischen Geometrie sind Punkte und Geraden zueinander dual. Duale Aussagen stellt man traditionell einander in zwei Spalten gegenüber. In der ebenen polareuklidischen Geometrie sind beispielsweise folgende Aussagen dual:

Zwei Geraden sind parallel.	Zwei Punkte sind zentriert.
Zwei Geraden sind orthogonal.	Zwei Punkte sind orthogonal.

Dass zwei Punkte zentriert sind bedeutet, dass sie mit dem a. M. in einer Geraden liegen. Dass sie orthogonal sind heißt, dass sie vom a. M. aus unter einem rechten Winkel erscheinen.

Euklidische Konstruktion des Mittelpunkts und dualeuklidische Konstruktion des Mittelgeraden in der PEG

Mittelpunkt und Mittelgerade

Beispiele für zueinander duale Konstruktionen sind die Konstruktion des Mittelpunkts zweier Punkte in der euklidischen und der dualen Mittelgeraden zweier Geraden in der dualeuklidischen Geometrie.[6] In der PEG kann man die hier angegebene Konstruktion in einem Bild zusammenfassen:

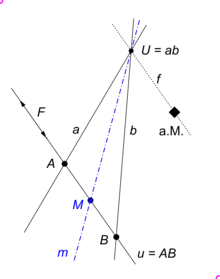
Duale Konstruktion von Mittelpunkt und Mittelstrahl in der PEG

Die linke Konstruktion gehört der euklidischen, die rechte der dualeuklidischen Geometrie an. In der PEG kann man (für Punkte die nicht in der u.G. liegen und Geraden, die nicht durch den a. M. gehen) auch folgendermaßen formulieren:

Der Mittelpunkt $M$ zweier Punkte $A,B$ ist der Schnittpunkt ihrer Verbindungsgerade $u$ mit der Mittelgerade $m$ der beiden Geraden $a$ und $b$ , die einen zum Fernpunkt $F$ von $u$ zentrierter Punkt $U$ mit den Punkten $A$ und $B$ verbinden.	Die Mittelgerade $m$ zweier Geraden $a,b$ ist die Verbindungsgerade ihres Schnittpunktes $U$ mit dem Mittelpunkt $M$ der beiden Punkte $A$ und $B$ , in denen eine zur Nahgeraden $f$ von $U$ parallele Geraden $u$ die Geraden $a$ und $b$ schneidet.

Die Sätze links und rechts greifen auf Begriffe aus der euklidischen und der dualeuklidischen Geometrie zurück und lassen sich deshalb nur in der polareuklidischen Geometrie formulieren.[4]

Schwerpunkt und Leichtgerade

Wie alle anderen euklidischen Konstruktionen lässt sich auch die Konstruktion der euklidischen Schwerlinien und des Schwerpunktes bei einem Dreieck dualisieren.[7] Die für die euklidische und die polareuklidische Geometrie hier getrennt beschriebenen Konstruktionen lassen sich in der polareuklidischen Geometrie als zueinander dual formulieren und dann in einem einzigen Bild darstellen.

Konstruktion von Schwerpunkt und Leichtgerade in der PEG

Die gelben Schwerlinien gehen durch den Schwerpunkt $S$ des Dreiecks $ABC$ und die gelben Leichtpunkte liegen auf der Leichtgeraden $s$ des Dreiseits $abc$ .

Der polareuklidische Kreis

Dual zu einem euklidischen Kreis (einem e-Kreis) ist in der ebenen PEG ein d-Kreis (dualer Kreis), bestehend aus den Tangenten (den d-Kreisgeraden) an einen Kegelschnitt, von dem ein Brennpunkt im a. M. liegt.[8][4] Die aus den Punkten gebildete Kurve dieses Kegelschnitts, also eine Ellipse, Parabel oder Hyperbel, kann man nehmen, um einen d-Kreis zu veranschaulichen. Dual sind dann beispielsweise die Aussagen[9]:

Beispiel für die Dualisierung eines euklidischen Satzes in der polareuklidischen Geometrie

Zwei Tangenten eines e-Kreises bilden mit der Verbindungsgeraden ihrer e-Kreispunkte gleiche Winkel.	Zwei Stützpunkte eines d-Kreises bilden mit dem Schnittpunkt ihrer d-Kreisgeraden gleiche Winkel.

Der rechte Satz besagt in euklidischer Formulierung: Gegeben sei eine Kegelschnittkurve und es sei $F$ (= a.M.) einer ihrer Brennpunkte. Wenn dann $a,b$ die Tangenten in gewissen Kurvenpunkten $A$ und $B$ sind und $C$ ihr Schnittpunkt, dann sind die Winkel $\angle AFC$ und $\angle BFC$ gleich groß.

Dualisierung der euklidischen Satzes, dass Kreise sich unter gleichen Winkeln schneiden.in der PEG

Ein weiteres Beispiel:

Die Tangenten in den beiden Schnittpunkten zweier e-Kreise bilden gleiche Winkel.	Die Stützpunkte in den beiden Verbindungsgeraden zweier d-Kreise bilden gleiche Winkel.

Euklidisch lässt sich die Aussage des rechten Satzes so formulieren: Gegeben zwei Kegelschnitte mit einem gemeinsamen Brennpunkt. Wenn diese Kegelschnitte genau zwei gemeinsame Tangenten haben, dann bilden die beiden Berührpunkte jeder dieser Tangenten mit dem gemeinsamen Brennpunkt gleiche Winkel.[9]

Der Satz des Thales

Im Folgenden sei ein d-Kreis wieder vertreten durch einen Kegelschnitt, in dessen einem Brennpunkt der a. M. liegt. Die zu diesem Brennpunkt gehörende Leitgerade des Kegelschnitts ist dann die Mittelgerade des d-Kreises, das duale Gegenstück zum Mittelpunkt eines (e-)Kreises.[4] Dann kann man links den Satz des Thales und rechts sein duales Gegenstück folgendermaßen formulieren:

Seien $A,B$ zwei Punkte eines e-Kreises, deren Verbindungsgerade durch den e-Kreismittelpunkt $M$ geht. Sei $C$ ein weiterer, beweglicher Kreispunkt. Dann sind die Verbindungsgeraden $AC$ und $BC$ orthogonal zueinander.	Seien $a,b$ zwei Geraden eines d-Kreises, deren Schnittpunkt auf der d-Kreismittelgeraden $m$ liegt. Sei $c$ eine weitere, bewegliche d-Kreisgerade. Dann sind die Schnittpunkte $ac$ und $bc$ orthogonal zueinander.

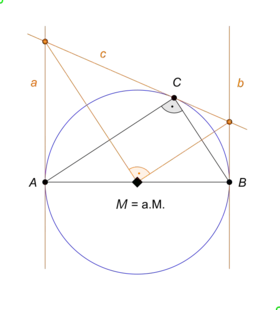
Primaler und dualer Satz des Thales für den Kreis innerhalb der PEG

Innerhalb der dualeuklidischen Geometrie lässt sich der Inhalt der dualen Formulierung rechts auf verschiedene euklidische Sätze über Kegelschnitte spezialisieren:

Nimmt man an, dass die d-Kreismittelgerade die u.G. ist, dann ist der d-Kreis ein gewöhnlicher e-Kreis mit Mittelpunkt im a. M. Der duale Satz des Thales lautet dann:

Es seien $a,b$ parallele Tangenten an einen Kreis und es sei $c$ eine bewegliche dritte Tangente. Dann ist der Winkel, unter dem die beiden Schnittpunkte von $c$ mit $a$ und $b$ vom Mittelpunkt aus gesehen werden, ein rechter.

Im Bild lässt sich dieser Sachverhalt mit dem primalen Satz zusammen darstellen.

Nimmt man dagegen an, es handle sich bei dem d-Kreis um eine euklidische Parabel, dann liegt der a. M. in ihrem Brennpunkt und die u.G. ist eine d-Kreisgerade, also eine Tangente an diese Parabel. Wenn $a$ diese Tangente ist, dann lautet die euklidische Spezialisierung:

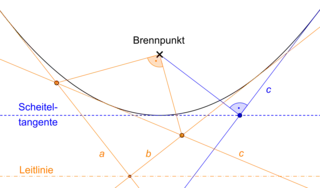
Zwei Varianten der euklidischen Interpretation des dualen Thalessatzes in der PEG

Der Winkel zwischen einer beweglichen Parabeltangente $c$ und der Geraden, die den Brennpunkte mit dem Punkt verbindet, in dem $c$ die Scheiteltangente der Parabel schneidet, ist stets ein rechter.

Wenn alle drei Tangenten $a,b$ und $c$ „gewöhnliche“ Geraden sind, ergibt sich:

Werden zwei feste Tangenten $a,b$ , die sich auf der Leitgerade der Parabel schneiden, von einer dritten, beweglichen Tangente $c$ geschnitten, dann erscheinen die beiden Schnittpunkte vom Brennpunkt aus unter einem rechten Winkel.[9]

Alle diese drei euklidischen Sätze sind Spezialfälle des oben rechts formulierten dualisierten Thalessatzes.[4]

Dualisierung eines euklidischen Parabelsatzes

Eine gewöhnliche Parabel wird im Kontext der PEG auch als e-Parabel bezeichnet. Ihr duales Gegenstück ist dann eine d-Parabel. Der geometrische Ort der Schnittpunkte aller orthogonalen Tangenten an eine Kurve ist deren orthoptische Kurve. Bei der e-Parabel ist das ihre Leitgerade. Das wird in dem folgenden Satz links formuliert, rechts daneben steht die dualisierte Fassung:

Die Schnittpunkte orthogonaler Tangenten einer e-Parabel liegen alle auf einer gemeinsamen Geraden.	Die Verbindungsgeraden orthogonaler Stützpunkte einer d-Parabel gehen alle durch einen gemeinsamen Punkt.

Euklidische Darstellung des Leitpunkt L einer Ellipse bezüglich eines Ellipsenpunktes P

Die u.G. ist Tangente zu einer gewöhnlichen Parabel (e-Parabel). Die zu einer e-Parabel duale d-Parabel besteht also aus den Tangenten an einen Kegelschnitt, zu dessen Punkten der a. M. gehört.[4]

Euklidisch formuliert lautet der obige Satz rechts:

Gegeben sei eine Kurve 2. Ordnung, und ein Punkt $P$ auf der Kurve. Dann gehen die Verbindungsgeraden je zweier Kurvenpunkte, die mit $P$ einen rechten Winkel bilden, durch einen gemeinsamen Punkt $L$ .

Der Punkt müsste sachgemäß der Leitpunkt des Kegelschnitts bezüglich des Punktes $P$ heißen.[4] Im Bild ist der Inhalt des euklidisch formulierten Satzes für den Spezialfall einer Ellipse dargestellt.

Räumliche polareuklidische Geometrie

Die beschriebene Konstruktion der PEG lässt sich auch auf die räumliche Geometrie verallgemeinern. Statt der ausgezeichneten Gerade wird eine ausgezeichnete Ebene, die unendlichferne Ebene eingeführt und dual dazu wieder ein ausgezeichneter absoluter Mittelpunkt a. M. Dual zu euklidischen parallelen Ebenen sind dann zentrierte Punkte, also Punkte, die mit dem a. M. in einer Geraden liegen. Dual zu euklidische parallelen Geraden sind "zentrierte" Geraden: Geraden, die in einer gemeinsamen Ebene liegen, welche auch den a. M. enthält. Dual zu euklidisch orthogonalen Ebenen sind "orthogonale" Punkte, also wie in der ebenen Geometrie Punkte, die vom a. M. unter einem rechten Winkel gesehen werden. Für Geraden gibt es zwei Orthogonalitätsbegriffe: den euklidischen und einen dualeuklidischen. Vereinfacht gesagt sind zwei Geraden dualeuklidisch orthogonal, wenn sie vom a. M. aus betrachtet euklidisch orthogonal aussehen.[4]

Literatur

Rainer Burkhardt: Elemente der euklidischen und polareuklidischen Geometrie. Urachhaus, Stuttgart 1986, ISBN 3-87838-952-3. Hier wird die dualeuklidische Geometrie polareuklische genannt.

Immo Diener: Polareuklidische Geometrie. Unendlichferne Peripherie und absoluter Mittelpunkt: Eine duale Erweiterung der klassischen Geometrie. Springer Spektrum, Berlin 2021, ISBN 978-3-662-63300-7.

M. Enders: Die Dualität in der Geometrie des Maßes. In: Zeitschrift für mathematischen und naturwissenschaftlichen Unterricht. Band 62., Nr. 8,. B.G. Teubner, Leipzig / Berlin 1931, S. 337–341.

Felix Klein: Vorlesungen über nicht-euklidische Geometrie. Kapitel VI: Die Einordnung der euklidischen Metrik in das projektive System. Verlag von Julius Springer, Berlin 1928 (online).

Gerhard Kowol: Projektive Geometrie und Cayley-Klein Geometrien der Ebene. Birkhäuser Verlag, Basel 2009, ISBN 978-3-7643-9901-6.

Louis Locher-Ernst: Projektive Geometrie. 2. Auflage. Philosophisch-Anthroposophischer Verlag, Dornach 1980, ISBN 3-7235-0232-6. Zur dualeuklidischen Geometrie (die hier polareuklidisch genannt wird) siehe Kapitel III und VI.

Einzelnachweise

Louis Locher-Ernst: Projektive Geometrie. 2. Auflage. 1980, IV, Axiom R, S. 255ff.
M. Enders: Die Dualität in der Geometrie des Maßes. 1931, S. 338.
Immo Diener: Polareuklidische Geometrie. Springer Spektrum, 2021, Kapitel 3.
Immo Diener: Polareuklidische Geometrie. Springer Spektrum, 2021, Kapitel 4.
Immo Diener: Polareuklidische Geometrie. Springer Spektrum, 2021, Anmerkung 80.
Louis Locher-Ernst: Projektive Geometrie. 2. Auflage. 1980, S. 246 f.
Louis Locher-Ernst: Projektive Geometrie. 2. Auflage. 1980, S. 249 f.
M. Enders: Die Dualität in der Geometrie des Maßes. 1931, S. 339.
M. Enders: Die Dualität in der Geometrie des Maßes. 1931, S. 340.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Louis Locher-Ernst: Projektive Geometrie. 2. Auflage. 1980, IV, Axiom R, S. 255ff.

[:8-2] M. Enders: Die Dualität in der Geometrie des Maßes. 1931, S. 338.

[:1-3] Immo Diener: Polareuklidische Geometrie. Springer Spektrum, 2021, Kapitel 3.

[:0-4] Immo Diener: Polareuklidische Geometrie. Springer Spektrum, 2021, Kapitel 4.

[5] Immo Diener: Polareuklidische Geometrie. Springer Spektrum, 2021, Anmerkung 80.

[6] Louis Locher-Ernst: Projektive Geometrie. 2. Auflage. 1980, S. 246 f.

[7] Louis Locher-Ernst: Projektive Geometrie. 2. Auflage. 1980, S. 249 f.

[8] M. Enders: Die Dualität in der Geometrie des Maßes. 1931, S. 339.

[:6-9] M. Enders: Die Dualität in der Geometrie des Maßes. 1931, S. 340.