Personenstromsimulation
Eine Personenstromsimulation ist die Computersimulation des Ablaufes von Fußverkehr auf der Grundlage eines mathematischen Modells. Personenstromsimulation werden vor allem bei der Berechnung von Evakuierung genutzt, aber auch bei der Planung von Verkehrskapazitäten, Besuchermanagement oder aus kommerziellen Absichten.
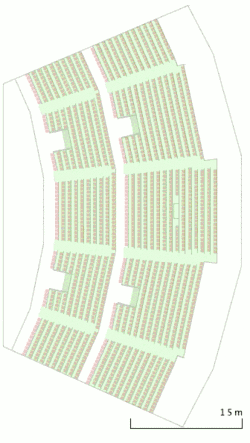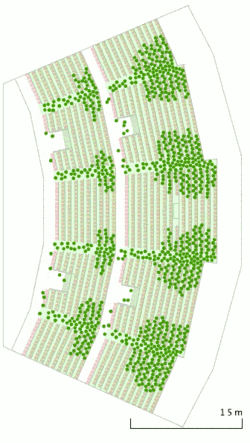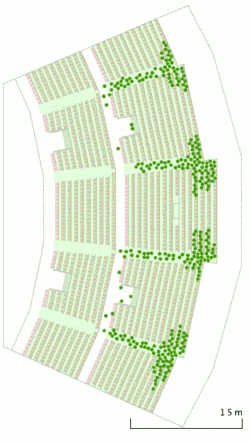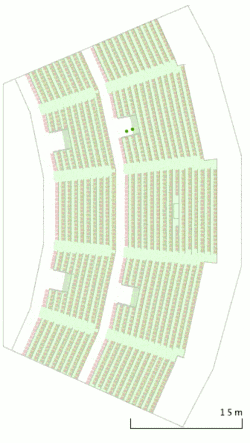
Klassifikation von Modellen
Simulationen sind die Nachbildung der Realität mit Hilfe von mathematischen Modellen und die Berechnung (i. A. mit Computern) von Vorhersagen auf der Grundlage dieser Modelle. Simulationen stellen zunächst keine Optimierungswerkzeuge dar. Um eine Optimierung vornehmen zu können, müssen eine Ergebnisfunktion, die minimiert wird, und eine oder mehrere zu variierende Variablen definiert werden. Modelle lassen sich mit Hilfe folgender Kategorien klassifizieren:[1]
Makroskopisch und mikroskopisch
Mikroskopisch und makroskopische Modelle zur Evakuierungssimulation unterscheiden sich darin, dass makroskopische Modelle übergeordnete, aggregierter Parameter[2] ganzer sich bewegender Menschenmengen abbilden und mikroskopische die individuellen Entscheidungsmöglichkeitern einzelner Menschen mit einberechnen.
Typische makroskopische Modelle sind die sogenannten Netzwerkflussmodelle. Hier wird die Geometrie auf einen Graphen abgebildet und die Personenströme werden als Flüsse auf diesem Graphen betrachtet. Mithilfe von Netzwerkflussalgorithmen können untere Schranken für die Evakuierungszeit ermittelt werden.
Mikroskopischen Modellen beziehen die Interaktion einzelner Individuen mit ein. So verhalten sich Menschen unterschiedlich je nach aktuell möglichen und wahrnehmbaren Bewegungsrichtungen, aktueller Informationslage und persönlicher Erfahrung. Mikroskopische Modelle können auch Phänomene wie Bahnenbildung, da Menschen anderen nach folgen, Staus und Stoßwellen abbilden.
Falls diese autonom sind und interagieren, nennt man sie Agenten und die Modelle Multi-Agenten-Systeme. Stochastische Parameter (üblicherweise der Software-Agenten) dienen der Erfassung nicht näher spezifizierter oder quantifizierbarer Einflüsse (z. B. die Schwierigkeiten bei der räumlichen Orientierung). Diese phänomenologischen Parameter können weder aus anderen direkt messbaren Größen abgeleitet noch in Experimenten direkt gemessen werden. Daher müssen sie anhand von empirischen Untersuchungen kalibriert werden.
Analytische Ergebnisse sind normalerweise für die Berechnung sozialer Systeme nicht möglich. Allgemeine Modelle erlauben die Simulation der Evakuierung von Gebäuden, Flugzeugen und Schiffen gleichermaßen.
Diskret und kontinuierlich

Diskrete Modelle teilen entweder den zu simulierenden Raum in kleine, gleichmäßige, quadratische oder hexagonale Zellen, oder unterteilen die Simulationszeit in berechenbare Abschnitte. Sie unterscheiden sich vor allem in der Granularität. Computergestützte Simulationsmodelle benötigen zwingend eine zeitliche Diskretisierung. Modelle auf Basis von zellulären Automaten nutzen von Natur aus diskrete Räume.[2]
Kontinuierliche Modelle hingegen gehen von einer stetigen Erreichbarkeit jedes Punktes im Raum aus. Kontinuierliche Modelle ermöglichen eine hohe Genauigkeit, benötigen aber nach jedem Einzelschritt eine Ausschluss von Kollisionen, dass nicht zwei Personen auf der gleichen Stelle stehen. Kontinuierliche Räume sind meist rechenintensiver und werden oft für agentenbasierte Modellen genutzt.
Die Unterscheidung in diskret und kontinuierlich bezieht sich nur auf mikroskopische Modelle.
Agentenbasiert und regelbasiert
Simulationsmodelle können auch nach der Art, wie die Individuen modelliert werden, kategorisiert werden:
- Bei regelbasierten Modellen bewegt sich jeder Fußgänger anhand eines globalen Regelsets.
- Agentenbasierte Modelle geben jedem Fußgänger einen individuellen Handlungsplan und persönliche Eigenschaften.
Während in regelbasierten Modellen Eigenschaften oft an der Geometrie hängen und damit über das Betreten einer bestimmten Fläche das Verhalten der Personen bestimmt wird, werden Eigenschaften in agentenbasierten Modellen mit der Person verknüpft und damit das Verhalten von der Geometrie entkoppelt.[2]
Potentialbasiert und differentialgleichungsbasiert
Um die Bewegungen von Personen zu modellieren, gibt es zwei grundlegende Ansätze. Beide Ansätze unterstellen der Masse an Personen, dass alle gewissen "sozialen" Kräften unterliegen. Jede Person verspürt eine Anziehungskraft zum Ziel sowie Abstoßungskräfte von anderen Personen und Hindernissen auf ihrem Weg zum Ziel.
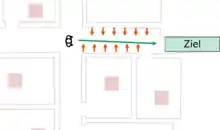
In potentialbasierten Modellen werden diese Kräfte in ein Gradientenfeld überlagert, entlang dessen die Personen laufen. Dabei liegt das Minimum des Potentialfelds in ihrem Ziel, und die Personen laufen entlang des Gradienten des Feldes
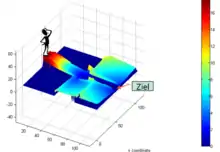
Differentialgleichungsbasierte Modelle überlagern die einzelnen Kräfte in Kraftfelder. Die jeweiligen Kraftfelder werden in einem gemeinsamen Kraftfeld überlagert, entlang dem die Fußgänger in Richtung Ziel laufen.
Damit wird der nächste Schritt des Fußgängers anhand der auf ihn wirkenden Kräften gesteuert. Die darunterliegende Differentialgleichung muss zu jeder Zeit erfüllt sein. Ein spontanes Stoppen einer Person ist so nicht möglich.[2]
Anwendung: Evakuierungssimulation
Die Unterscheidung zwischen der Simulation von Fußgängern in Gebäuden, auf Schiffen und Fahrzeugen auf der einen und Siedlungen oder Gebieten auf der anderen Seite spielt für die Simulation von Evakuierungsprozessen eine wesentliche Rolle.

Gebäude oder Fahrzeuge
Gebäude (Bahnhöfe, Stadien usw.), Schiffe, Flugzeuge und Züge haben im Hinblick auf ihre Evakuierung gemeinsam, dass sich die Personen in erster Linie zu Fuß bewegen. Hinzu kommt die Bewegung auf Notrutschen oder Ähnlichem bzw. bei Schiffen das Zuwasserlassen der besetzten Boote mit Hilfe von Davits. Diese werden zusammenfassend als Evakuierungssystem bezeichnet.
Fahrgastschiffe
Drei besondere Aspekte kennzeichnen die Evakuierung von Schiffen:
- das Verhältnis der Anzahl von Fahrgästen zur Anzahl der Besatzungsmitglieder,
- die Schiffsbewegung,
- die Bedienung und Benutzung der Rettungsmittel.
Die Bewegung des Schiffes beeinträchtigt die Mobilität der Personen an Bord. Hierzu gibt es eine Reihe von Untersuchungen, die über entsprechende Geschwindigkeitsreduktionsfaktoren in einer Simulation berücksichtigt werden können.
Ähnliches gilt für die Rolle der Besatzung bei einer Evakuierung. Allerdings ist dieser Einfluss schwieriger zu quantifizieren, so dass dieser Faktor üblicherweise durch das Verhalten der Fahrgäste (schnellere Orientierung oder Reaktion auf den Alarm) berücksichtigt wird. Dieser Zusammenhang bedarf wiederum einer Kalibrierung durch empirische Untersuchungen. Falls nur quantitative Ergebnisse vorliegen, kann der Einfluss der Besatzung im Sinne einer "Annahme des schlechtesten Falles" (worst case analysis) ganz vernachlässigt werden.
Die Evakuierung eines Schiffes besteht aus zwei getrennten Phasen: der Sammlungs- und der Einbootungsphase. Dies spiegelt sich auch in der Simulation wider. Die Dauern für das Bereitmachen und Besteigen der Rettungsmittel (Boote oder Rettungsflöße bzw. -inseln, die über Rutschen erreicht werden) und das Zuwasserlassen fließen als zusätzliche Parameter in die Simulation mit ein. D. h., der gesamte Ablauf der Evakuierung wird simuliert. Zwar stellen die Rettungsboote keinen endgültig "sicheren Ort" dar. Dennoch betrachtet man die Evakuierung eines Schiffes mit der Entfernung der Boote (bzw. Flöße oder Inseln) aus der Gefahrenzone als abgeschlossen. Die Wiederaufnahme der Personen auf andere Schiffe wird als ein getrennter Prozess betrachtet.
Flugzeuge
Eine Regelung der internationalen Luftfahrtbehörde (International Civil Aviation Organization [ICAO]) schreibt für die Evakuierungsdauer von Flugzeugen eine Obergrenze von 90 Sekunden vor. Diese muss vor der Zulassung eines Flugzeugtyps nachgewiesen werden. Das geschieht entweder mit Hilfe eines Modells oder auf der Grundlage von Analogien zu bereits zugelassenen Flugzeugtypen.
Bei der Simulation der Evakuierung von Flugzeugen sind – wie bei Schiffen – die Dauer für die Bereitstellung der Rettungsrutschen und die Kapazität der Türen bzw. Notrutsche (individuelle Rutschdauer) zu berücksichtigen. Eine Unterscheidung zwischen Sammel- und Rutschphase ist allerdings nicht notwendig, da die Personen unmittelbar zum Notausgang gehen und sofort die Notrutsche besteigen. Die Besatzung spielt dabei eine entscheidende Rolle, da sie für die Bereitstellung der Rettungsmittel verantwortlich ist und die Passagiere aktiv unterstützt (z. B. auf die Rutsche schiebt).
Gebiete (Siedlungen)
Es gibt einen fließenden Übergang von Bürokomplexen, Stadien, Wohnblocks hin zu ganzen Stadtvierteln. Eine Möglichkeit der Unterscheidung im Zusammenhang mit Simulationen ist der Transportmodus: die Bewegung zu Fuß auf der einen und die Benutzung von Transportmitteln (Fahrzeugen oder Hubschrauber) auf der anderen Seite. Solche Prozesse werden aufgrund ihrer Größe und Heterogenität üblicherweise mit Warteschlangenmodellen simuliert.
Die zweite Phase bei der Evakuierung von Gebieten (der Transport von Personen mit Fahrzeugen) kann z. B. mit Hilfe von Warteschlangenmodellen simuliert werden. Da es sich hier um großräumige Simulationen handelt, werden dafür bislang keine mikroskopischen Modelle eingesetzt.
Referenzen
Literatur
- Schadschneider et al. "Evacuation Dynamics: Empirical Results, Modeling and Applications" in R A Meyers (editor) Springer Encyclopedia of Complexity and System Science Springer PDF
Einzelnachweise
- Gershenfeld, Neil: Mathematical Modelling. OUP, Oxford, 1999.
- Angelika Kneidl: Methoden zur Abbildung menschlichen Navigationsverhaltens bei der Modellierung von Fußgängerströmen
Weblinks
- RiMEA - Richtlinie für mikroskopische Entfluchtungsanalysen, Offenes Projekt zur Entwicklung einer Richtlinie für den Gebäudebereich
- traffgo-ht.de - Bibliographie Literaturübersicht zur Simulation von Menschenmengen und Evakuierungsprozessen