Papyrus Moskau 4676

Der Papyrus Moskau 4676 (auch Moskauer Papyrus oder Mathematischer Papyrus Moskau) ist ein altägyptischer Papyrus mit mathematischem Inhalt, der eine Sammlung von insgesamt 25 Rechenaufgaben enthält. Er ist 5,44 m lang und nur 8 cm breit, wird etwa auf das Jahr 1850 v. Chr. datiert und ist neben dem Papyrus Rhind eine der wichtigsten historischen Quellen für die antike ägyptische Mathematik. Er ist von den nunmehr in Moskau befindlichen Papyri der bekannteste und bekam daher diese Bezeichnung.

Detail des Papyrus Moskau (Aufgabe 14), oben Original in Hieratischer Schrift, unten Transkription in Hieroglyphen

Entdeckungsgeschichte

Dieser Papyrus wurde 1893 von dem Ägyptologen Wladimir Semjonowitsch Golenischtschew in Ägypten angekauft und stammt ursprünglich aus Dra Abu el-Naga bei Theben.[1] Der russische Ägyptologe unternahm insgesamt 60 Ägyptenreisen, auf denen er selbst keine eigenen Grabungen durchführte, und verkaufte im Jahre 1911 seine gesammelten Antiquitäten einschließlich des Papyrus Moskau dem Puschkin-Museum für bildende Künste in Moskau, wo es sich noch heute mit der Inventarnummer 4676 befindet.[2]

Inhalt

Der Papyrus ist in hieratischer Schrift niedergeschrieben, deren Übersetzung 1930 von Wassili Wassiljewitsch Struwe und Boris Alexandrowitsch Turajew veröffentlicht wurde.[3]

Der Papyrus enthält 25 mathematische Aufgaben, die nicht so systematisch angeordnet sind, wie beispielsweise im Papyrus Rhind. Deshalb sieht Gabriele Höber-Kamel den Papyrus Moskau als eine Art „Prüfungsarbeit“ und untermauert diese Hypothese einerseits mit der – im Vergleich zu anderen mathematischen Papyri – relativ geringen Aufgabenanzahl und andererseits durch die vorhandene Zusatzbemerkung hinter den Aufgaben, die übersetzt in etwa lautet: „Du hast richtig herausgefunden.“[4]

Die Rechenaufgaben umfassen zumeist Probleme mit einer Unbekannten, die sogenannte Hau-Rechnung.

Die ägyptischen Hieroglyphen

,

anfänglich als „Hau“ transliteriert und mit ḥˁ.w transkribiert (jedoch „Aha(u)“ in moderner Zeichenlesung[5] ˁḥˁ[.w]), bedeutet Haufen; Fülle; Reichtum oder Größe im mathematischen Sinne und ist der altägyptische Terminus für die Unbekannte in einer Berechnung. Es ist jeweils außer einer knappen Aufgabenstellung ein Rechenweg mit konkreten Zahlen angegeben. Vier Aufgaben sind geometrischer Natur.[6]

Aufgabe 6

Aufgabe 6 stellt die Frage nach den Seiten eines Rechtecks mit gegebener Fläche (12) und gegebenem Seitenverhältnis (3 zu 4). Die Lösung benötigt die Bestimmung einer ganzzahligen Quadratwurzel.[7]

Aufgabe 10

eine Kugel aufgeteilt in zwei Halbkugeln

Diese Aufgabe behandelt die Berechnung einer Korboberfläche. Aufgrund von Lücken im Text und der Mehrdeutigkeit des Symbols für "Korb" ist die exakte Deutung jedoch umstritten. In der Fachliteratur finden sich unter anderem Deutungen als Oberfläche einer Halbkugel, eines Halbzylinders oder auch eines korbähnlichen Vorratsbehälters[8]. Unabhängig von der genauen Deutung stellt die Aufgabe aber in jedem Fall eines der ältesten schriftlichen Zeugnisse der näherungsweisen Berechnung einer krummlinigen Oberfläche dar. Die im Folgenden angegebene Beschreibung geht von einer Deutung als Halbkugel aus.

Aus dem Originaltext dieser Aufgabe[9] ergibt sich folgende Berechnungsformel, wobei die Größe d für den Öffnungsdurchmesser des Korbes und damit den Durchmesser des Halbkugelbodenkreises steht:

A=2\times d\times {\frac {8}{9}}\times {\frac {8}{9}}\times d={\frac {128}{81}}d^{2}

Im Vergleich dazu die nach heutiger Erkenntnis korrekte Formel für die Berechnung einer Halbkugeloberfläche:

A={\frac {1}{2}}\pi d^{2}

mit

\pi \approx 3{,}14159\ldots

Das heißt, die Formel entspricht einer Verwendung des folgenden Näherungswertes für die Kreiszahl π (Pi):

\pi \approx {\frac {256}{81}}=3+{\frac {1}{9}}+{\frac {1}{27}}+{\frac {1}{81}}\approx 3{,}16049\ldots

Aufgabe 14

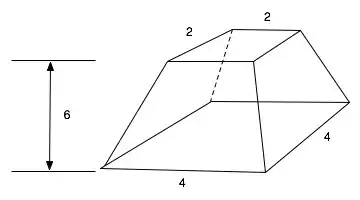
Berühmt ist die Aufgabe 14, in der das Volumen eines quadratischen Pyramidenstumpfs bestimmt wird.[10] Die verwendete Formel ist korrekt und lautet in moderner Schreibweise:

$V={\frac {1}{3}}h(a^{2}+ab+b^{2}),$

wenn a und b die Seitenlängen des Grund- und Deckquadrates sind und h die Höhe. In der Aufgabe wird konkret mit den Zahlen a=4, b=2 und h=6 gerechnet:

$V={\frac {1}{3}}6(4^{2}+4\times 2+2^{2})$

Damit ergibt sich ein Volumen von 56.[11]

Literatur

Wassili Wassiljewitsch Struwe, Boris Turajew: Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau (= Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik, Abteilung A.Bd. 1). Springer, Berlin 1930.
Hans Wußing: 6000 Jahre Mathematik. Springer, Berlin u. a. 2008, ISBN 978-3-540-77189-0, S. 119–121.
Hans Wußing, Wolfgang Arnold (Hrsg.): Biographien bedeutender Mathematiker. Volk und Wissen, Berlin 1975. Lizenz-Nr. 203 1000/74 (E 00 25 05 - 1)

Weblinks

John J. O’Connor, Edmund F. Robertson: Mathematics in Egyptian Papyri. In: MacTutor History of Mathematics archive.
Papyrus Moskau 4676 bei www.meritneith.de (Memento vom 8. August 2013 im Internet Archive)

Einzelnachweise

Heinz-Wilhelm Alten: 4000 Jahre Algebra. Springer, Heidelberg 2003, S. 12.
Guy Rachet: Lexikon des Alten Ägypten. (Memento des Originals vom 15. Januar 2010 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 Neuausgabe, Patmos, 2002, ISBN 978-3-491-69049-3.
Wassili Wassiljewitsch Struwe & Turajew (Hrsg.): Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau. (= Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik, Abteilung A. Quellen 1). J. Springer, Berlin 1930.
Gabriele Höber-Kamel: Astronomie im Alten Ägypten. In: Kemet 4/2000
http://aaew.bbaw.de/tla/servlet/s0?f=0&l=0&ff=14&hc=M35&l1=0
Marshall Clagett: Ancient Egyptian Science: Ancient Egyptian mathematics. 1999. S. 105 ff.
Gericke: Mathematik in Antike und Orient. S. 62.
Hans Wußing: 6000 Jahre Mathematik. Springer, Berlin u. a. 2008, ISBN 978-3-540-77189-0, S. 119–121, (eingeschränkte Online-Version (Google Books)).
Scott W. Williams: Egyptian Mathematical Papyri. Originaltext und Übersetzung der Aufgabe 10 des Papyrus Moskau
http://www.math.buffalo.edu/mad/Ancient-Africa/egypt_moscow14.html Originaltext der Aufgabe 14 des Papyrus Moskau
Helmuth Gericke: Mathematik in Antike und Orient. Springer, 1984, S. 63.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Heinz-Wilhelm Alten: 4000 Jahre Algebra. Springer, Heidelberg 2003, S. 12.

[2] Guy Rachet: Lexikon des Alten Ägypten. (Memento des Originals vom 15. Januar 2010 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 Neuausgabe, Patmos, 2002, ISBN 978-3-491-69049-3.

[3] Wassili Wassiljewitsch Struwe & Turajew (Hrsg.): Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau. (= Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik, Abteilung A. Quellen 1). J. Springer, Berlin 1930.

[4] Gabriele Höber-Kamel: Astronomie im Alten Ägypten. In: Kemet 4/2000

[5] ttp://aaew.bbaw.de/tla/servlet/s0?f=0&l=0&ff=14&hc=M35&l1=0

[6] Marshall Clagett: Ancient Egyptian Science: Ancient Egyptian mathematics. 1999. S. 105 ff.

[7] Gericke: Mathematik in Antike und Orient. S. 62.

[8] Hans Wußing: 6000 Jahre Mathematik. Springer, Berlin u. a. 2008, ISBN 978-3-540-77189-0, S. 119–121, (eingeschränkte Online-Version (Google Books)).

[9] Scott W. Williams: Egyptian Mathematical Papyri. Originaltext und Übersetzung der Aufgabe 10 des Papyrus Moskau

[10] ttp://www.math.buffalo.edu/mad/Ancient-Africa/egypt_moscow14.html Originaltext der Aufgabe 14 des Papyrus Moskau

[11] Helmuth Gericke: Mathematik in Antike und Orient. Springer, 1984, S. 63.