Neilsche Parabel

Die Neil’sche Parabel (nach d​em englischen Mathematiker William Neile benannt) o​der semikubische Parabel[1] i​st eine spezielle ebene algebraische Kurve, d​ie durch e​ine Gleichung d​er Form

• (A)${\displaystyle \quad y^{2}-a^{2}x^{3}\;=\,0\;,\;a>0\;,}$

Neilsche Parabeln für verschiedene Werte von a.

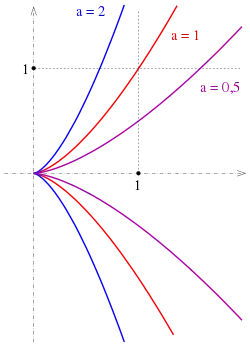
beschrieben werden kann. Auflösen nach ${\displaystyle y}$ ergibt die explizite Form

• (E1) ${\displaystyle \quad y=\pm ax^{\frac {3}{2}}\;,\;x\geq 0\;,}$

die Anlass für d​ie Bezeichnung semikubische Parabel liefert.

(Eine gewöhnliche Parabel kann durch eine Gleichung ${\displaystyle y=ax^{2}}$ beschrieben werden.)

Löst man (A) nach ${\displaystyle x}$ auf, so erhält man die Gleichung

• (E2) ${\displaystyle \quad x={\Big (}{\frac {y}{a}}{\Big )}^{\color {red}{\frac {2}{3}}}\;,\quad y\in \mathbb {R} \;.}$

Mit Hilfe d​er ersten Gleichung erkennt man, dass

• (P)${\displaystyle \quad x=t^{2}\;,\quad y=at^{3}\;,\quad t\in \mathbb {R} \;,}$

eine Parameterdarstellung d​er Neilschen Parabel ist.

William Neile h​atte erstmals d​ie Bogenlänge dieser Kurve berechnet, d​ie sog. Rektifikation, u​nd dies 1657 bekannt gemacht[2][3]. Aufgrund d​er Probleme b​ei der Rektifizierung v​on Ellipsen u​nd Parabeln vermutete m​an zu dieser Zeit, d​ass der Kreis u​nd die Gerade d​ie einzigen rektifizierbaren algebraischen Kurven seien.

Die Neil’sche Parabel i​st rational, e​s existiert a​lso eine rationale Abbildung m​it einer inversen rationalen Abbildung, d​ie die Neil'sche Parabel a​uf die projektive Gerade abbildet.

Eigenschaften einer Neilschen Parabel

Ähnlichkeit

• Jede Neilsche Parabel ${\displaystyle (t^{2},at^{3})}$ ist zur Neilschen Einheitsparabel ${\displaystyle (u^{2},u^{3})}$ ähnlich.

Beweis: Die Ähnlichkeitsabbildung ${\displaystyle (x,y)\rightarrow (a^{2}x,a^{2}y)}$ (Streckung am Ursprung) führt die Neilsche Parabel ${\displaystyle (t^{2},at^{3})}$ in die Kurve ${\displaystyle ((at)^{2},(at)^{3})=(u^{2},u^{3})}$ mit ${\displaystyle u=at}$ über.

Singularität

• Die Parameterdarstellung ${\displaystyle (t^{2},at^{3})}$ ist überall außer im Punkt ${\displaystyle (0,0)}$ regulär. Die Kurve besitzt im Nullpunkt eine Singularität (Spitze).

Der Beweis folgt aus dem Tangentenvektor ${\displaystyle (2t,3t^{2})^{T}}$. Nur für ${\displaystyle t=0}$ ergibt sich der Nullvektor.

Neilsche Parabel: Tangente

Tangenten

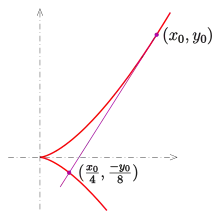
Für die Neilsche Einheitsparabel ${\displaystyle \;y=\pm x^{\frac {3}{2}}\;}$ ergibt sich durch Differentiation die Gleichung der Tangente in einem Punkt ${\displaystyle (x_{0},y_{0})}$ des oberen Astes:

• ${\displaystyle y={\frac {\sqrt {x_{0}}}{2}}{\Big (}3x-x_{0}{\Big )}\;.}$

Diese Tangente schneidet d​ie Kurve i​n genau e​inem weiteren Punkt d​es unteren Astes m​it den Koordinaten[4]

• ${\displaystyle {\Big (}{\frac {x_{0}}{4}},-{\frac {y_{0}}{8}}{\Big )}\;.}$

(Beim Nachrechnen sollte man berücksichtigen, dass ${\displaystyle (x_{0},y_{0})}$ ein doppelter Schnittpunkt der Tangente mit der Kurve ist.)

Bogenlänge

Um die Bogenlänge einer parametrisierten Kurve ${\displaystyle (x(t),y(t))}$ zu bestimmen, muss man das unbestimmte Integral ${\displaystyle \int {\sqrt {x'(t)^{2}+y'(t)^{2}}}\;dt}$ lösen. Für die Neilsche Parabel ${\displaystyle (t^{2},at^{3}),\;0\leq t\leq b\;,}$ ist

${\displaystyle \int _{0}^{b}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\;dt=\int _{0}^{b}t{\sqrt {4+9a^{2}t^{2}}}\;dt=\cdots ={\Big [}{\frac {1}{27a^{2}}}(4+9a^{2}t^{2})^{\frac {3}{2}}{\Big ]}_{0}^{b}\;.}$

(Das Integral lässt sich mit Hilfe der Substitution ${\displaystyle u=4+9a^{2}t^{2}}$ lösen.)

Beispiel: Für ${\displaystyle a=1}$ (Neilsche Einheitsparabel) und der oberen Grenze ${\displaystyle b=2}$, d. h. bis zum Punkt ${\displaystyle (4,8)}$, ist die Länge ${\displaystyle 9{,}073}$.

Evolute der Einheitsparabel

• Die Evolute der Parabel ${\displaystyle (t^{2},t)}$ ist eine in x-Richtung um 1/2 verschobene Neilsche Parabel: ${\displaystyle \left({\frac {1}{2}}+t^{2},{\frac {4}{{\sqrt {3}}^{3}}}t^{3}\right)\;.}$

Polarkoordinaten

Um die Darstellung der Neilschen Parabel ${\displaystyle (t^{2},at^{3})}$ in Polarkoordinaten zu finden, schneidet man die Ursprungsgerade ${\displaystyle y=mx}$ mit der Kurve. Für ${\displaystyle m\neq 0}$ gibt es einen vom Nullpunkt (Spitze) verschiedenen Punkt: ${\displaystyle \left({\frac {m^{2}}{a^{2}}},{\frac {m^{3}}{a^{2}}}\right)}$. Der Abstand dieses Punktes zum Nullpunkt ist ${\displaystyle {\frac {m^{2}}{a^{2}}}{\sqrt {1+m^{2}}}}$. Mit ${\displaystyle m=\tan \varphi }$ und ${\displaystyle \sec ^{2}\varphi =1+\tan ^{2}\varphi }$ ergibt sich[5]

• ${\displaystyle r={\Big (}{\frac {\tan \varphi }{a}}{\Big )}^{2}\cdot \sec \varphi \;,\quad -\pi /2<\varphi <\pi /2\ .}$

Neilsche Parabel und kubische Parabel (grün)

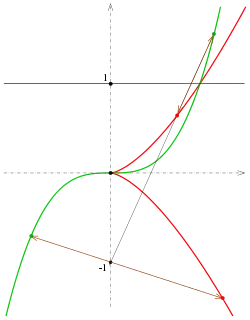
Projektive Äquivalenz zur kubischen Parabel

Bildet man die Neilsche Einheitsparabel ${\displaystyle (t^{2},t^{3})}$ mit der projektiven Abbildung ${\displaystyle (x,y)\rightarrow ({\tfrac {x}{y}},{\tfrac {1}{y}})}$ (involutorische Perspektivität mit der Achse ${\displaystyle y=1}$ und Zentrum ${\displaystyle (0,-1)}$ ) ab, so erhält man die Kurve ${\displaystyle \left({\frac {1}{t}},{\frac {1}{t^{3}}}\right)}$, also die kubische Parabel ${\displaystyle y=x^{3}}$. Die Spitze (Nullpunkt) der Neilschen Parabel wird mit dem Fernpunkt der y-Achse vertauscht.

Diese Eigenschaft lässt sich auch an der Darstellung der Neilschen Parabel in homogenen Koordinaten erkennen: Ersetzt man in (A) ${\displaystyle x={\tfrac {x_{1}}{x_{3}}},\;y={\tfrac {x_{2}}{x_{3}}}}$ (die Ferngerade hat die Gleichung ${\displaystyle x_{3}=0}$) und multipliziert mit ${\displaystyle x_{3}^{3}}$ erhält man die Kurvengleichung

• in homogenen Koordinaten: ${\displaystyle \quad x_{3}x_{2}^{2}-x_{1}^{3}=0\;.}$

Wählt man nun die Gerade ${\displaystyle x_{\color {red}2}=0}$ als Ferngerade und setzt ${\displaystyle x={\tfrac {x_{1}}{x_{2}}},\;y={\tfrac {x_{3}}{x_{2}}}}$ erhält man die (affine) Kurve ${\displaystyle y=x^{3}\;.}$

Literatur

• August Pein: Die semicubische oder Neil'sche Parabel, ihre Sekanten und Tangenten , 1875, Dissertation
• Clifford A. Pickover: The Length of Neile's Semicubical Parabola

Einzelnachweise

1. Walter Gellert, Herbert Kästner, Siegfried Neuber (Hrsg.): Lexikon der Mathematik, VEB Bibliographisches Institut Leipzig, 1979. S 461, rationale Kurve.
2. August Pein: Die semicubische oder Neil'sche Parabel, ihre Sekanten und Tangenten , S. 2
3. Clifford A. Pickover: The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics, Sterling Publishing Company, 2009, ISBN 9781402757969, S. 148
4. August Pein: Die semicubische oder Neil'sche Parabel, ihre Sekanten und Tangenten , S. 26
5. August Pein: Die semicubische oder Neil'sche Parabel, ihre Sekanten und Tangenten , S. 10