Nearest-Neighbor-Heuristik

Die Nearest-Neighbor-Heuristik („Nächster-Nachbar-Heuristik“) ist ein heuristisches Eröffnungsverfahren aus der Graphentheorie und wird unter anderem zur Approximation einer Lösung des Problems des Handlungsreisenden verwendet.

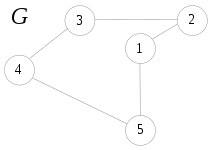
Von einem Knoten als Startpunkt ausgehend wird die minimalgewichtete benachbarte Kante zum nächsten Knoten gewählt. Dieses wird sukzessive fortgesetzt, bis alle Knoten zu einem Hamiltonschen Kreis zusammengefasst wurden. Im Allgemeinen liefert dieser Greedy-Algorithmus nicht die beste Lösung. Dies liegt hauptsächlich daran, dass der Startknoten und der Endknoten zu keinem Zeitpunkt berücksichtigt werden und anstatt dessen eine mögliche große Distanz zwischen ihnen in Kauf genommen wird. In der Tat können Beispiele mit beliebig weit vom Optimum entfernten Lösungen konstruiert werden.[1]

Indem iterativ jeder einzelne Knoten des Graphen jeweils einmal als Startknoten zur Ermittlung der Gewichtung des jeweilig entstehenden Pfades gewählt wird und diese abschließend miteinander verglichen werden, wird das Verfahren besser.

Jedoch entspricht diese All Nearest-Neighbor-Heuristik bereits der Komplexitätsklasse $O(n^{3})$ .

Siehe auch

Einzelnachweise

Lawler, Lenstra, Rinnooy Kan, Shmoys (Hrsg.): The Traveling Salesman Problem. A Guided Tour of Combinatorial Optimization. Wiley, Chichester 1985. ISBN 0-471-90413-9, Abschnitt 5.3.1: Nearest neighbor algorithm

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Lawler, Lenstra, Rinnooy Kan, Shmoys (Hrsg.): The Traveling Salesman Problem. A Guided Tour of Combinatorial Optimization. Wiley, Chichester 1985. ISBN 0-471-90413-9, Abschnitt 5.3.1: Nearest neighbor algorithm