Napoleon-Dreieck
Napoleon-Dreieck, benannt nach dem französischen Feldherrn und Kaiser Napoléon Bonaparte, ist ein Begriff der Dreiecksgeometrie.
Definition
Über den Seiten eines gegebenen Dreiecks ABC werden drei gleichseitige Dreiecke gezeichnet und in diesen jeweils die Geometrischen Schwerpunkte (Flächenschwerpunkte) eingetragen. Das Napoleon-Dreieck entsteht durch Verbinden dieser Schwerpunkte.
Werden die gleichseitigen Dreiecke nach außen gerichtet angelegt, so ergibt die Schwerpunktsverbindung das Äußere Napoleon-Dreieck, bei Anlage der gleichseitigen Dreiecke nach innen hin erhält man das Innere Napoleon-Dreieck.
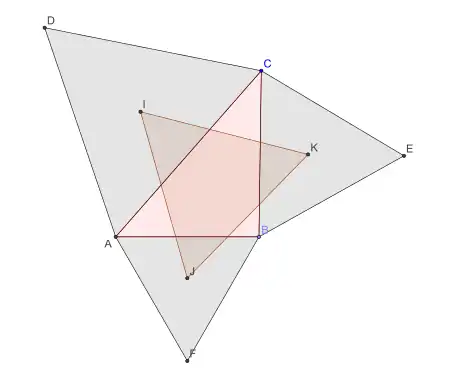
Das Napoleon-Dreieck ist – unabhängig von der Form des ursprünglichen Dreiecks – stets gleichseitig.
Es gibt keine bekannten Hinweise, dass dieser Satz von Napoleon gefunden wurde. In der Zeitschrift „The Ladies’ Diary“ wurde der Satz 1825 von dem britischen Mathematiker William Rutherford erwähnt.[1]
Eigenschaften
Der Schwerpunkt des gegebenen Dreiecks fällt mit dem Schwerpunkt des Äußeren Napoleon-Dreiecks und mit dem Schwerpunkt des Inneren Napoleon-Dreiecks zusammen. Bildet man die Differenz der Flächeninhalte des Äußeren Napoleon-Dreiecks und des Inneren Napoleon-Dreiecks, so erhält man den Flächeninhalt des gegebenen Dreiecks.
Verallgemeinerung
Ersetzt man in der Definition die drei gleichseitigen Dreiecke durch ähnliche gleichschenklige Dreiecke, so spricht man von einem Kiepert-Dreieck.
Literatur
- H. S. M. Coxeter, S. L. Greitzer: Zeitlose Geometrie. Klett, Stuttgart 1983
Weblinks
- Napoleon-Dreieck – eine Visualisierung mit dem dynamischen Geometrieprogramm GeoGebra
- Eric W. Weisstein: Inner Napoleon Triangle. In: MathWorld (englisch).
- Eric W. Weisstein: Outer Napoleon Triangle. In: MathWorld (englisch).
Einzelnachweise
- Ulf von Rauchhaupt: Napoleon’s Theorem. In: FAZ.net. 15. August 2019, abgerufen am 24. April 2021.