Mischungskreuz

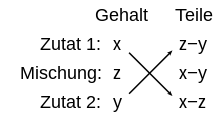
Das Mischungskreuz (auch Andreaskreuz genannt) ist ein Rechenschema für das Mengenverhältnis zweier Zutaten einer Mischung, also die Gewichtsfaktoren im arithmetischen Mittel, für einen gewünschten Mittelwert. Die Kreuzform deutet an, dass von der einen Zutat umso mehr benötigt wird, je weiter der Gehalt der anderen Zutat vom angestrebten Mittelwert abweicht.

Mischungskreuz. Die Gehalte der Zutaten stehen links oben und unten, dazwischen der gewünschte Gehalt der Mischung. Rechts oben und unten stehen Differenzen dieser Gehalte. Deren Zahlenwerte werden als zu verwendende Teilmengen interpretiert.

Oft ist die zu mittelnde Größe der Massenanteil eines Stoffes, seltener die spezifische Partialstoffmenge. Auch kann eine bestimmte Temperatur der Mischung gefordert sein, siehe Richmannsche Mischungsregel. Konzentrationsangaben funktionieren nur, wenn das Volumen beim Mischen konstant bleibt, wie bei idealen Gasen (unter konstantem Druck) oder bei stark verdünnten Lösungen (mit dem gleichen Lösungsmittel).

Herleitung

Beim Mischen zweier Zutaten A und B zu einer Mischung C bleibt die Masse $m$ des interessierenden Stoffes erhalten (rechte und linke Seite der folgenden Gleichung, berechnet aus Massen und Massenanteilen $w$ ):

m_{A}w_{A}+m_{B}w_{B}=(m_{A}+m_{B})w_{C}

Wird diese Gleichung durch die Klammer geteilt, so ergibt sich die Formel für das gewichtete arithmetische Mittel. Für die Umkehrung derselben teilen wir nur durch ${m_{B}}$ und lösen nach ${\frac {m_{A}}{m_{B}}}$ auf:

{\frac {m_{A}}{m_{B}}}={\frac {w_{C}-w_{B}}{w_{A}-w_{C}}}

Zähler und Nenner der rechten Seite stehen im Mischungskreuz rechts oben bzw. unten. Die sich ergebenden Zahlenwerte als Massen $m_{A}$ und $m_{B}$ interpretiert, ergäben eine Gesamtmasse der Mischung entsprechend dem Zahlenwert von $w_{A}-w_{B}$ . Für eine beliebige Gesamtmasse $m_{C}$ kann man normierte Gewichte[1] verwenden:

r_{A}={\frac {m_{A}}{m_{A}+m_{B}}}={\frac {w_{C}-w_{B}}{w_{A}-w_{B}}}

r_{B}=1-r_{A}

Damit ergeben sich die benötigten Massen der Zutaten zu

m_{A}=r_{A}m_{C}

,

m_{B}=r_{B}m_{C}

.

Anwendungen

Schulnoten

Ein einseitig interessierter Schüler hat regelmäßig drei Einsen, in Mathe, Physik und Chemie, sonst nur Dreien und Vieren, abhängig vom Einsatz. Er strebt einen Mittelwert von 3,0 an. Wie viele Vieren darf er sich erlauben? (Die Zahl der Dreien ist nicht relevant für einen Mittelwert von 3,0).

Da der Abstand einer Vier vom Mittelwert (4 − 3 = 1) halb so groß ist wie der Abstand der Einsen vom Mittelwert (3 − 1 = 2), kann er sich doppelt so viele, also sechs Vieren erlauben.

Mischen von Flüssigkeiten

Beispielrechnung 1 (Mischen mit reinem Wasser, d. h., y = 0):
Es soll eine 35-prozentige Säure mit Wasser so gemischt werden, dass sich eine 22-prozentige Säure ergibt. Wie viel Wasser und wie viel Säure werden benötigt?

Die Massenanteile auf der linken Seite sind w = 35 % für die Säure und w = 0 % für das Wasser, in der Mitte steht der Zielwert von 22 %.

${\begin{array}{ccccc}{\text{35}}&{}&{}&{}&22-0=22\\{}&\diagdown &{}&\nearrow &{}\\{}&{}&{\text{22}}&{}&{}\\{}&\diagup &{}&\searrow &{}\\{\text{0}}&{}&{}&{}&35-22=13\end{array}}$

Insgesamt sind es 35 Teile. Es werden folglich 22 Teile der 35-prozentigen Säure und 13 Teile Wasser benötigt, um eine 22-prozentige Säure herzustellen.

Sollen 1000 g der 22-prozentigen Mischung hergestellt werden, benötigt man demnach:

Säure : (1000 g / 35) * 22 = 629 g
Wasser: (1000 g / 35) * 13 = 371 g

Wegen y = 0 reicht ein Dreisatz: 1000 g Säure (unverdünnt) ist 35-prozentig, 22/35*1000 g = 629 g Säure mit Wasser ergänzt auf 1000 g ist 22-prozentig.

Beispielrechnung 2 (Mischen mit 15-prozentiger Säure):
Statt mit Wasser könnte auch mit 15-prozentiger Säure verdünnt werden:

${\begin{array}{ccccc}{\text{35}}&{}&{}&{}&22-15=7\\{}&\diagdown &{}&\nearrow &{}\\{}&{}&{\text{22}}&{}&{}\\{}&\diagup &{}&\searrow &{}\\{\text{15}}&{}&{}&{}&35-22=13\end{array}}$

Bei einem gewünschten Massenanteil von 22 % müssten dann

22 – 15 = 7 Teile 35-prozentige Säure und
35 – 22 = 13 Teile 15-prozentige Säure

gemischt werden, insgesamt 20 Teile.

Für 1000 g der 22-prozentigen Säure benötigt man also

35-prozentige Säure: (1000 g / 20) * 7 = 350 g
15-prozentige Säure: (1000 g / 20) *13 = 650 g

Legierungen

Das Mischungskreuz eignet sich nicht zur Abschätzung der Masseanteile binärer Legierungen über die Dichte. Z.B. sind für Kupfer, Zink und Messing CuZn40 (40 % Zn) Dichten von 8,92 (x), 7,14 (y) bzw. 8,41 (z) angegeben (in g/cm³). Die Berechnung des Zink-Anteils per Mischungskreuz ergibt (x-z)/(x-y) = 29 %. Der Unterschied ist wesentlich: Bis 37 % Zn ist Messing einphasig (α-Struktur), darüber zweiphasig (α+β).

Allgemein

Mischungskreuz

Allgemein eignet sich das Mischungskreuz stets, wenn das gewichtete arithmetische Mittel angemessen, also Linearität gegeben ist. Im kaufmännischen Kontext etwa ist das der Fall für die Kosten der Zutaten einer Mischung. Kosten z. B. zwei Teesorten 26 bzw. 37 €/kg, so lässt sich das Mischungsverhältnis für einen Mittelwert von 34 €/kg wie folgt berechnen:

subtrahiere 26 von 34, ergibt 8 (Teile von der teureren Teesorte),
subtrahiere 34 von 37, ergibt 3 (Teile von der weniger teuren Sorte).

37 − 26 = 8 + 3 = 11 Teile. Das gewichtete arithmetische Mittel lautet dann (in €/kg):

{\tfrac {8}{11}}37+{\tfrac {3}{11}}26=34.

Literatur

Martin Holtzhauer: Biochemische Labormethoden. 3. Auflage. Springer, Berlin / Heidelberg 1997, ISBN 978-3-540-62435-6, S. 288 f. (eingeschränkte Vorschau in der Google-Buchsuche).
Reiner Friebe, Karl Rauscher: Chemische Tabellen und Rechentafeln für die analytische Praxis. 11. Auflage. Verlag Harry Deutsch, Frankfurt am Main 2000, ISBN 978-3-8171-1621-8.

Einzelnachweise

Die Gewichte sollten positiv herauskommen, ggf. nach Kürzen negativer Vorzeichen in Zähler und Nenner (im Fall $w_{A}<w_{B}$ ). Sollte nur der Zähler oder nur der Nenner negativ sein, dann liegt ein Rechenfehler vor oder $w_{C}$ nicht zwischen $w_{A}$ und $w_{B}$ .

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Die Gewichte sollten positiv herauskommen, ggf. nach Kürzen negativer Vorzeichen in Zähler und Nenner (im Fall $w_{A}<w_{B}$ ). Sollte nur der Zähler oder nur der Nenner negativ sein, dann liegt ein Rechenfehler vor oder $w_{C}$ nicht zwischen $w_{A}$ und $w_{B}$ .