Maxwell-Bloch-Gleichungen
Die Maxwell-Bloch-Gleichungen beschreiben die Wechselwirkung eines Ensembles quantenmechanischer Zweiniveausysteme mit einem oszillierenden elektrischen Feld. Sie werden zur Beschreibung von Absorption und Emission von Licht in Festkörpern und Gasen verwendet und spielen insbesondere beim theoretischen Verständnis der Verstärkung in Lasern eine zentrale Rolle. Voraussetzung ist dabei, dass die Energiedifferenz des Übergangs nahe bei der Photonenenergie des Lichts ist und, dass die anderen Übergänge des Systems deutlich andere Übergangsenergien besitzen.
Gleichungen
Die Maxwell-Bloch-Gleichungen lauten
mit:
- : komplexe Amplitude des elektrischen Felds
- : komplexe Amplitude der Polarisation
- : Besetzungsinversion mit und Besetzungszahldichte der Niveaus 1 und 2
- : Zahl der Zweiniveausysteme pro Volumen
- : Frequenz des elektrischen Feldes
- : Frequenz des Übergangs mit
- : Phasenrelaxationszeit, Kohärenzzeit der Polarisation.
- : Lebensdauer des zweiten Zustandes
- Projektion des Dipolübergangsmatrixelement auf die Richtung des elektrischen Feldes
- : Gruppengeschwindigkeit im Medium
- : Magnetische Feldkonstante
- : Phasengeschwindigkeit im Medium
Näherungen
Kohärentes Regime
Im kohärenten Regime nimmt man an, dass die typischen Zeitableitungen von und sehr viel größer als die Zerfallsterme sind, also
gilt. Damit nehmen die Maxwell-Bloch-Gleichungen die Form
an. Man kann leicht zeigen, dass in diesem Fall
gilt. Deshalb liegt die Einführung des sog. Bloch-Vektors
mit nahe. Für diesen gilt die Bewegungsgleichung
mit der sog. Rabi-Frequenz und der Verstimmung .
Im Fall der sog. resonanten Kopplung, d. h. und reell findet man die Gleichungen
Die Lösungen dieses Differentialgleichungssystems lauten
mit der sog. Pulsfläche mit
Somit führen und Schwingungen aus, die vom elektrischen Feld getrieben werden. Dies nennt man Rabi-Oszillationen. Mit der dritten Maxwell-Bloch-Gleichung findet man, unter der Annahme einer dünnen Probe der Länge L, d. h. , für das reemittierte elektrische Feld
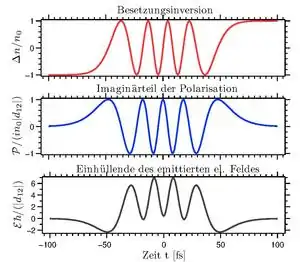
Wenn man nun einen eingehenden Lichtpuls so präpariert, dass mit kann man das Medium vollständig invertieren. Man spricht dann von einem -Puls (siehe Abbildung). Für ist die Besetzungsinversion null und die Polarisation ist maximal. Mit dieser Methode kann man also ein Material in einen genau definierten Zustand bringen.
Herleitung
Zur Herleitung der Maxwell-Bloch-Gleichungen beschreibt man die Wechselwirkung zwischen elektrischem Feld und Atom in der sog. Dipolnäherung. Der Hamilton-Operator des Systems besteht aus zwei Anteilen. Dem Anteil der das Atom ohne Wechselwirkung mit dem elektrischen Feld beschreibt und dem Anteil der eine dipolartige Wechselwirkung zwischen Licht und Atom beschreibt:
mit
Die Wellenfunktion kann in der Basis des ungestörten Systems als
dargestellt werden. Die Schrödingergleichung lautet nun
Durch Multiplikation mit und Einsetzen der Basisdarstellung von folgt
Dabei wurde ausgenutzt. Die mikroskopische Polarisation des Systems ist nun durch
gegeben. Für die zeitlichen Ableitungen der Polarisationskomponenten und folgt
Dabei wurden die Gleichungen
verwendet. Die Gleichung für ergibt sich einfach aus der komplex konjugierten Gleichung.
Für den feldfreien Fall () schwingt die Polarisation nun harmonisch. In realen System klingt die Polarisation allerdings ab, weshalb man einen Zerfallsterm addiert. Die Materialkonstante nennt man dabei Phasenrelaxationszeit. Weiterhin verwendet man die sog. Rotating Wave Näherung. Dabei setzt man
und vernachlässigt in der Gleichung für und entsprechend in der Gleichung für , da die vernachlässigten Terme mit oszillieren und somit im Vergleich zu den Termen mit klein sind. Für die Polarisation folgt somit
was durch den Ansatz noch zu
vereinfacht werden kann. Für die Zeitableitung der Besetzungsinversion folgt
Auch hierbei würde im feldfreien Fall die Besetzungsinversion konstant bleiben, weshalb man einen Term mit addiert.
Dabei ist die mittlere Lebensdauer des angeregten Zustandes. Zuletzt braucht man noch eine Gleichung für das elektrische Feld. Dabei geht man von der Wellengleichung
aus. Durch Einsetzen der schon erhaltenen Zusammenhänge und Ansätze folgt
und damit die letzte Maxwell-Bloch-Gleichung
Literatur
- Dieter Meschede: Optik, Licht und Laser. Vieweg+Teubner Verlag; 3., durchges. Aufl. 2008. ISBN 978-3-8351-0143-2