Mathematische Demografie

Als Mathematische Demografie bezeichnet man das Teilgebiet der Demografie, das Zusammenhänge und Verfahren der Demografie mit mathematischen Mitteln analysiert und begründet. Dabei kommen u. a. mathematische demografische Modelle zur Anwendung.

Untersuchungsobjekte

Die math. Demografie umfasst u. a. die Erstellung und Analyse von:

math. Modellen zu Populationen,
Sterblichkeits- und Fruchtbarkeitsraten,
Abhängigkeiten des Zahlenverhältnisses Frauen zu Männern,
verschiedene Typen von Instabilitäten einer Population.

Weiterhin werden untersucht u. a.:

Ansätze zur Stabilisierung einer Population,
die demografische Theorie der Verwandtschaften, aber auch
Micro-Demografie, z. B.: Geburtenraten – beeinflusst durch Verhütungsmittel, sowie
die Familien-Demografie.

Der Fokus liegt hierbei in der Untersuchung der inneren Zusammenhänge einer Population und weniger auf der Vorhersage einer Bevölkerungsentwicklung.

Beispiel 1: Berechnung der Reproduktionsrate für eine stationäre Bevölkerung

Berechnet werden soll die angenäherte Zahl der Kinder pro Frau, mit denen eine Erhaltung der Bevölkerungsgröße in Form einer stationären Bevölkerung möglich ist. Die Berechnungen basieren auf Daten der USA insbesondere aus dem Jahr 1967.

Die relative Zahl der Geburten, bei der Mädchen zur Welt kommen ist: 0,488. Das bedeutet 48,8 % der Gesamtzahl der Geburten sind Mädchen, basierend auf Daten der USA aus dem Jahr 1967.[1] Im Falle von drei Kindern pro Mutter ergeben sich dann im Mittel: 3 · 0,488 = 1,464 Töchter pro Mutter.
Nicht alle Töchter werden überleben, bis sie sich reproduzieren können. US-Daten aus dem Jahre 1967 ergeben hierbei den Faktor: 0,9665. Im Falle einer 3-Kind-Familie sind das also im Mittel 0,9665 · 1,464 = 0,9665 · (3 · 0,488) = R₀ = 1,415 Töchter pro Frau, die ihre Fruchtbarkeitsphase erreichen.
Ein unbekannter Anteil der Frauen kann oder will keine Kinder haben, nehmen wir hierfür an: 10 %.[1] Dies ergibt dann 1,415 (Töchter pro Mutter) · 0,9 = 1,273 fruchtbare Töchter mit eigenem Kind, pro Frau.

Für den möglichen Fall von durchschnittlich zwei Kindern pro Mutter erhält man dann einen Wert von 2,0 · 0,488 · 0,9665 · 0,9 = R_2,0 = 0,849 als Reproduktionsrate bzw. Ersetzungsfaktor pro Generation (= Töchter mit Kind, pro Mutter). Unter Berücksichtigung einer Generationendauer von 26,14 Jahren (US-Daten für 1967) ergibt sich mit der 26,14ten-Wurzel (26,14 Jahre jeweils der gleiche Faktor r pro Jahr: $r^{26,14}=R_{2,0}$ und man erhält weiter: $r={\sqrt[{26,14}]{R_{2,0}}}$ ) der Ersetzungsfaktor von r = 0,9938 pro Jahr für den Fall von durchschnittlich 2,0 Kindern pro Mutter. Dies entspricht einer Verringerung der Bevölkerung von 0,62 % pro Jahr. Die biologische Halbwertzeit der betroffenen Population liegt dann bei 111 Jahren.

Für den Fall von drei Kindern pro Mutter lässt sich die folgende Gesamtgleichung schreiben:

(1)

3\cdot 0{,}488\cdot 0{,}9665\cdot 0{,}9=R

,

mit R als Reproduktionsrate „fruchtbare Töchter mit eigenem Kind, pro Mutter“. Man erhält für diesen Fall nun: R = 1,273 Töchter mit Kind, pro Mutter. Daraus ergibt sich wiederum ein jährliches Wachstum der Bevölkerung von 0,93 % bei einer mittleren Generationendauer von 26,14 Jahren. Daraus errechnet sich ein Faktor 16 für die neue US-Bevölkerungsgröße in etwas weniger als dreihundert Jahren.

Um die Bevölkerung als stationär erhalten zu können, setzen wir R = R_stationär = 1 (Töchter mit Kind, pro Mutter). Gesucht wird nun der mittlere Wert x₁ Kinder pro Frau, um folgende Gleichung zu erfüllen:

(2)

x_{1}\cdot 0{,}488\cdot 0{,}9665\cdot 0{,}9=R_{\mathrm {station{\ddot {a}}r} }=1

.

Man erhält: x₁ = 2,36 Kinder pro fruchtbare Frau, in diesem Fall (die mittlere endgültige Zahl): Kinder pro Mutter. Der größte Unsicherheitsfaktor hierbei ist die Annahme der 10 % Frauen, die keine Kinder bekommen können oder wollen, siehe obiger Punkt 3.

Mit aktuellen US-Sterberaten und durchschnittlich drei Kindern pro Mutter würde man in dreihundert Jahren eine US-Bevölkerungsgröße von mehr als drei Milliarden Einwohnern erhalten. Was wir benötigen ist jedoch nur ein Mittelwert von 2,36 Kindern pro Mutter, so der Autor (siehe Quelle,[1] S. 426, ca. Zeile 16).

Der oft genannte Wert von 2,1 Kinder pro Frau steht damit in Zusammenhang, und er lässt sich wie folgt berechnen.

Man erhält aus x₂ · 0,488 · 0,9665 = R_stationär = 1 den Wert x₂ = 2,12.

Dieser Wert „2,12 Kinder pro Frau“ beschreibt die mittlere endgültige Kinderzahl pro Frau – einschließlich der Frauen, die lebenslang ohne eigene Kinder bleiben – unter Berücksichtigung von US-Daten aus dem Jahr 1967.[1]

Diese Zahlen zeigen, dass der Mittelwert feinjustiert werden muss; auch kleine Abweichungen können über eine lange Zeit zu intolerablen Abweichungen nach oben oder unten führen, so der Autor (S. 426, ca. Zeile 26).

Beispiel 2: Ansätze zur Stabilisierung einer Bevölkerungsgröße

Auf die theoretische Möglichkeit eines Gleichgewichtsmechanismus für die Größe einer Bevölkerung hat Frisch (1972) hingewiesen.[2] Unterernährte Frauen erreichen die Fruchtbarkeitsphase später und die Menopause früher im Vergleich zu gut ernährten Frauen. Abhängig von der z. B. natürlich bedingten Verfügbarkeit von Nahrung besteht mit diesem Mechanismus die Möglichkeit zur Erhöhung oder Verringerung von Geburtenraten. Jedoch eignet sich dieser Ansatz nicht, um Kurzzeitfluktuationen der Bevölkerungsgröße auszugleichen (Keyfitz/Caswell, S. 427, Zeile 10).[1]

In einer anderen Theorie ergibt sich ein weiterer Ansatz für einen Mechanismus zum Stabilisieren der Bevölkerungsgröße durch eine gesetzliche Anpassung des Mindestheiratsalters. Der Autor der Quelle argumentiert, dass durch dieses gesetzliche Mindestheiratsalter effektiv der jeweilige Teil der Fruchtbarkeitskurve unterhalb des spezifizierten Alters eliminiert wird (Keyfitz/Caswell,[3] S. 504, Zeile 4). Im Beispiel von Indien errechnen sich dabei für das Jahr 1961 mit 18,14 Millionen Geburten ganze 3,24 Millionen Geburten bzw. 18 % der Geburten von Müttern unterhalb von 20 Jahren.[4] Zur Beurteilung der Wirksamkeit einer solchen Anpassung des gesetzlichen Mindestheiratsalters weist der Autor auf die theoretische Möglichkeit hin, dass die ggf. von einer Familie fest gewünschte Kinderzahl dann zwar nicht im persönlichen angedachten Zeitraum umgesetzt werden könnte, aber dennoch mit nur wenigen Jahren Zeitverzögerung.[3]

Ob sich bei festem Mindestheiratsalter bereits ein stabilisierender Mechanismus unter Anwendung einer solchen Fruchtbarkeitskurve ergibt, in dem praktischerweise direkt derjenige, der vom (zumindest in Deutschland durch Art. 6 Abs. 1 des Grundgesetzes besonders geschützten) Familiengeschehen ablenkt, auch zeitgleich, zur Kompensation, in zulässiger Weise hinreichend umfangreich auf bzw. über existierende rechtsgültige Ehe-Gesetze u. a. zum Mindestheiratsalter (z. B. 18 Jahre in der Schweiz,[5] Österreich: ehemündig mit 16 J und darunter (minderjährig) auf Antrag,[6] sonst 18 J) + in (a) größerem oder (b) kleinerem Umfang hinweist und aufklärt, bzw. aufklären muss, ist in Quelle[1] bisher nicht auffindbar. Der Umfang dieser Aufklärung über die Möglichkeiten einer Ehe (ab z. B. 16 Jahre, also bereits während des Schulzeit) wäre dann der mögliche Steuerungsparameter zum Stabilisieren einer Bevölkerungsgröße.

Beispiel 3: Markow-Ketten für individuelle Lebensabläufe

Die Quelle[7] beschreibt einen Lebenszyklus, den ein Individuum durchläuft, von Geburt bis zum Tode, mittels eines mathematischen Modells. Ein solcher Lebenszyklus ist gekennzeichnet u. a. durch verschiedene Ereignisse, die sich dann auch im Modell widerspiegeln können. Einige dieser Ereignisse wie Paarung und Reproduktion sind optional (S. 245, Zeilen 5–6), aber auch Heirat fällt darunter. Andere, wie der Tod, sind unvermeidlich. Ein Ansatz diese Informationen zu handhaben, besteht in der Verwendung von Matrix-Modellen bzw. Markow-Ketten. Diese können die zu beschreibenden Zustände in formal-mathematischer Darstellung beinhalten, aber eben auch die Übergangswahrscheinlichkeiten zwischen diesen Zuständen untereinander.

Lebenszyklus-Graph für einen altersklassifizierenden Lebenszyklus

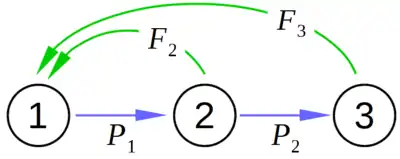
Abb. 1: Einfaches Modell eines Lebenszyklus-Graphen für einen altersklassifizierenden Lebenszyklus. Die mathematischen Zustände werden vereinfacht durch ‚1‘, ‚2‘ und ‚3‘ wiedergegeben. In diesem Modell beschreiben P₁ und P₂ die Übergangswahrscheinlichkeiten in den jeweiligen Folgezustand, sowie F₂ und F₃ die entsprechenden Reproduktionswahrscheinlichkeiten.

Zur Konstruktion eines Matrix-Populations-Modells eignet sich ein sog. Lebenszyklus-Graph. Als Beispiel sei hier ein vereinfachtes Modell erwähnt: ein Lebenszyklus-Graph für einen altersklassifizierenden Lebenszyklus.

Die Übergangswahrscheinlichkeiten zwischen den Zuständen aus dem Modell können mit folgender zunächst allgemeiner Gleichung erfasst werden (S. 69):

(3)

{\vec {n}}(t+1)={\boldsymbol {A}}{\vec {n}}(t)

.

Hierbei stellt A die Populations-Projektions-Matrix dar und wird im Falle von altersklassifizierenden Lebenszyklus-Modellen auch als Leslie-Matrix bezeichnet. Der Vektor ${\vec {n}}(t)$ beschreibt die Zustandshäufigkeits-Verteilung und wird auch Populations-Vektor genannt. Der Zeitunterschied $t\rightarrow t+1$ wird hierbei als Projektionsintervall bezeichnet.

Entsprechend dem Lebenszyklus-Graphen aus Abb. 1 lassen sich die Elemente der Matrix A und die Elemente des Populations-Vektors ${\vec {n}}(t)$ wie folgt in die Gleichung (3) einfügen:

(4)

{\vec {n}}(t+1)={\begin{pmatrix}0&F_{2}&F_{3}\\P_{1}&0&0\\0&P_{2}&0\end{pmatrix}}{\begin{pmatrix}n_{1}\\n_{2}\\n_{3}\end{pmatrix}}(t)

.

Die Matrix A enthält die skalaren Elemente $F_{i}\geq 0$ für die Reproduktionswahrscheinlichkeiten (F von ‚fertility‘) und $P_{i}\geq 0$ für die Wahrscheinlichkeiten des Übergangs in den nächsten Zustand. Der Populations-Vektor ${\vec {n}}(t)$ enthält die Zustandshäufigkeits-Verteilung als Spalten-Vektor mit den skalaren Elementen $n_{i}$ für die gilt: $n_{i}\geq 0$ , und die im exemplarisch genannten Modell mit drei Zuständen bei Bedarf normiert sein können auf: $\textstyle \sum _{i=1}^{3}n_{i}=1.$

Nach Ausführung der Matrix-Multiplikation (Matrix mal Vektor) erhält man dann nach dem vorgesehenen ersten Projektionsintervall $t+1$ folgendes Ergebnis für den Populations-Vektor:

(5)

{\vec {n}}(t+1)={\begin{pmatrix}F_{2}\cdot n_{2}+F_{3}\cdot n_{3}\\P_{1}\cdot n_{1}\\P_{2}\cdot n_{2}\end{pmatrix}}(t+1)

.

Dieses zunächst formale Ergebnis kann man in der Abb. 1 verifizieren durch die jeweiligen Ergebnisse ‚am Ende der Pfeile‘: die Übergangswahrscheinlichkeit ( $F_{2},F_{3},P_{1},P_{2}$ ) multipliziert mit der zugehörigen Populationsgröße $n_{i}$ im jeweiligen Ausgangszustand 1, 2 oder 3. Durch Mehrfach-Ausführung eines solchen Projektionsschrittes, also eine Mehrfach-Ausführung der Matrix-Multiplikation und unter Verwendung konkreter Zahlenwerte, lässt sich nun die Entwicklung des Populations-Vektors ${\vec {n}}(t)$ über eine Vielzahl von Projektionsschritten im Rahmen des mathematischen Modells verfolgen bzw. voraussagen. Die Populations-Matrix A aus Gleichung (3) mit ihren Elementen kann hierbei im Modell konstant sein, sie kann aber auch variieren. Wenn sie variiert, dann kann sie von externen Faktoren z. B. dem Wetter, oder auch von internen Zuständen der Population selbst abhängen. Weiterhin können zufällige oder deterministische Effekte auftreten, und das Verhalten kann periodisch oder aperiodisch sein.

Lebenszyklus-Graph für einen größenklassifizierenden Lebenszyklus

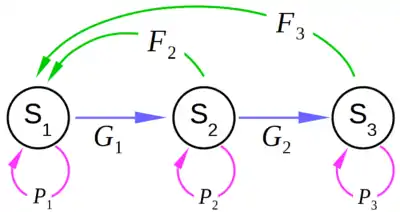
Abb. 2: Modell eines Lebenszyklus-Graphen für einen größenklassifizierenden Lebenszyklus mit drei Zuständen. Eingetragen sind die Übergangswahrscheinlichkeiten G in den jeweiligen Folgezustand, die Verweilwahrscheinlichkeiten P je Zustand, sowie die Reproduktionswahrscheinlichkeiten F.

Mit einem weiteren Modell lässt sich ein größenklassifizierender Lebenszyklus-Graph[8] mathematisch beschreiben. Abb. 2 zeigt einen solchen Graphen mit den Zuständen (states) S₁, S₂ und S₃. Diese Zustände beschreiben hier drei Größenklassen, wobei die Größe für den Folgezustand jeweils zunehmen soll. Ein Individuum kann von den Zuständen S₁ & S₂ in den jeweils nächsten Zustand gelangen mit der Wahrscheinlichkeit G_i und mit den Wahrscheinlichkeiten P_i auch im jeweiligen Zustand S₁, S₂ oder S₃ verweilen. Reproduktion wird durch die Wahrscheinlichkeiten F₂ und F₃ beschrieben und produziert neue Individuen im Zustand S₁. Sogenannte ‚absorbierende Zustände‘ sind in diesem Graphen nicht explizit eingezeichnet. Ein solcher absorbierender Zustand (Keyfitz/Caswell, S. 246, Zeilen 13–14)[7] liegt vor, sobald ein Individuum in einen Zustand kommt, diesen aber niemals mehr verlassen kann. Der Zustand S₃ wird beispielsweise zu einem absorbierenden Zustand, wenn gilt: F₃ = 0 und P₃ = 1.

Durch geeignetes Einfügen der Wahrscheinlichkeiten F₂, F₃, G₁, G₂, P₁, P₂ und P₃ aus Abb. 2 in die Populations-Projektions-Matrix A aus Gleichung (3) erhält man folgenden Populationsvektor für den Projektionsschritt $t+1$ :

(6)

{\vec {n}}(t+1)={\begin{pmatrix}P_{1}&F_{2}&F_{3}\\G_{1}&P_{2}&0\\0&G_{2}&P_{3}\end{pmatrix}}{\begin{pmatrix}n_{1}\\n_{2}\\n_{3}\end{pmatrix}}(t)

.

Nach Ausmultiplizieren der Matrix mal den Populations-Vektor erhält man für diesen ersten Projektionsschritt im Detail:

(7)

{\vec {n}}(t+1)={\begin{pmatrix}P_{1}\cdot n_{1}+F_{2}\cdot n_{2}+F_{3}\cdot n_{3}\\G_{1}\cdot n_{1}+P_{2}\cdot n_{2}\\G_{2}\cdot n_{2}+P_{3}\cdot n_{3}\end{pmatrix}}(t+1)

.

Ähnlich verhält sich dies für den zweiten Projektionsschritt, man erhält durch wiederholte Multiplikation mit der zugehörigen Populations-Projektions-Matrix A die folgende Gleichung:

(8)

{\vec {n}}(t+2)={\begin{pmatrix}P_{1}&F_{2}&F_{3}\\G_{1}&P_{2}&0\\0&G_{2}&P_{3}\end{pmatrix}}{\begin{pmatrix}P_{1}\cdot n_{1}+F_{2}\cdot n_{2}+F_{3}\cdot n_{3}\\G_{1}\cdot n_{1}+P_{2}\cdot n_{2}\\G_{2}\cdot n_{2}+P_{3}\cdot n_{3}\end{pmatrix}}(t+1)

und kann zum Ausmultiplizieren wiederum die Matrix-Multiplikation (Matrix mal Vektor) darauf anwenden.

Für den Fall von m diskreten Projektionsschritten unter Anwendung von Mehrfach-Multiplikationen der Matrix A für diese Projektionsschritte und unter Berücksichtigung der Klammersetzung bei Produkten (Assoziativität von Matrizen) lässt sich die Gleichung (3) wie folgt schreiben als:

(9)

{\vec {n}}(t+m)={\boldsymbol {A}}^{m}{\vec {n}}(t)

.

Hierbei bedeutet ${\boldsymbol {A}}^{m}$ eine Mehrfach-Multiplikation (Matrix mal Matrix für Blockmatrizen) der Matrix A mit sich selbst – unter Anwendung von genau m Matrix-Multiplikationen. Bereits bei P. H. Leslie (1945) findet man diese Art der Matrix-Potenzierung in der Form: ‚matrix M^t‘.[9]

Allgemein merkt die Quelle Keyfitz/Caswell an, dass ein Matrix-Modell eine große Menge an Informationen (‚contains a great deal of information‘, S. 245, Zeile 7)[7] über die Ereignisse, deren Wahrscheinlichkeiten, und über die zugehörigen Sequenzen beinhaltet.

Bei Bedarf lassen sich Markow-Ketten statt für diskrete Zeitschritte auch als mathematischer Markow-Prozess im kontinuierlichen Zeitbereich auswerten. Die Quelle ‚van Kampen‘ definiert dabei Markow-Ketten als Klasse von Markow-Prozessen,[10] wobei laut Quelle für Markow-Ketten insbesondere diskrete ganzzahlige[11] Zeitschritte gelten. Mit der etwas komplexeren sogenannten Mastergleichung[12] (Pauli-Mastergleichung oder ‚M-Equation‘[13]) lassen sich nun Markow-Prozesse im kontinuierlichen Zeitbereich auswerten.

Lebenszyklus-Graph für das Durchlaufen eines Ausbildungssystems

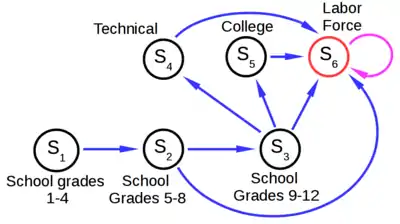
Abb. 3: Graph für das Durchlaufen eines Ausbildungssystems. Das Projektionsintervall beträgt hierbei 4 Jahre. Der rot markierte Zustand S₆ wird in diesem Modell als absorbierender Zustand behandelt.

Ein etwas komplexeres Modell wird nötig, um einen Graphen als Darstellung des Durchlaufens eines Ausbildungssystems bis zum Zustand der Erwerbstätigkeit mathematisch zu beschreiben. Die Klassifizierung der Ausbildungsstufen für das Modell aus Keyfitz/Caswell (S. 248) erfolgt hier jedoch etwas vereinfacht in nur fünf „Zuständen“ S₁ bis S₅. Die Einteilung in diesem noch recht allgemeinen System erfolgt in S₁: Schulklassen 1-4, S₂:Schulklassen 5-8, S₃: Schulklassen 9-12, S₄: Fachausbildung (‚Technical‘), S₅: Hochschule (‚College‘). Als abschließender Zustand in diesem Modell wird die Erwerbstätigkeit mit Zustand S₆ beschrieben. Dieser Zustand S₆ wird in diesem beschriebenen Modell als absorbierender Zustand erfasst, d. h. von diesem Zustand aus werden weitere Zustände nicht mehr erreicht, weder durch Reproduktion, noch durch Tod oder durch andere Übergänge. Der absorbierende Zustand S₆ ist damit auch kein Übergangszustand.

Zur mathematischen Beschreibung bietet es sich an, die Populations-Projektions-Matrix A aufzusplitten in:

(10)

{\boldsymbol {A}}={\boldsymbol {T}}+{\boldsymbol {F}}

mit den Dimensionen

\left({\begin{array}{c}s\times s\end{array}}\right)

je Einzelmatrix.

Hierbei beschreibt die Matrix T die Übergänge (ohne Reproduktion und ohne Wiederholungen), die Matrix F beschreibt die Reproduktionen, s ist die Zahl der Übergangszustände (states) im Modell ohne den absorbierenden Zustand S₆ und damit sowohl die Zahl der Zeilen als auch die Zahl der Spalten der jeweiligen Blockmatrix. Je nach Fokus der Untersuchungen im jeweiligen Modell lässt sich nun T (transition matrix) oder eher F (fertility matrix) genauer untersuchen. Im vorliegenden Fall des Modells aus Abb. 3 wird die Matrix T genauer untersucht. Bei fünf Übergangszuständen ist die Dimension dieser Matrix dann s = 5. Der in diesem Modell absorbierende Zustand S₆ (Erwerbstätigkeit) zählt hierbei separat. Die Übergangswahrscheinlichkeiten, die zu diesem Zustand S₆ führen, werden mit dem Zeilen-Vektor m erfasst und in Gleichung (11) genutzt, um die Matrix T auf die größere Matrix P zu erweitern. Reproduktionen werden hierbei, wie schon erwähnt, nicht abgebildet. Die Elemente der zugehörigen Matrix F sind in diesem Falle 0 und werden als Spalten-Vektor 0 in Gleichung (11) erfasst. Zur Beschreibung der Markow-Kette wird folgende verkürzte mathematische Darstellung für die Übergangsmatrix P genutzt:[14]

(11)

{\boldsymbol {P}}=\left({\begin{array}{c|c}{\boldsymbol {T}}&{\boldsymbol {0}}\\\hline {\boldsymbol {m}}&1\end{array}}\right)

mit den Dimensionen

\left({\begin{array}{c|c}s\times s&s\times 1\\\hline 1\times s&1\times 1\end{array}}\right)

unter Berücksichtigung von

{\text{Zeilenzahl}}\times {\text{Spaltenzahl}}

.

Die Zustände S₁ bis S₅ werden als ‚Übergänge‘ betrachtet, d. h. sie haben jeweils einen erreichbaren Folgezustand. Sie werden mit der Übergangsmatrix T erfasst. Die in dieser Formel (11) genutzte Darstellung $\left({\begin{array}{c|c}&\\\hline &\end{array}}\right)$ mit Markierungslinien zwischen den Einzelelementen der Matrix wird zur Kennzeichnung genutzt, um zu visualisieren, dass es sich hierbei um eine entsprechend zusammengesetzte Matrix handelt. Für den Zeilen-Vektor m ist zu berücksichtigen, dass die Gesamtsumme der Wahrscheinlichkeiten in Gleichung (11) je Spalte in der Matrix P genau 1 ergeben muss:

(12)

\sum _{i}{t_{ij}}+m_{j}=1

mit m_j als Elemente vom Zeilen-Vektor m und t_ij als Elemente von Matrix T.

Weiterhin gilt, analog zu Gleichung (3), für im jetzigen Fall einen Spalten-Vektor ${\vec {x}}(t)$ , der die Wahrscheinlichkeitsverteilung der Zustände aus Abb. 3 widerspiegeln soll, folgende Gleichung:[15]

(13)

{\vec {x}}(t+1)={\boldsymbol {P}}{\vec {x}}(t)

.

Zur Erstellung der Matrix P bzw. der Matrix T geht man nun wie folgt exemplarisch vor: Die Übergangswahrscheinlichkeit p₃₂ bei Spalte 2 und Zeile 3 für die unten folgende Gleichung (14) gilt für den Übergang von Zustand S₂ ‚alt‘ nach Zustant S₃ ‚neu‘ und ist laut Abb. 3 auch als Übergang vorgesehen. Ist für die zu prüfende Stelle in der Matrix kein Übergang im Lebenszyklus-Graph vorgesehen, so wird eine Null (‚0‘) an der zugehörigen Position der Matrix vermerkt. Alle Elemente der Matrix sind entsprechend zu prüfen. Aus dem Lebenszyklusgraphen aus Abb. 3 erhält man letztlich inklusive der Übergänge in den absorbierenden Zustand S₆ für die Übergangsmatrix P folgende Gleichung:

(14)

{\boldsymbol {P}}=\left({\begin{array}{ccccc|c}0&0&0&0&0&0\\1&0&0&0&0&0\\0&p_{32}&0&0&0&0\\0&0&p_{43}&0&0&0\\0&0&p_{53}&0&0&0\\\hline 0&1-p_{32}&1-p_{43}-p_{53}&1&1&1\end{array}}\right)

mit der Gesamt-Dimension

(s+1)\times (s+1)

.

Hieraus wird deutlich, dass die Übergangsmatrix P zwar für die Berechnung der Projektionsschritte $t\rightarrow t+1$ benötigt wird, aber die etwas kleinere Matrix T zur Erfassung der Wahrscheinlichkeitswerte der Übergänge der Markow-Kette genügt. Die Matrix P lässt sich dann aus T berechnen. Des Weiteren sieht man an diesem Beispiel, dass sich ‚Verzweigungen‘ in einem Lebenszyklus-Graphen, z. B. von Zustand S₃ nach S₄ bzw. nach S₅ in einfacher Weise mittels eines Matrix-Modells abbilden lassen.

Allgemein merkt Quelle (D. Schulz, 2010) zu Markow-Ketten an, dass sie ein einfaches und anschauliches Modell sind, um realweltliche Vorgänge mathematisch abzubilden.[16]

Forscher des Bundesinstituts für Bevölkerungsforschung (BiB, Deutschland) berichten, dass es bzgl. Kinderlosigkeit „erhebliche Unterschiede zwischen den Berufen gibt. 2009 war die Kinderlosigkeit bei Landwirtinnen und nicht erwerbstätigen Frauen (meist Hausfrauen) am geringsten.“.[17] Eine hohe Kinderlosigkeit findet man hingegen bei „Geschäftsführerinnen“, dort „lag der Anteil der kinderlosen Frauen bei 45 Prozent.“[17] Weitere Quellen berichten: „gebären Frauen mit Hochschulabschluss in Deutschland immer noch deutlich weniger Kinder als Frauen ohne Uniabschluss“ (Artikel von 2012)[18] und die „Zahl der Hochschulabsolventinnen ohne Nachwuchs steigt hierzulande weiter an“ (Deutschland, 2018).[19] Ähnlich werden Unterschiede der Kinderzahl pro Frau in Abhängigkeit von der Staatsangehörigkeit berichtet, z. B. „Bekommen Österreicherinnen durchschnittlich 1,27 Kinder in ihrem Leben, so sind es bei Ausländerinnen (Herkunft) 1,84 Kinder.“[20]

Eine sorgfältige Untersuchung unterschiedlicher Lebenswegentscheidungen mittels des mathematischen Modells der Markow-Ketten, ob die Ermittlung der genauen Verursacher und der Quellen der Ablenkung vom Familiengeschehen, mit einer folgenden sowohl ausreichend umfangreichen als auch rechtlich zulässigen Kompensation durch die Verursacher exakt an diesen ermittelten Stellen, zu einer Angleichung der unterschiedlichen Werte der Kinderzahl pro Frau z. B. bei unterschiedlichen Berufen,[17] bzw. unterschiedlicher Ausbildung[18][19] oder bei unterschiedlicher Staatsangehörigkeit[20] führen kann, ist in Quelle Keyfitz/Caswell bisher nicht auffindbar.

Siehe auch

Weblinks

MPIDR - Forschungsgruppe: Mathematische Demografie - demogr.mpg.de (Archiv-Version vom 31. Oktober 2020), abgerufen am 11. Juni 2021.
Karl-Peter Hadeler, Hans Heesterbeek: Mathematische Demographie und Epidemiologie (springer.com), abgerufen am 17. Dezember 2018.
Peter Drössler: Markov-Ketten in der Biologie (Anwendungen) - pe-home.de, Seite 3: Wright-Fischer-Modell (Statistik genbasierter biologischer Vielfalt in Populationen); Moran-Modell im Abschnitt 2.1 (Seite 9 von 10): „Entwicklung einer Bevölkerung in Form einer Geburten-Sterbe-Kette“, abgerufen am 15. Oktober 2020.

Einzelnachweise

Nathan Keyfitz, Hal Caswell: Applied Mathematical Demography., 3. Aufl. Springer Science+Business Media, 2005, ISBN 0-387-22537-4, S. 425f. (englisch)
R. E. Frisch: Weight at menarche: Similarity for well-nourished and undernourished girls at differing ages, and evidence for historical constancy. In: Pediatrice. Band 50, 1972, S. 445–450; Quellenangabe aus „Keyfitz/Caswell“ entnommen.
Nathan Keyfitz, Hal Caswell: Applied Mathematical Demography. 3. Auflage. Springer Science+Business Media, 2005, ISBN 0-387-22537-4, S. 504. (englisch)
Nathan Keyfitz, Wilhelm Flieger: World Population: An Analysis of Vital Data. The University Press, Chicago, Illinois, USA 1968, S. 659.
Schweiz Art 94 ZGB, A. Ehefähigkeit, zgb.gesetzestext.ch, abgerufen am 10. Januar 2018.
Österreich: ehemündig mit 16 J und darunter (minderjährig) auf Antrag, sonst 18 J, help.gv.at, abgerufen am 15. Januar 2018.
Nathan Keyfitz, Hal Caswell: Applied Mathematical Demography. 3. Auflage. Springer Science+Business Media, 2005, ISBN 0-387-22537-4, S. 245ff. (englisch)
Nathan Keyfitz, Hal Caswell: Applied Mathematical Demography. 3. Auflage. Springer Science+Business Media, 2005, ISBN 0-387-22537-4, S. 68f. (englisch)
P. H. Leslie: On the Use of Matrices in Certain Population Mathematics. In: Mathematical Demography. 2. Auflage. (selected papers), Springer, 2013, ISBN 978-3-642-35857-9, S. 215 (zehnte Zeile von oben).
N. G. van Kampen: Stochastic Processes in Physics and Chemistry. 2., überarb. Auflage. Elsevier Science Publishers, 1992, ISBN 0-444-89349-0, S. 89 (unten).
N. G. van Kampen: Stochastic Processes in Physics and Chemistry. 2., überarb. Auflage. Elsevier Science Publishers, 1992, ISBN 0-444-89349-0, S. 90 (oben).
N. G. van Kampen: Stochastic Processes in Physics and Chemistry. 2., überarb. Auflage. Elsevier Science Publishers, 1992, ISBN 0-444-89349-0, S. 97 (Gleichungen 1.4, 1.5 und 1.6)
N. G. van Kampen: Stochastic Processes in Physics and Chemistry. 2., überarb. Auflage. Elsevier Science Publishers, 1992, ISBN 0-444-89349-0, S. 98 (vierte Zeile von oben)
Nathan Keyfitz, Hal Caswell: Applied Mathematical Demography. 3. Auflage. Springer Science+Business Media, 2005, ISBN 0-387-22537-4, S. 246. (englisch)
Nathan Keyfitz, Hal Caswell: Applied Mathematical Demography. 3. Auflage. Springer Science+Business Media, 2005, ISBN 0-387-22537-4, S. 247. (englisch)
D. Schulz: Eine Einführung in zeit-diskrete Markov-Ketten. Forschungsarbeit. GRIN-Verlag, München 2010, ISBN 978-3-640-79708-0, S. 3 (oben).
Miriam Hollstein, 19. September 2012: Akademikerinnen bekommen mehr Kinder, im Abschnitt „Vor allem in Westdeutschland ein Problem“, welt.de, abgerufen am 5. Mai 2018.
focus.de, 20. September 2012: Deutschlands Geburtenrate sinkt schon wieder, im Abschnitt: „Akademikerinnen bekommen wieder mehr Kinder“, abgerufen am 5. Mai 2018.
Dorothea Siems, 7. März 2018: Der traurige Spitzenplatz deutscher Akademikerinnen, 1. Satz im Artikel (html), welt.de, abgerufen am 6. Mai 2018.
auslaender.at, 4. Januar 2012: Die Geburtenrate bei Ausländerinnen, im Abschnitt: „Die Geburtenrate in Österreich“, abgerufen am 5. Mai 2018.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Keyfitz_ApplMathDemography-1] Nathan Keyfitz, Hal Caswell: Applied Mathematical Demography., 3. Aufl. Springer Science+Business Media, 2005, ISBN 0-387-22537-4, S. 425f. (englisch)

[2] R. E. Frisch: Weight at menarche: Similarity for well-nourished and undernourished girls at differing ages, and evidence for historical constancy. In: Pediatrice. Band 50, 1972, S. 445–450; Quellenangabe aus „Keyfitz/Caswell“ entnommen.

[KeyfitzCaswell_b-3] Nathan Keyfitz, Hal Caswell: Applied Mathematical Demography. 3. Auflage. Springer Science+Business Media, 2005, ISBN 0-387-22537-4, S. 504. (englisch)

[4] Nathan Keyfitz, Wilhelm Flieger: World Population: An Analysis of Vital Data. The University Press, Chicago, Illinois, USA 1968, S. 659.

[5] Schweiz Art 94 ZGB, A. Ehefähigkeit, zgb.gesetzestext.ch, abgerufen am 10. Januar 2018.

[6] Österreich: ehemündig mit 16 J und darunter (minderjährig) auf Antrag, sonst 18 J, help.gv.at, abgerufen am 15. Januar 2018.

[KeyfitzCaswell_3rdEd_S245-7] Nathan Keyfitz, Hal Caswell: Applied Mathematical Demography. 3. Auflage. Springer Science+Business Media, 2005, ISBN 0-387-22537-4, S. 245ff. (englisch)

[KeyfitzCaswell_3rdEd_S68-8] Nathan Keyfitz, Hal Caswell: Applied Mathematical Demography. 3. Auflage. Springer Science+Business Media, 2005, ISBN 0-387-22537-4, S. 68f. (englisch)

[9] P. H. Leslie: On the Use of Matrices in Certain Population Mathematics. In: Mathematical Demography. 2. Auflage. (selected papers), Springer, 2013, ISBN 978-3-642-35857-9, S. 215 (zehnte Zeile von oben).

[10] N. G. van Kampen: Stochastic Processes in Physics and Chemistry. 2., überarb. Auflage. Elsevier Science Publishers, 1992, ISBN 0-444-89349-0, S. 89 (unten).

[11] N. G. van Kampen: Stochastic Processes in Physics and Chemistry. 2., überarb. Auflage. Elsevier Science Publishers, 1992, ISBN 0-444-89349-0, S. 90 (oben).

[12] N. G. van Kampen: Stochastic Processes in Physics and Chemistry. 2., überarb. Auflage. Elsevier Science Publishers, 1992, ISBN 0-444-89349-0, S. 97 (Gleichungen 1.4, 1.5 und 1.6)

[13] N. G. van Kampen: Stochastic Processes in Physics and Chemistry. 2., überarb. Auflage. Elsevier Science Publishers, 1992, ISBN 0-444-89349-0, S. 98 (vierte Zeile von oben)

[KeyfitzCaswell_3rdEd_S246-14] Nathan Keyfitz, Hal Caswell: Applied Mathematical Demography. 3. Auflage. Springer Science+Business Media, 2005, ISBN 0-387-22537-4, S. 246. (englisch)

[KeyfitzCaswell_3rdEd_S247-15] Nathan Keyfitz, Hal Caswell: Applied Mathematical Demography. 3. Auflage. Springer Science+Business Media, 2005, ISBN 0-387-22537-4, S. 247. (englisch)

[16] D. Schulz: Eine Einführung in zeit-diskrete Markov-Ketten. Forschungsarbeit. GRIN-Verlag, München 2010, ISBN 978-3-640-79708-0, S. 3 (oben).

[MiriamHollstein_2012-17] Miriam Hollstein, 19. September 2012: Akademikerinnen bekommen mehr Kinder, im Abschnitt „Vor allem in Westdeutschland ein Problem“, welt.de, abgerufen am 5. Mai 2018.

[FocusDe_2012-18] us.de, 20. September 2012: Deutschlands Geburtenrate sinkt schon wieder, im Abschnitt: „Akademikerinnen bekommen wieder mehr Kinder“, abgerufen am 5. Mai 2018.

[DorotheaSiems_2018-19] Dorothea Siems, 7. März 2018: Der traurige Spitzenplatz deutscher Akademikerinnen, 1. Satz im Artikel (html), welt.de, abgerufen am 6. Mai 2018.

[Geburtenrate_bei_Ausländerinnen_2018-20] uslaender.at, 4. Januar 2012: Die Geburtenrate bei Ausländerinnen, im Abschnitt: „Die Geburtenrate in Österreich“, abgerufen am 5. Mai 2018.