Marching Cubes
Marching Cubes ist ein Algorithmus zur Darstellung von Isoflächen in der 3D-Computergrafik. Er nähert eine Isofläche durch eine Polygongrafik an.
Entwicklung des Algorithmus
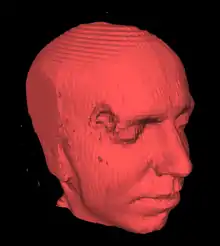
Marching Cubes wurde 1987 von William E. Lorensen und Harvey E. Cline als Ergebnis einer Forschungsarbeit für die Forschungsabteilung des Unternehmens General Electric in der Fachzeitschrift Computer Graphics vorgestellt. Lorensen und Cline beschäftigten sich mit der effizienten Visualisierung von Bilddaten bildgebender Verfahren wie Computertomografie, Magnetresonanztomografie und Single-Photon-Emissionscomputertomographie.[1][2]
Bedeutung des Algorithmus
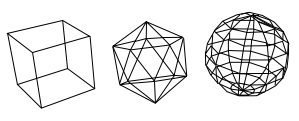
In der 3D-Computergrafik gibt es verschiedene Methoden, dreidimensionale Objekte zu modellieren. Eine davon ist die Modellierung als polygonale Oberfläche („Drahtgittermodell“): Man fügt eckige Flächen – in der Regel Dreiecke – so aneinander, dass sie die Oberfläche des Objektes nachbilden. Diese Modelle können sehr schnell und einfach in Bilder umgesetzt werden, der Speicherbedarf eines Modells ist relativ gering und durch zahlreiche Raffinessen sind sehr realistische Bilder möglich. Andererseits ist es fast unmöglich, auf diese Weise ein Medium wie Nebel zu modellieren, welches keine klar umrissene Oberfläche aufweist.
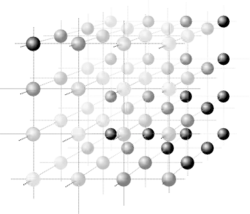
Eine andere Methode ist die Modellierung als Voxel-Datenmenge: In regelmäßigen Abständen wird an einem einzelnen Punkt aus dem Objekt die Dichte des Materials abgelesen; das Ergebnis ist ein würfelförmiges dreidimensionales Gitter aus Voxeln. Bildgebende Systeme wie die Computertomografie erzeugen von Natur aus solche Modelle. Diese Voxel-Modelle können recht einfach in Bilder umgesetzt werden, die zudem sehr realistisch und detailgetreu wirken. Allerdings benötigt das Modell sehr viel Speicherplatz – in Größenordnungen von mehreren hundert Megabyte bis einigen Gigabyte – und die Visualisierung dauert erheblich länger als bei einem polygonalen Oberflächenmodell vergleichbarer Größe. Zudem sind Manipulationen (zum Beispiel das Deformieren eines Objektes) deutlich schwieriger, teils sogar unmöglich.
Marching Cubes ermöglichte es erstmals, unpraktikable Volumen-Modelle durch praktikable polygonale Oberflächen-Modelle anzunähern, um sie anschließend effizient zu visualisieren. Der Algorithmus befriedigte damit den Wunsch der Radiologie nach einem Verfahren, Daten bildgebender Systeme wie der Computertomografie schnell und aussagekräftig bildlich darzustellen. Auch heute noch ist Marching Cubes als effizienter Transformationsalgorithmus im Einsatz. Zwar hat die Volumengrafik in der Zwischenzeit Fortschritte gemacht und durch 3D-Texturen Eingang in die Computergrafik-Praxis gefunden, jedoch gibt es bisher keine Hardware, welche die Volumengrafik auf ähnliche Weise beschleunigt, wie dies mit Grafikprozessoren für Dreiecke gelingt.
Der Algorithmus
Die Idee von Marching Cubes ist es, das gegebene Voxelmodell eines Objekts zunächst in kleine Würfel („cubes“) zu zerlegen und anschließend von einem Würfel zum nächsten zu „marschieren“ und zu bestimmen, wie die Oberfläche des Objekts den jeweiligen Würfel durchschneidet. Dazu wird ein vom Benutzer gewählter Grenzwert verwendet, um zu bestimmen, welche Teile der einzelnen Würfel innerhalb und welche außerhalb des letztendlichen Objekts liegen. Durch Veränderung dieses als „Dichte“ interpretierten Grenzwerts kann der Benutzer bestimmen, welche Bereiche des Objekts dargestellt werden und welche nicht.
Eingabe
Der Algorithmus verarbeitet folgende Eingabeparameter:
- Voxelgrafik. Das Volumen-Modell des Objekts.
- Format: Für gewöhnlich liegt eine Voxelgrafik als Liste L zweidimensionaler Arrays Ai - genannt „Scheiben“ – vor. Es gilt: L(i) = Ai, ferner ist Az[x,y] = ρx,y,z ∈ [0,1] der Dichtewert des modellierten Objektes an der Stelle (x,y,z).
- Dichtewert ρ . Über diesen Parameter wird gesteuert, welche Bereiche des Modells als solide und welche als transparent interpretiert werden.
- Format: ρ ∈ [0,1].
Datenstrukturen

Die folgenden Datenstrukturen werden vom Algorithmus verwendet oder erzeugt, aber nicht als Eingabeparameter übergeben:
- Triangle Lookup Table (TLT). Es gibt 256 Möglichkeiten, wie eine beliebig geformte Oberfläche einen Marching-Cubes-Würfel in Innen- und Außenbereiche aufteilen kann; denn laut Kombinatorik gibt es 28 = 256 Möglichkeiten, die 8 Ecken eines Marching-Cubes-Würfels in 2 Mengen „innerhalb“ und „außerhalb“ aufzuteilen. Die Triangle Lookup Table enthält alle diese Möglichkeiten; dabei gibt es aufgrund der Symmetrie der Fälle tatsächlich nur 15 voneinander verschiedene Einträge.
- Format: TLT(i) = v1, v2, v3, …, für den Fall i liefert TLT(i) eine Liste aller benötigten Dreiecke bestehend aus je drei Knoten.
- D. Der Algorithmus erstellt hier eine Liste aller Dreiecke, die benötigt werden, um die eingegebene Voxelgrafik durch eine Polygongrafik anzunähern.
- N. Zusätzlich zu der Dreiecksliste erstellt der Algorithmus hier eine Liste aller Einheitsnormalen der Knoten der Dreiecke.
Verarbeitung
- Daten einlesen. Der Algorithmus wählt zunächst zwei direkt aufeinanderfolgende Scheiben Ai und Ai+1 aus dem eingegebenen Voxelmodell aus.
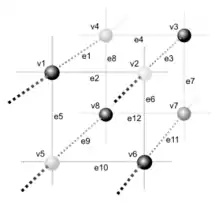
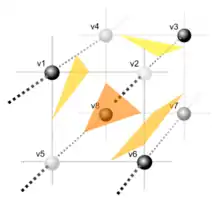
- Kubus bilden. Dann bildet der Algorithmus aus vier benachbarten, ein Quadrat bildenden Knoten der Scheibe Ai und den vier direkt gegenüberliegenden Knoten der Scheibe Ai+1 einen Kubus. Die acht Ecken des Kubus werden als v1, …, v8, die zwölf Kanten als e1, …, e12 durchnummeriert; v steht dabei für vertex, „Knoten“, e für edge, „Kante“ (siehe Abbildung).
- Index des Kubus berechnen. Nun wird aus den Voxelwerten der acht Knoten ein Index gebildet: Ist vi > ρ, so ist die i-te Ziffer eine 1, ansonsten eine 0. Man erhält also eine achtstellige Zahl, deren Ziffern jeweils 0 oder 1 sind, im Beispiel rechts 10100101. Betrachtet man dies als Binärzahl und wandelt sie in eine Dezimalzahl um, so erhält man den gewünschten Index i ∈ {0, 1, …, 255}.
- Benötigte Kanten erzeugen. Schlage den Eintrag i in der Triangle Lookup Table nach, also TLT(i). Erzeuge alle dort angegebenen Dreiecke.
- Oberflächenschnittpunkte interpolieren. Bestimme die Position jedes Knotens der eben erzeugten Dreiecke auf den Kanten des Würfels durch lineare Interpolation der anliegenden Ecken.
- Einheitsnormalen berechnen und interpolieren. Berechne für jede Ecke des Kubus die Einheitsnormale und interpoliere die Einheitsnormalen der Knoten der eben erzeugten Dreiecke durch lineare Interpolation zwischen den Einheitsnormalen der anliegenden Kubus-Ecken.
- Daten ausgeben. Füge die erzeugten Dreiecke und die dazugehörigen Einheitsnormalen der Liste aller bisher gefundenen Dreiecke und Einheitsnormalen hinzu und marschiere weiter zum nächsten Kubus.
Ausgabe
- D, die Liste aller erzeugten Dreiecksknoten.
- N, die Liste aller Einheitsnormalen in den Dreiecksknoten.
Funktionsweise
Der Standard-Algorithmus, wie ursprünglich von William E. Lorensen und Harvey E. Cline beschrieben, konstruiert eine facettierte Isofläche, indem er den Datensatz sequentiell würfelweise verarbeitet. Somit verarbeitet der Ansatz zuerst die m Würfel der ersten Zeile der ersten Schicht des Datensatzes in sequentieller Reihenfolge. Während dieser Verarbeitung wird jede Würfelecke, der einen Wert gleich oder über dem Isowert hat, markiert. Alle anderen Ecken bleiben unmarkiert. Die Isofläche schneidet jede Würfelkante, die mit einer markierten und einer unmarkierten Ecke endet. Jeder Würfel, der eine geschnittene Kante enthält, ist aktiv. Die Berechnungen, die die aktiven Würfel finden, können als die aktive Würfelbestimmungskomponente des Algorithmus angesehen werden. Diese Komponente kann als eigenständiger früher Verarbeitungsschritt implementiert oder in eine andere Verarbeitung integriert werden, aber in beiden Fällen beinhaltet sie das Durchlaufen von Datensätzen in sequentieller Reihenfolge.
Da jeder der 8 Eckpunkte eines Würfels entweder markiert oder unmarkiert sein kann, gibt es 28 = 256 mögliche Markierungsszenarien für einen Würfel. Der Standard-Algorithmus berücksichtigt jedoch Spiegelsymmetrie und Rotationssymmetrie, was zu nur 15 Markierungsszenarien führt. Spiegelsymmetrische Würfel haben das gleiche Würfel-Isoflächen-Schnittmuster. Zwei Würfel sind rotationssymmetrisch, wenn es eine Reihe von Drehungen gibt, die, wenn sie auf einen Würfel angewendet werden, ihn in eine neue Orientierung transformieren, in der die Markierung an jeder transformierten Ecke identisch mit der Markierung des anderen Würfels ist. Rotationssymmetrische Würfel haben äquivalente Würfel-Isoflächen-Schnittmuster. Die Schnittpunkte zwischen Isofläche und Kante können unter Verwendung einer Interpolationstechnik mit Subvertex-Genauigkeit geschätzt werden. Der Standard-Algorithmus verwendet lineare Interpolation, um den Schnittpunkt für jede Schnittkante zu schätzen. Wenn eine Kante mit der Einheitslänge die Endpunkte und hat, deren Skalarwerte bzw. sind, dann hat der Schnittpunkt bei einem Isowert Komponenten der Form:
wobei
Ein Vorteil der würfelweisen Verarbeitung des Standard-Algorithmus ist, dass jeder Kantenschnittpunkt nur einmal berechnet werden muss. Trotzdem können Algorithmen, die andere Durchlaufmuster verwenden, auch die gleichen Rechenvorteile durch die Verwendung von Zusatzdatenstrukturen, z. B. Hashtabellen, erreichen. Der letzte Schritt des Algorithmus besteht darin, dreieckige Facetten zu erzeugen, die den Teil der Isofläche darstellen, die jeden Würfel schneidet. Die Schnittpunkte definieren die Ecken der Dreiecke, und die Sammlung der dreieckigen Facetten in allen Würfeln bildet das dreieckige Netz, das die Isofläche definiert. Das Facettierungsmuster in jedem Würfel kann aus der Lookup-Tabelle für die Schnittpunkt-Topologie bestimmt werden. Die Verarbeitungsschritte, die die Facettierung aufbauen, können als Isoflächen-Komponente des Algorithmus betrachtet werden.[3]
Verbesserungen
Der oben dargestellte Algorithmus für Marching Cubes ist sehr rudimentär. Er nutzt beispielsweise nicht aus, dass bereits berechnete Informationen wieder verwendet werden können: Teilen sich zwei benachbarte Kuben eine Kante, so müssen darauf liegende Knoten nur einmal interpoliert werden; der Nachbar kann die bereits gefundenen Knoten einfach übernehmen.
Da die Laufzeit des Algorithmus nur von der Anzahl der betrachteten Kuben abhängig ist, liegt in der Verminderung dieser Anzahl das größte Einsparpotenzial. Weitere Optimierungsansätze versuchen daher, vor dem Marching Cubes-Durchlauf diejenigen Würfel aus der Datenmenge herauszufiltern, die ohnehin nicht mit der Isooberfläche in Berührung kommen. Dies sind diejenigen Kuben, die vollständig innerhalb oder vollständig außerhalb des Objektes liegen.
Octree
Eine 1992 von Wilhelms/van Gelder vorgeschlagene Methode besteht darin, das Volumen in einem Octree abzulegen. In einem Octree wird normalerweise jeder Würfel von Voxeln in acht Unterwürfel zerlegt. Zu jedem Würfel wird nun der niedrigste und der höchste Wert abgespeichert, der darin zu finden ist. Sind bei einem Würfel beide Werte gleich, so wird er nicht mehr weiter unterteilt. Das Ergebnis ist eine Hierarchie von kleiner werdenden Würfeln, für die jeweils ihr Werteintervall bekannt ist. Durch eine Traversierung dieser Hierarchie lassen sich nun diejenigen Würfel aussortieren, deren Minimum über oder deren Maximum unter dem Iso-Schwellwert liegt[4].
Das Verfahren hat die Nachteile, dass bei jeder Änderung des Isowertes die Hierarchie komplett neu durchlaufen werden muss und dass in realistischen Datensätzen, die normalerweise zentriert vorliegen, meist erst auf unteren Hierarchieebenen Würfel ignoriert werden können.
Approximation durch Diskretisierung
Hierbei handelt es sich um eine Vereinfachung des Marching Cube Algorithmus: die in der obigen Beschreibung des Algorithmus genannte Interpolation der Isoflächenschnittpunkte entfällt. Eckpunkte der durch den Algorithmus erzeugten Dreiecke sind dann lediglich die Mittelpunkte der zwölf Kanten des Würfels sowie sein Mittelpunkt. Auch die Flächennormalen müssen dann nicht mehr interpoliert werden, sondern können auch in einer Nachschlagetabelle gespeichert werden. Ein Vorteil dieser Approximation ist, dass nur noch Integer-Berechnungen durchgeführt werden müssen. Außerdem erhält man viele koplanare Dreiecksflächen, was die Anzahl der resultierenden Dreiecksflächen wesentlich reduziert.[5]
Softwarepatente
Der MC-Algorithmus ist ein Beispiel für die Auswirkungen von Softwarepatenten. Da der Algorithmus patentiert war, konnte er lange Jahre nicht verwendet werden, ohne Gebühren an den Entwickler zu zahlen. Daher wurde als Alternative der Marching Tetrahedrons entwickelt, welcher die Voxel-Würfel in Tetraeder unterteilte, und sonst gleich funktionierte. Das erteilte Patent US 4,710,876 wurde am 5. Juni 1985 angemeldet und galt in den Vereinigten Staaten 20 Jahre.[6]
Weblinks
Einzelnachweise
- William E. Lorensen, Harvey E. Cline: Marching Cubes: A high resolution 3D surface construction algorithm. In: Computer Graphics, Vol. 21, Nr. 4, Juli 1987, S. 163–169
- Timothy S. Newman, Hong Yi: A survey of the marching cubes algorithm In: Computer Graphics, Vol. 30, Nr. 5, Oktober 2006, S. 854–879
- Timothy S. Newman, Hong Yi: A survey of the marching cubes algorithm
- Jane Wilhelms, Allen van Gelder: Octrees for Faster Isosurface Generation. In: ACM Transactions on Graphics (TOG), Vol. 11, Nr. 3, S. 201–227, Juli 1992
- C. Montani, R. Scateni, R. Scopigno: Discretized Marching Cubes In: Visualization '94 Proceedings, IEEE Computer Society Press, 1994, S. 281–287
- System and method for the display of surface structures contained within the interior region of a solid body. Abgerufen am 20. Juni 2020 (englisch).