Französische Eisenbahnmetrik

In der Mathematik ist die Französische Eisenbahnmetrik ein ungewöhnliches Beispiel für eine Metrik.

Auf Paris zentrierte Hauptstrecken der Eisenbahn 1856

Es sei $X$ eine Menge von Punkten in der Ebene und $P$ ein fest gewählter Punkt.

Dann ist die französische Eisenbahnmetrik auf $X$ definiert durch die Funktion

d\colon X\times X\to \mathbb {R}

d(A,B)={\begin{cases}\|A-B\|&{\text{falls }}A,B{\text{ auf einer Geraden durch }}P{\text{ liegen, }}\\\|A-P\|+\|P-B\|&{\text{sonst}}.\end{cases}}

Die Konstruktion lässt sich ohne Schwierigkeiten auf beliebige euklidische oder unitäre Vektorräume verallgemeinern.

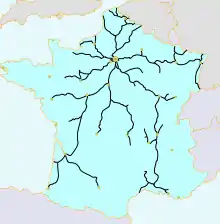
Der Name leitet sich von dem, insbesondere früher, sehr zentralisiert angelegten Eisenbahnnetz Frankreichs ab, bei dem fast alle Bahnverbindungen auf Paris zuliefen. Die Konsequenz davon war, dass man z. B. bei einer Bahnfahrt von Straßburg nach Lyon einen 400 km langen Umweg über Paris in Kauf nehmen musste, da keine direkte Verbindung existierte.

Eine Metrik ist die mathematische Verallgemeinerung der Distanz. Ist $X$ die Menge der französischen Städte mit Eisenbahnverbindung nach Paris ( $P$ ), dann kann in Analogie zur obigen Metrik die Fahrstrecke von Stadt $A$ zu Stadt $B$ sehr lang sein, wenn es keine direkte Verbindung, sondern nur eine Verbindung über $P$ gibt, auch wenn die Städte einander in Luftlinie nahe sind. Es ist ebenfalls der Name SNCF-Metrik gebräuchlich, nach der staatlichen französischen Eisenbahngesellschaft SNCF.

Eine andere durch spezielle Architektur motivierte Metrik ist die Manhattan-Metrik.

Literatur

Sur les groupes hyperboliques d'après Mikhael Gromov. (French) Papers from the Swiss Seminar on Hyperbolic Groups held in Bern, 1988. Edited by É. Ghys and P. de la Harpe. Progress in Mathematics, 83. Birkhäuser Boston, Inc., Boston, MA, 1990. ISBN 0-8176-3508-4

Weblinks

Plongement des espaces métriques et applications (Seite 5–6)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.