Luria-Delbrück-Experiment
Das Luria-Delbrück-Experiment (auch Fluktuationstest) ist ein von Salvador Edward Luria und Max Delbrück erdachtes und durchgeführtes Experiment, das 1943 publiziert wurde und das ein Teil der Arbeiten war, für die Luria und Delbrück 1969 zusammen mit Alfred Hershey mit dem Nobelpreis für Physiologie oder Medizin ausgezeichnet wurden.
Das Experiment, in dem die Resistenzbildung von Bakterien gegenüber Bakteriophagen untersucht wurde, zeigte, dass zufällige Mutationen in Bakterien spontan und damit auch in Abwesenheit von Selektionsmechanismen geschehen, und widerlegte die alternative Hypothese, dass diese als Reaktion auf geänderte Bedingungen in der Umwelt passieren. Mit Hilfe eines von Delbrück entwickelten mathematischen Modells ließen sich die Hypothesen auf quantitative Weise testen.
Außerdem konnten Luria und Delbrück mit Hilfe einiger Modellannahmen die Mutationsrate der Bakterien bestimmen. Zu diesem Zweck werden Fluktuationstests heute noch durchgeführt.
Ausgangssituation
Es war zur Zeit des Experiments schon länger bekannt, dass eine Bakterienkultur, die einem tödlichen Bakteriophagen ausgesetzt wird, durch diesen zunächst stark dezimiert wird. Nach einiger Zeit wächst die scheinbar eliminierte Kultur wieder heran, weil sich eine resistente Variante des Bakteriums gebildet hat, die sich ungehindert vermehren kann. Unbekannt war Anfang der 1940er jedoch der Mechanismus von Mutationen, insbesondere ob diese vor dem Hinzufügen des Virus oder als Reaktion hierauf erfolgen. Auch über die molekularen Grundlagen der Vererbung wusste man wenig, DNA als Träger der Erbinformation war noch nicht entdeckt.
Zu dieser Zeit führte Luria Experimente an Bakteriophagen durch. Eines seiner Probleme war hierbei, dass die Zahl gegen Phagen resistent gewordener Bakterien sehr großen Schwankungen unterworfen war. Die Idee zum Experiment kam Luria beim Betrachten eines Kollegen an einem Spielautomaten. Der Automat behielt für gewöhnlich den Einsatz des Spielers ein und schüttete dafür in seltenen Fällen den gesamten Jackpot aus. Luria erkannte, dass die Fluktuationen nicht als zu überwindendes Hindernis zu sehen waren, sondern selbst zum Gegenstand der Analyse gemacht werden sollten. Der gelernte Physiker Max Delbrück, dem Luria von seiner Idee berichtete, arbeitete hierauf die theoretischen Grundlagen des Experiments aus.[1]
Versuchsbeschreibung
Im Versuch wurde eine größere Anzahl von separaten Kulturen des Bakteriums Escherichia coli gebildet. Anfänglich vermehrten sich jeweils 50 bis 100 nichtresistente Bakterien in einer Nährlösung, bis Kolonien von etwa 109 Bakterien entstanden. Dann wurde jede der Kulturen auf Nährplatten einer hohen Konzentration von Bakteriophagen des für nichtresistente Bakterien tödlichen Typs T1 ausgesetzt. Nach einer Wartezeit von 24 und 48 Stunden wurden schließlich jeweils die Zahl der Kolonien (resistenter) Bakterien bestimmt und aus den Daten vieler Proben die resultierende Verteilung ermittelt.
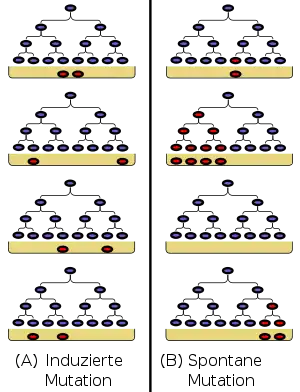
Das Hauptziel des Versuches bestand darin, zwischen zwei alternativen die Mutation betreffenden Hypothesen zu unterscheiden: Gemäß der ersten Hypothese erfolgt die Resistenzbildung in Bakterien als Reaktion auf den Angriff der Phagen. Mit einer geringen Wahrscheinlichkeit können einzelne Bakterien unabhängig voneinander eine Resistenz gegen die Phagen ausbilden, welche sie an ihre Nachkommen weitervererben. In diesem Fall entspricht die zu erwartende Verteilung der Kulturen einer Poisson-Verteilung. Deren Fluktuationen sind relativ gering, da die Varianz einer Poisson-Verteilung gleich ihrem Mittelwert ist. Würde diese Hypothese der „erworbenen Immunität“ zutreffen, sähen die Ergebnisse wie in der linken Spalte des Diagramms aus.
Gemäß der zweiten Hypothese geschehen resistenzbildende Mutationen andauernd mit einer kleinen Wahrscheinlichkeit, also auch bevor die Bakterienkultur von den Phagen angegriffen wurde. In den meisten Kulturen treten diese Mutationen spät auf, wenn die anfänglich 50 bis 100 Bakterien sich bereits stark vermehrt haben. Die resistenten Bakterien haben dann wenig Zeit, sich zu vermehren, und zum Zeitpunkt des Bakteriophagen-Angriffs sind nur wenige resistente Bakterien präsent, was zu geringen gemessenen Konzentrationen führt. In einigen wenigen Kulturen geschehen dagegen schon früh resistenzbildende Mutationen, so dass nach längerem exponentiellem Wachstum eine große Zahl Bakterien den Angriff der Phagen überlebt (siehe rechte Spalte des Diagramms). Hierdurch hat die gemessene Verteilung eine Varianz, die um ein Vielfaches größer ist als ihr Mittelwert. Es gibt seltene Ereignisse („Jackpot“), bei denen eine extrem große Anzahl von Bakterien gemessen wird. Ein von Delbrück entwickeltes mathematisches Modell erlaubte es, eine Formel für die Varianz der erwarteten Verteilung anzugeben und die Mutationsrate näherungsweise zu bestimmen.
Das Experiment bestätigte deutlich die Richtigkeit der zweiten Hypothese. Die gemessene Varianz der Verteilung war um ein Vielfaches größer als der Mittelwert und stimmte gut mit den Modellvorhersagen überein. Damit wurde die Existenz permanenter zufälliger Mutationen in Bakterien gezeigt.
Nachwirkung
Oft wurde der Fluktuationstest dahingehend interpretiert, dass er die Gültigkeit der darwinschen Evolutionstheorie in Bakterien zeige und lamarckistische Theorien widerlege. Luria selbst hatte die Bakteriologie als "letztes Bollwerk des Lamarckismus" bezeichnet.[2]
Luria und Delbrück selbst waren allerdings zunächst vorsichtig, was die Verallgemeinerbarkeit ihrer Ergebnisse angeht.[3] Ihre Ergebnisse wurden in den folgenden Jahren durch weitere Experimente bestätigt, in denen beispielsweise anstelle der Resistenz gegen Bakteriophagen die Resistenz gegen Penicillin oder Röntgenstrahlung getestet wurde.
Während Luria und Delbrück aus ihrem Modell nur Mittelwert und Varianz der nach der Theorie spontaner Mutationen zu erwartenden Verteilung berechneten, gelang es Lea und Coulson 1949, einen mathematischen Ausdruck für die Verteilung selbst herzuleiten.[4] Sie wird Luria-Delbrück-Verteilung genannt und wird auch heute noch zur Bestimmung von Mutationsraten verwendet.[5]
Ende der 1980er Jahre wurde die Allgemeingültigkeit der Zufälligkeit von Mutationen durch eine Arbeit von John Cairns und Mitarbeitern[6] in Frage gestellt. Cairns untersuchte im Gegensatz zu Luria und Delbrück Fälle nichtletaler Selektion (d. h. die Bakterien können unter Selektionsdruck überleben, sich aber nicht stark vermehren) und fand, dass für die Bakterien günstige Mutationen deutlich häufiger auftraten als es durch zufällige Mutationen zu erklären war. Nach einer längeren kontroversen wissenschaftlichen Debatte um dieses als Adaptive Mutation bezeichnete Phänomen ist heute bekannt, dass verschiedene Mechanismen existieren, durch die Organismen als Antwort auf äußeren Selektionsdruck die Häufigkeit von Mutationen erhöhen können, beispielsweise durch das Bilden von fehleranfälligen Polymerasen.[7] Die Existenz zielgerichteter Mutationen als Reaktion auf äußeren Selektionsdruck konnte jedoch nicht gezeigt werden.
Siehe auch
Literatur
- Luria, S. E., Delbrück, M.: Mutations of bacteria from virus sensitivity to virus resistance. In: Genetics. Band 28, Nummer 6, November 1943, S. 491–511, PMID 17247100, PMC 1209226 (freier Volltext).
Einzelnachweise
- E.P. Fischer: Max Delbrück. Genetics 177, 673–676 (2007)
- „Last stronghold of lamarckism“, G. Stent: The 1969 Nobel Prize for Physiology or Medicine. Science 24, 166 (1969)
- Luria, Delbrück, S. 509
- D. E. Lea, C. A. Coulson: The distribution of the number of mutants in bacterial populations J. Genet 49, 264–285 (1949)
- W. A. Rosche, P.L. Foster: Determining Mutation Rates in Bacterial Populations. Methods 20, 1 (2000)
- J. Cairns, J. Overbaugh S. Miller: The Origin of mutants, Nature 335, 142–145 (1988)
- S. M. Rosenberg: Evolving responsively: adaptive mutation, Nature Reviews Genetics 2, 504–515 (2001)