Luftlagerspindel
Eine Luftlagerspindel ist eine direkt angetriebene Welle mit einer Werkzeugschnittstelle, die durch ein Luftlager gelagert ist. Diese Spindeln finden vor allem Verwendung als Hauptspindel in Präzisions-Werkzeugmaschinen, bei der Mikrozerspanung und der Leiterplatten-Bohrindustrie. Durch die berührungslose Lagerung lassen sich sehr hohe Drehzahlen erreichen, was gerade in der Mikrozerspanung aufgrund der geringen Werkzeuggröße und der damit verbundenen hohen Schnittgeschwindigkeit wichtig ist.



Luftlager

In den nur wenige Mikrometer dicken Lagerspalten spielen dynamische Vorgänge wie Quetschfilmdämpfer, Scherströmungen (Dynamischer Auftrieb) und aerodynamische Effekte die dominierende Rolle und erzeugen Spaltströmungsgeschwindigkeiten (ohne irgendeine Bewegung der Lagerpaare) von mehr als 250 m/s.
Es werden aerodynamische sowie aerostatische Lager unterschieden, wobei der Lagerdruck bei ersterem lediglich durch die Relativbewegung der Lagerpaare selbst erzeugt wird, die hierfür besondere Merkmale wie Erhebungen und/oder Strukturen aufweisen. Die Abbildung zeigt als plakatives Beispiel eine Schnittdarstellung eines statischen sowie aerodynamischen Radiallagers ohne Welle. Bei aerostatischen Lagern muss der Lagerdruck von außen in den Lagerspalt eingebracht werden. Der Lagerspalt ist für statische Luftlager demnach abstrakt das dem Auslass und Einlass zwischenliegende Spaltsystem und ist von diesen in vielerlei Hinsicht und vor allem dynamisch abhängig.
Die Lagerfunktion basiert hierbei auf der axialen sowie tangentialen Druckverteilung, die Tragkraft generiert, als auch dem Luftdurchfluss durch den Lagerspalt, der hauptverantwortlich für die Generierung von Steifigkeit ist. Steifigkeit entspricht hier der Tragkraftänderung mit der radialen Verlagerung der Welle (Radiallager) oder der axialen Verlagerung der Platte (Axiallager). Die Druckverteilung als auch der Durchfluss jedoch sind Funktionen des Lagerspaltes sowie der Drosselung, wobei hier zwischen einer Drosselung am Eintritt (einlassgedrosselt) oder am Auslass (auslassgedrosselt) unterschieden wird.
Vorteile
Radiale Luftlagerungen können dieselben Steifigkeits- und gar bessere Dämpfungswerte als Wälzlagerungen erzielen sofern sie korrekt ausgelegt sind. Der nur wenige Mikrometer große Luftspalt eines Luftlagers jedoch besitzt durch die Eigenschaften der Luft einen Ausgleichseffekt gegenüber Form- und Größenfehlern der Welle oder des Lagers, der eine resultierende Genauigkeit erlaubt, die besser ist als die der Einzelkomponenten. Luftlagerspindeln besitzen eine um ca. Faktor zehn bessere Asynchrongenauigkeit gegenüber Wälzlagerspindeln und eine um ca. Faktor zwei bessere Synchrongenauigkeit. Somit können Steifigkeit und Dämpfung von Luftlagerungen mit denen von Wälzlagerungen durchaus konkurrieren, bieten aber radiale Fehlerbewegungen von teils weniger als 12 nm und axiale teils unter 10 nm, selbst bei Drehzahlen über 50.000/min und Relativgeschwindigkeiten von bis zu 250 m/s. Bei geringen Gleitgeschwindigkeiten sind Luftlagerungen zudem extrem reibungsarm und schmiermittelfrei, was ihren Einsatz bei zum Beispiel bei Navigationssystemen und in der Lebensmittelindustrie erklärt.
- kleinere Synchron- und entscheidend kleinere Asynchronfehler axial und radial
- Durch den Ausgleicheffekt des Mediums (Luft, z. B.) zwischen Lager und bewegter Welle werden Rotationsbewegungen erzeugt, die genauer sind als die Genauigkeiten der Summe der Einzelteile. Deshalb weisen Luftlagerspindeln im Vergleich zu Wälzlagern um einige Faktoren bessere Asynchron- und Synchronfehler auf, die Fehler von Lagerbahnen und allen Kugeln hart übertragen. Asynchronfehler von weniger als 10 nm sind bei langsam drehenden Spindelsystemen ohne Hürden möglich
- höhere Drehzahlen
- Neben kleineren Synchron- und Asynchronfehlern ist das charakteristischste Merkmal von Luftlagerspindeln die im Vergleich zum Wellendurchmesser von Wälzlagerspindeln erheblich höheren Drehzahlgrenzen. Schergeschwindigkeiten von 200 m/s in Radiallagern und 450 m/s in Axiallagern sind ohne Probleme zu realisieren.
- Höchstdrehzahl ohne zeitliche Begrenzung – zuverlässig stationärer Betrieb
- Wälzlagerspindeln können nicht im Dauerbetrieb auf Nenndrehzahl betrieben werden und antworten hierbei mit heiß werdenden Lagern, steigendem Laufgeräusch und letztendlichem Ausfall. Für die immer häufiger vorkommenden Applikationen mit Bearbeitungszeiten von Stunden bis Wochen bei höchsten Drehzahlen sind Luftlagerspindeln die perfekte Antwort, mit strikt konstanten Betriebsbedingungen und praktisch keinem Zeitlimit für den Dauerbetrieb bei Nenndrehzahl.
- extrem kurze Rampenzeiten
- Während bei Wälzlagerspindeln die Beschleunigungs- und Bremsrampenzeiten durch den Lagerkäfig begrenzt werden, begrenzt bei dynamisch gut ausgelegten Luftlagerspindeln lediglich der Maximalstrom des Motors die Beschleunigungs- und Bremswerte.
- keine Vorschmierzeit – unmittelbarer Betrieb
- Während Wälzlagerspindeln eine Vorschmierzeit von teils Minuten vor ihrem Betrieb und teils nach einer gewissen Betriebsdauer benötigen, ist eine Luftlagerspindel mit Anschalten von Lagerluft, Kühler und Umrichter direkt voll einsatzbereit.
- extrem kleines axiales Wellenwachstum über Drehzahl
- Benötigt das Wellenwachstum von teils 50–100 µm bei Wälzlagerspindeln eine Längenkompensation über die Maschinensteuerung, erlaubt eine richtig ausgelegte Luftlagerspindel mit 1–5 µm für die meisten Applikationen einen Verzicht auf eine solche.
- einfacher Aufbau und extrem kurze Reparaturzeiten
- Zwar ist eine Luftlagerspindel ähnlich belastbar wie eine Wälzlagerspindel, während jedoch Wälzlagerspindeln bei Überlast mit lauten Lagergeräuschen, höheren Lagertemperaturen und fehlenden Genauigkeiten antworten, blockieren meist die Wellen von Luftlagerspindeln.
- öl-, fett- und berührungsloser Betrieb
- Kein Fett, kein Öl, kein Verschleiß. Dies macht die Luftlagerspindel bei sachgerechter Behandlung prinzipiell wartungsfrei und erlaubt die Verwendung in gashaltiger und/oder reinraumähnlicher Umgebung oder zum Beispiel der Lebensmittelindustrie. Hier kann das umgebende Gas – z. B. CO2 – auch als Lagermedium verwendet werden.
- keine Anti-Statik Maßnahmen
- Die allgemein verbreitete Verwendung von Keramik-Wälzkörpern (Hybrid-Wälzlager) verlangt zur Vermeidung von Funkenbildung zwischen Werkzeug und Werkstück bei Wälzlagerspindeln Anti-Statik-Maßnahmen wie Bürsten oder Überschlagsdornen. Aufgrund der immensen Fläche zwischen Welle und Lager sowie dem nur wenige Mikrometer großen Spalten leiten Luftlagerspindeln über den sich ergebenden Kondensator diese Energien über die Lager und damit an den Schutzleiter weiter und machen die Verwendung von Anti-Statik-Maßnahmen generell überflüssig.
- kein axiales Rückhaltesystem beim Werkzeugwechsel
- Wälzlager verlangen ein äußerst kompliziertes Fangsystem, welches die axialen Kräfte beim Werkzeugwechsel aufnimmt, um die Spindellager nicht zu beschädigen. Der Axiallagerteller von Luftlagerspindeln jedoch ist derart groß, dass dieser sich beim Werkzeugwechsel einfach anlegt, bei äußerst kleinen Flächenpressungen.
Drosselung
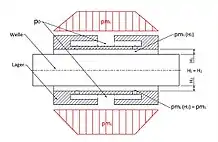

Am folgenden Beispiel (lagerinduzierte Eigenfrequenzmoden) soll erörtert werden, warum eine Drosselung des Zuführdrucks in den Lagerspalt eines statischen Luftlagers so wichtig und leistungsentscheidend ist. In der gezeigten Stabilitäts- und Resonanzanalyse ist die Welle zwischen oberem und unterem Lagerrand im geometrischen als auch physikalischen Gleichgewicht. Es herrscht rundum Druck pm=pm1=pm2 zwischen den Düsenreihen. Durch eine Störung – zum Beispiel Zerspankraft – verlagert sich die Welle nun gemäß Abbildung und erzeugt unterschiedlich große Spalte H1 und H2.
Würde der Zuführdruck P0 nun ungedrosselt in den Lagerspalt geleitet, würde über den Umfang überall der gleiche Druck und somit Kraft herrschen. Eine Rückstellkraft entgegen der "Störung" würde somit fehlen, das Lager hätte keine Funktion. Durch analytisch und iterativ berechnete und optimierte Düsen – gespeist durch den Zuführdruck p0 – wird ein Zwischendruck pm(H,p0...) nach der Düse erzeugt, der mitunter abhängig ist von der Lagerspaltdicke H unmittelbar nach der Düse. Ergo, je kleiner der Lagerspalt nach der jeweiligen Düse, desto höher der Zwischendruck pm,nach der Düse und damit auch die Druckkraft. Somit ist bei einer Verlagerung der Welle durch Störung eine wegabhängige Rückstellkraft und somit auch Steifigkeit – also Rückstellkraftänderung mit Verlagerung – gewährleistet.
Dynamik und Stabilität


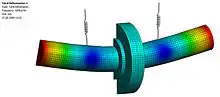
Ein statisches Luftlager besitzt eine externe Druckversorgung und generiert nach dem Prinzip der spaltabhängigen Drosselung Tragkraft, Steifigkeit und Dämpfung, wobei hierbei die Welle durch den Lagerspalt angekoppelt ist und mit ihren polaren und transversalen Trägheitsmomenten und ihrer Masse, abstrakt gesprochen, ein Feder-Masse-Dämpfer-System darstellt. Dementsprechend existieren demnach auch lagerinduzierte Eigenfrequenzen, sprich, stoße ich die Welle an, schwingt diese mit der lagerabhängigen Systemeigenfrequenz, wobei die Amplitude wiederum durch die Dämpfung bestimmt wird. Das impliziert auch, dass zum Beispiel ein luftgelagertes Spindelsystem von Natur aus ein schwingungsfähiges System mit den Moden „zylindrisch“ und „konisch“ darstellt, wobei der Drehpunkt des konischen Modus stets durch den Massenmittelpunkt der Welle geht. Diese Eigenfrequenzen jedoch hängen von den Lagersteifigkeiten ab, die wiederum sowohl von der Lagerspaltweite bzw. -form als auch von aerodynamischen Effekten bei Drehzahl abhängt. Somit verändert eine Spindel mit Drehzahl ihre Steifigkeit und somit auch die lagerinduzierten Eigenfrequenzen. Diese Eigenfrequenzen müssen aus zwei Gründen bekannt sein, zum einen, um Drehfrequenzen der Spindel in der Nähe dieser Eigenfrequenzen aufgrund von Vibrationen (Überhöhung) zu vermeiden, und um eine Stabilitätsanalyse anfertigen zu können.
Halbfrequenzwirbel
Hier ergibt sich nun ein sehr entscheidender Unterschied zu Wälzlagerungen, denn bei Luftlagern, sei es statischer oder dynamischer Natur, existiert der Zustand des Halbfrequenzwirbels, der unbedingt zu vermeiden und somit im Vorfeld zu berechnen ist. Der Halbfrequenzwirbel ist eine Instabilität von Luftlagern, bei der die Welle anfängt, mit halber Drehfrequenz gegen die Drehrichtung zu rühren. Dieser Zustand stellt sich ein, erreicht die Drehfrequenz und somit die drehfrequente Anregung mit der Unwucht das Doppelte der momentan herrschenden ersten Systemeigenfrequenz. Physikalisch gesehen ist dies der Zustand, bei dem die Dämpfung Null wird und die Amplituden somit unendlich.
Neben den lagerinduzierten starrkritischen Eigenfrequenzen existiert noch die biegekritische Eigenfrequenz der Welle selbst. Jedes Material besitzt einen E-Modul, der bildlich gesprochen einer Federrate entspricht. Somit ist – vergleichbar mit einer Stimmgabel – auch die Welle ein schwingungsfähiges System. Erreicht man mit der Drehfrequenz die Frequenz der biegekritischen Eigenfrequenz, fängt die Welle derart an zu schwingen, dass Luftlager aufgrund der engen Lagerspalte und geringen Dämpfung als auch Kugellagerlösungen hier versagen. Fluidlager jedoch besitzen genügend Dämpfung und genügend große Lagerspalte, um diese biegekritische Eigenfrequenz zu durchfahren. Eine luftgelagerte Welle wird somit hinreichend unterhalb der konischen/zylindrischen Starrkritischen, aber notwendigerweise unter der Halbfrequenzkritischen und der ersten Biegekritischen betrieben. Fluidgelagerte Spindeln oder Anlagen können jedoch durchaus zwischen der ersten und zweiten Biegekritischen betrieben werden.
Literatur
- J. Engmann: Galvanisch gebundene Mikroschleifstifte – Entwicklung, Herstellung und Einsatz. Dissertation: Technische Universität Kaiserslautern, Maschinenbau und Verfahrenstechnik, 2011, ISBN 978-3-941438-59-0
- R. Dupont: Isotrop und fliehkraftinvariant gestaltetes, gasgeschmiertes Spiralrillenlager in Kegelbauform für höchste Drehfrequenzen. Dissertation : Technische Universität Kaiserslautern, Maschinenbau und Verfahrenstechnik, 2005