Liniengleichnis
Das Liniengleichnis ist ein bekanntes Gleichnis der antiken Philosophie. Es stammt von dem griechischen Philosophen Platon (428/427–348/347 v. Chr.), der es am Ende des sechsten Buches seines Dialogs Politeia von seinem Lehrer Sokrates erzählen lässt. Unmittelbar zuvor hat Sokrates das Sonnengleichnis vorgetragen. Am Anfang des siebten Buches folgt das Höhlengleichnis, das letzte der drei berühmten Gleichnisse in der Politeia. Alle drei Gleichnisse veranschaulichen Aussagen von Platons Ontologie und Erkenntnistheorie.
In den drei Gleichnissen wird spezifisch platonisches Gedankengut vorgetragen. Der „platonische“ Sokrates, der hier als Sprecher auftritt und die Gleichnisse erzählt, ist eine literarisch gestaltete Figur. Seine Position kann daher nicht mit der des historischen Sokrates gleichgesetzt werden.
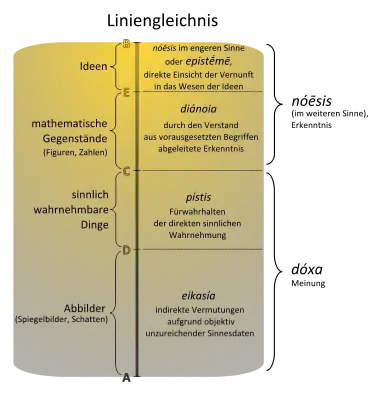
Im Liniengleichnis wird die gesamte erkennbare Wirklichkeit mit einer senkrecht vorgestellten Linie verglichen. Die Linie ist in vier ungleiche Abschnitte geteilt, die für vier Erkenntnisweisen und die diesen zugeordneten Erkenntnisgegenstände stehen. Zwischen ihnen besteht eine hierarchische Ordnung. Die Erkenntnisweisen sind nach ihrer Zuverlässigkeit, die Erkenntnisgegenstände nach ihrem Rang geordnet. Den zwei Hauptabschnitten der Linie entsprechen die Bereiche des sinnlich Wahrnehmbaren (unten) und des rein Geistigen (oben).
Inhalt
Im sechsten Buch der Politeia erläutert Sokrates seinen Gesprächspartnern Glaukon und Adeimantos, den beiden Brüdern Platons, die ethischen und intellektuellen Anforderungen, denen man genügen muss, um für das philosophische Studium des höchsten Erkenntnisbereichs und zugleich für politische Führungsaufgaben qualifiziert zu sein. Wer die erforderlichen Voraussetzungen erfüllt, hat sich um die Erkenntnis des „Guten“ zu bemühen, denn das Gute ist das höchstrangige Erkenntnisobjekt und letztlich das Ziel aller philosophischen Bestrebungen. In der platonischen Ideenlehre ist die Idee des Guten das oberste Prinzip. Sie ist aber wegen ihrer Transzendenz schwer zu erfassen. Im Sonnengleichnis hat Sokrates das Gute mit der Sonne verglichen: Wie im Bereich des Sichtbaren die Sonne als Quelle des Lichts die alles beherrschende Macht ist, so herrscht in der intelligiblen (geistigen) Welt das Gute als Quelle von Wahrheit und Wissen. Glaukon bittet um weitere Erläuterung, worauf Sokrates mit der Darstellung des Liniengleichnisses beginnt.[1]
Den Ausgangspunkt bildet die bereits im Sonnengleichnis veranschaulichte Teilung der Gesamtwirklichkeit in zwei analog strukturierte Bereiche, den sichtbaren (der Sinneswahrnehmung zugänglichen) und den geistigen (nur dem Erkenntnisbemühen zugänglichen). Glaukon soll sich eine senkrechte[2] Linie vorstellen, die in zwei ungleiche Hauptabschnitte geteilt ist. Die Hauptabschnitte stehen für die beiden Wirklichkeitsbereiche. Die ganze Linie wird in der Forschungsliteratur gewöhnlich mit AB bezeichnet, wobei A der untere, B der obere Endpunkt ist; der Punkt C teilt die Linie in die beiden Hauptabschnitte AC (unten, Sinneswelt) und CB (oben, geistige Welt). Jeder der beiden Hauptabschnitte ist im selben Verhältnis wie die ganze Linie unterteilt. So kommen vier Abschnitte zustande, zwei für die Sinneswelt (AD und DC) und zwei für die geistige Welt (CE und EB). Es ergibt sich die Proportion AC : CB = AD : DC = CE : EB.[3]
Das System ist so strukturiert, dass vom untersten Abschnitt der Linie zum obersten die Deutlichkeit, mit der die jeweiligen Objekte erfasst werden können, zunimmt. Dem entspricht eine Zunahme des objektiven Wahrheitsgehalts der jeweils erreichbaren Erkenntnisse und der Gewissheit, die der Erkennende erlangt. Die unterschiedlichen Erkenntnisweisen, die den Abschnitten der Linie entsprechen, sind durch die Qualität der Objekte bestimmt.
Erster Hauptabschnitt der Linie
Dem ersten Hauptabschnitt (AC) entspricht die Welt der sinnlich wahrnehmbaren Dinge. Seinen beiden Unterabschnitten sind unterschiedliche Arten von Objekten der Sinneswahrnehmung zugeordnet. Die Wahrnehmungsobjekte sind durch ihre Unbeständigkeit charakterisiert.
Der erste Unterabschnitt (AD) ist die Welt der undeutlichen Bilder, welche die Natur selbst erzeugt: Schatten sowie Spiegelbilder auf Wasseroberflächen und auf glatten und glänzenden Flächen. Der zweite Unterabschnitt (DC) ist die Welt der realen Dinge, der Körper, deren Abbildungen im ersten Unterabschnitt erscheinen. Hier sind wirkliche Tiere, Pflanzen und Gegenstände, die direkt angeschaut werden, wobei sich weit klarere, eindeutigere Sinneseindrücke ergeben als bei der Betrachtung der Schatten und Spiegelbilder.[4]
Unter erkenntnistheoretischem Gesichtspunkt entspricht der erste Hauptabschnitt dem Meinen (dóxa), den möglicherweise richtigen, aber nicht ausreichend begründeten Auffassungen. Das Meinen kommt in zwei Formen vor: Mutmaßen (eikasía), das dem Unterabschnitt AD zugeordnet ist, und Fürwahrhalten (pístis), das dem Unterabschnitt DC entspricht.
Die Eikasia als unterste Erkenntnisweise richtet sich auf die Schatten und Spiegelbilder, auf Objekte, deren Wahrnehmung nur Vermutungen ermöglicht, da die Gegenstände, die einen Schatten werfen bzw. sich spiegeln, außerhalb des Blickfelds sind. Aus dem Text geht nicht hervor, ob Platon hier unterstellt, dass sich der Vermutende der Abbildhaftigkeit des von ihm Wahrgenommenen nicht bewusst ist, sondern dieses für die ganze Realität hält,[5] oder ob gemeint ist, dass der Vermutende den Schatten und Spiegelbildern Informationen über deren Ursachen, die dreidimensionalen Objekte, entnimmt. Ein Beispiel für Letzteres wäre ein bewegter Schatten, der die Anwesenheit eines nicht sichtbaren Menschen oder Tieres anzeigt.[6]
Die Pistis als „Fürwahrhalten“ ist das Vertrauen in die Sinneswelt und die Richtigkeit der von den Sinnesorganen gelieferten Informationen. Sie basiert auf einer unmittelbaren Wahrnehmung realer dreidimensionaler Objekte, so wie diese sich den Sinnen darbieten. Daher ist ihr Wert höher als derjenige der Eikasia, denn hier können Kenntnisse erlangt werden, deren Wahrheitsgehalt größer ist.[7]
Zweiter Hauptabschnitt der Linie
Der zweite Hauptabschnitt (CB) stellt die geistige Welt dar. Seine Unterteilung in die beiden Unterabschnitte CE und EB ist der des ersten Hauptabschnitts analog. Im geistigen Bereich sind alle Erkenntnisobjekte vollkommen und absolut unveränderlich. Dadurch unterscheidet er sich fundamental von der Sinneswelt, dem Bereich des Werdens, in dem alles im Wandel begriffen ist.
Das begriffliche Denken der Mathematiker (diánoia)
Die Erkenntnisweise des begrifflichen Denkens (Dianoia) entspricht dem ersten Unterabschnitt (CE). Als ihre Objekte werden die Gegenstände der Mathematik genannt, vor allem ideale geometrische Figuren. Die durch Dianoia erreichbare Einsicht bedarf der Begründung durch Beweis. Sie führt zur Verstandesgewissheit und ist Voraussetzung dafür, dass man zu den Ideen als Grundprinzipien gelangt.
Die Mathematiker setzen ihre Begriffe (wie geometrische Figuren oder Winkelarten) als bekannt voraus und legen sie ihren Beweisgängen zugrunde, als wüssten sie darüber Bescheid. Sie klären ihre Begriffe aber nicht auf und sind außerstande, sich und anderen darüber Rechenschaft zu geben, was die damit bezeichneten Dinge in Wirklichkeit sind. Da sie ihre Voraussetzungen nicht prüfen, gehen sie nicht auf den „Anfang“ (ein Prinzip) zurück und erlangen über ihn kein Wissen; ihre Ausgangspunkte sind nur Annahmen, von denen sie zu Folgerungen fortschreiten.
Außerdem verwenden die Mathematiker sichtbare Abbildungen der Objekte, über die sie nachdenken. Sie zeichnen, obwohl die Gegenstände ihrer Bemühungen sinnlicher Wahrnehmung gänzlich entzogen sind; sie schauen auf die sichtbaren geometrischen Gestalten, denken aber an die Ideen, die von diesen Gestalten unzulänglich repräsentiert werden. Beispielsweise zeichnen sie eine Diagonale als sichtbare Linie, womit sie einen Bezug zur vertrauten Erfahrungswelt herstellen, obwohl die ideale Diagonale, um die es ihnen geht, unanschaulich ist. Sie kennen die Dinge, von denen die Mathematik handelt, nicht, denn sie haben es nur mit Abbildern dieser Dinge zu tun. Somit ist ihre Vorgehensweise der eigentlichen Natur dessen, womit sie sich befassen, nicht angemessen.[8] Sie stützen sich rechtfertigungslos auf angebliche Evidenz, auf nicht hinterfragte Annahmen. Das begriffliche Denken der Mathematiker zählt also nicht zur Vernunfteinsicht, sondern steht als Mittelding zwischen ihr und der bloßen Meinung, die bei der Auswertung von Sinneseindrücken zustande kommt. Der mathematische Gegenstandsbereich ist zwar geistig und daher grundsätzlich dem Wissen zugänglich, doch besitzen die Mathematiker kein wirkliches Wissen über ihn.[9]
Mit diesen Feststellungen will Platon nicht die zeitgenössischen Mathematiker kritisieren, insoweit sie als solche arbeiten, sondern nur aus philosophischer Sicht die Grenzen dessen aufzeigen, was Mathematik im Rahmen ihrer Möglichkeiten für die Wirklichkeitserkenntnis leisten kann.[10]
Die Vernunfteinsicht (nóēsis)
Platon weist die Noesis (Vernunfteinsicht), die höchste Erkenntnisweise, dem obersten Linienabschnitt (EB) zu.[11] An anderer Stelle verwendet er allerdings den Begriff Noesis in einem weiteren Sinne für die Gesamtheit der Erkenntnis geistiger Objekte, also für den ganzen oberen Hauptabschnitt der Linie, und nennt das Erkenntnisprodukt des obersten Unterabschnitts (EB) „Wissen“ (epistḗmē).[12] In der Forschungsliteratur wird „Noesis“ gewöhnlich im engeren Sinne aufgefasst und nur auf den obersten Unterabschnitt der Linie bezogen.
Die Noesis (im engeren Sinne) benötigt im Unterschied zur Dianoia keine Hilfsmittel aus der sinnlichen Anschauung, sondern findet ausschließlich innerhalb des rein geistigen Bereichs statt und erreicht den voraussetzungslosen wirklichen Anfang, den sie dann zum Fundament macht. So gewinnt sie einen festen Stand. Diese Vorgehensweise bezeichnet Platon als „dialektisch“. Unter Dialektik versteht er kein bestimmtes Sachwissen, keine Wissenschaft neben anderen Wissenschaften, sondern die Untersuchungsmethode der Philosophie, die aus seiner Sicht allein den Kriterien der Wissenschaftlichkeit genügt. Der Dialektiker ist in der Lage, methodische und andere Defizite der Mathematik zu erkennen und korrekte Aussagen über den Status mathematischer Gegenstände zu machen.[13] Die Aufgabe der Dialektik ist es, die objektiven Begriffsgehalte, die Ideen, in ihrem Wesen und Gesamtzusammenhang zu erfassen.
Die Noesis geht zwar wie die Dianoia zunächst von Voraussetzungen aus, steigt aber dann von dieser Ausgangsbasis aus zum Voraussetzungslosen auf, das keiner Begründung bedarf. Ist diese höchste Ebene erreicht, so werden die anfänglichen Voraussetzungen überflüssig. Das Voraussetzungslose wird dann seinerseits zum Ausgangspunkt für die – nunmehr korrekt fundierte – Erkenntnis aller ihm untergeordneten Wissensbereiche, der Gesamtheit des Wissbaren. Auf den Aufstieg zur höchsten Ebene des Erkennbaren folgt somit ein Abstieg.[14]
Das Voraussetzungslose, das Voraussetzung für alles andere ist und von dem alles andere abgeleitet wird, ist das höchste Prinzip, das im Sonnengleichnis mit der Idee des Guten gleichgesetzt wurde.[15] Damit kehrt die Erörterung zu ihrem Ausgangspunkt zurück: Das Liniengleichnis dient der Erläuterung des Sonnengleichnisses. Mit dem anschließend dargelegten Höhlengleichnis soll der Gedankengang weiter vertieft werden.
Platon vertritt somit das Konzept einer Universalwissenschaft, die alle Forschungszweige in einem einzigen Prinzip verankert und so zusammenfasst. Diese Universalwissenschaft soll so verschiedene Gebiete wie Mathematik und Ethik auf eine gemeinsame Wurzel zurückführen und dadurch vereinigen. Den Hintergrund bildet die Ideenlehre: Die Gegenstände der Mathematik sind ebenso wie die der Ethik Ideen und als solche ontologisch von der höchsten Idee, der Idee des Guten, abhängig.[16]
Rezeption
Antike und Frühe Neuzeit
Im Mittelplatonismus fand das Liniengleichnis relativ wenig Beachtung. Plutarch fasste den Inhalt knapp zusammen und erörterte die Frage, wieso die Abschnitte der Linie ungleich sind und welcher der beiden Hauptabschnitte der größere ist (hierzu fehlen im Gleichnis Angaben).[17] Alkinoos ging in seinem Didaskalikos, einer Einführung in die platonische Philosophie, darauf ein.[18]
Wesentlich intensiver war die Rezeption des Gleichnisses bei den spätantiken Neuplatonikern. Iamblichos interpretierte es in seiner Schrift „Die Wissenschaft der Mathematik im allgemeinen“ (De communi mathematica scientia), Calcidius gab es in seinem Kommentar zu Platons Dialog Timaios ausführlich wieder, Syrianos und Proklos behandelten es in ihren Kommentaren zur Politeia und Asklepios von Tralleis erläuterte es in seinem Kommentar zur Metaphysik des Aristoteles.[19]
Im 16. Jahrhundert zog der Philosoph Francesco Patrizi das Liniengleichnis im Rahmen seiner Aristoteleskritik heran. Er versuchte die Überlegenheit der platonischen Philosophie über die aristotelische nachzuweisen und erläuterte dabei anhand von Zitaten aus dem Liniengleichnis sein Verständnis der analytischen Methode Platons, die Aristoteles ignoriert habe.[20]
Moderne Forschung
Im 19. Jahrhundert wurde die Deutung des Gleichnisses in der Platonforschung meist als relativ unproblematisch betrachtet. Eine intensive Debatte begann erst in den 1920er-Jahren.
Eine Forschungsdiskussion betrifft die Frage, ob der erste Hauptabschnitt der Linie einen realen, kontinuierlichen Erkenntnisgewinn beim Voranschreiten von unten nach oben ausdrückt, also eine eigenständige Funktion hat, oder ob er nur der vorbereitenden Illustration des im zweiten Hauptabschnitt Dargelegten dient.[21]
Seit langem umstritten ist die Frage, ob die vier Abschnitte der Linie und die ihnen zugeordneten Erkenntnisarten den Aufstiegsphasen im Höhlengleichnis entsprechen. Eine Übereinstimmung gilt vielen Forschern als plausibel, aber manche sehen keine Analogie zwischen der Höhle und dem unteren Teil der Linie.[22]
Eine weitere Unklarheit betrifft den Status der Gegenstände der Mathematik. Einer Hypothese zufolge haben sie gegenüber den Ideen einen eigenen ontologischen Status und daher ist ihnen auf der Linie ein eigener Abschnitt zugewiesen, die Ideenerkenntnis bleibt dem obersten Abschnitt vorbehalten.[23] Nach einer anderen Forschungsmeinung geht es im gesamten oberen Hauptabschnitt der Linie um Ideenerkenntnis; Dianoia und Noesis sind nur zwei unterschiedliche Zugangsweisen zur Ideenwelt.[24]
Aufgrund der Proportionalität (AC : CB = AD : DC = CE : EB) müssen die beiden mittleren Unterabschnitte der Linie gleich lang sein. Dieser Umstand wird aber in der Darstellung des Gleichnisses nicht erwähnt. Umstritten ist, ob es sich dabei um einen Zufall handelt oder ob sich dahinter eine Bedeutung verbirgt.[25]
Nach einer von manchen Forschern vertretenen Interpretation des Liniengleichnisses handelt es sich nicht um vier Erkenntnisweisen, sondern nur um drei: wahrnehmende, mathematische und dialektische Erkenntnis.[26] Zu den Befürwortern dieser Deutung gehört Theodor Ebert. Er meint, die Erkenntnisweisen seien miteinander verkettet und nicht, wie die irrige Vorstellung von Erkenntnis- und Wirklichkeitsstufen besage, aufgrund einer ontologischen Differenz ihrer Gegenstände voneinander geschieden. Die Unterscheidung von Urbild und Abbild sei funktional, nicht ontologisch zu verstehen. Die Annahme, das Liniengleichnis illustriere Erkenntnis- und Wirklichkeitsstufen, gehe auf ein Missverständnis des Aristoteles zurück, dem sich die späteren Platoniker diesbezüglich angeschlossen hätten. Nach der Überzeugung von Ebert und manchen anderen Philosophiehistorikern vertrat Platon keine dualistische Metaphysik mit ontologischer Trennung (Chorismos) zwischen intelligibler und sinnlich wahrnehmbarer Welt.[27] Die traditionelle, gängige Gegenauffassung, die auch weiterhin in der Forschung dominiert, geht von zwei ontologisch verschiedenartigen Bereichen oder „Welten“ aus. Die ontologische Verschiedenheit betonen u. a. Rafael Ferber, der die Bezeichnung „Zwei-Welten-Theorie“ verwendet, Michael Erler, der Platons Ontologie ebenfalls als „Zweiweltenlehre“ charakterisiert und dazu bemerkt, Aristoteles spreche „nicht ohne Grund von einem Chorismos“, sowie Thomas Alexander Szlezák.[28]
Wolfgang M. Ueding hat versucht, das Liniengleichnis als ein musikalisches Diagramm zu rekonstruieren.[29]
Textausgaben und Übersetzungen
- Otto Apelt, Karl Bormann: Platon: Der Staat. Über das Gerechte (= Philosophische Bibliothek, Bd. 80). 11., durchgesehene Auflage, Meiner, Hamburg 1989, ISBN 3-7873-0930-6, S. 264–267 (nur Übersetzung)
- John Burnet (Hrsg.): Platonis opera, Bd. 4, Clarendon Press, Oxford 1902 (kritische Ausgabe ohne Übersetzung; oft nachgedruckt)
- Heinrich Dörrie, Matthias Baltes (Hrsg.): Der Platonismus in der Antike, Band 4: Die philosophische Lehre des Platonismus. Frommann-Holzboog, Stuttgart-Bad Cannstatt 1996, ISBN 3-7728-1156-6, S. 84–97 (Quellentexte mit Übersetzung) und S. 332–355 (Kommentar)
- Gunther Eigler (Hrsg.): Platon: Politeia. Der Staat (= Platon: Werke in acht Bänden, Bd. 4). 2. Auflage, Wissenschaftliche Buchgesellschaft, Darmstadt 1990, ISBN 3-534-11280-6, S. 544–553, 612–615 (kritische Edition; bearbeitet von Dietrich Kurz, griechischer Text von Émile Chambry, deutsche Übersetzung von Friedrich Schleiermacher)
- Rüdiger Rufener (Hrsg.): Platon: Der Staat. Politeia. Artemis & Winkler, Düsseldorf/Zürich 2000, ISBN 3-7608-1717-3, S. 556–565, 622–625 (griechischer Text nach der Ausgabe von Émile Chambry ohne den kritischen Apparat, deutsche Übersetzung von Rüdiger Rufener, Einführung und Erläuterungen von Thomas Alexander Szlezák)
- Wilhelm Wiegand: Der Staat, Buch VI–X. In: Platon: Sämtliche Werke, Band 2, Lambert Schneider, Heidelberg ohne Jahr (um 1950), S. 205–407, hier: 245–248, 277 f. (nur Übersetzung)
Literatur
- Michael Bordt: Platon. Herder, Freiburg im Breisgau 1999, ISBN 3-451-04761-6, S. 93–127
- Rafael Ferber: Platos Idee des Guten. 2. Auflage, Academia Verlag, Sankt Augustin 1989, ISBN 3-88345-559-8, S. 80–114
- Christoph Quarch: Sein und Seele. Platons Ideenphilosophie als Metaphysik der Lebendigkeit. Interpretationen zu Phaidon und Politeia. Lit Verlag, Münster 1998, ISBN 3-8258-3996-6, S. 39–57
Bibliographie
- Yvon Lafrance: Pour interpréter Platon. Band 1: La Ligne en République VI, 509d–511e. Bilan analytique des études (1804–1984). Les Belles Lettres, Paris 1986, ISBN 2-89007-633-4 (umfangreiche Bibliographie mit Inhaltszusammenfassungen der angeführten Veröffentlichungen)
Anmerkungen
- Platon, Politeia 505a–509d.
- Platon, Politeia 511d8: Die Linie hat einen „obersten“ Teil. Siehe dazu Egil A. Wyller: Der späte Platon, Hamburg 1970, S. 16; Heinrich Dörrie, Matthias Baltes: Der Platonismus in der Antike, Bd. 4, Stuttgart-Bad Cannstatt 1994, S. 333 Anm. 6.
- Platon, Politeia 509d.
- Platon, Politeia 509e–510a.
- Dies ist die Deutung von Wolfgang Wieland: Platon und die Formen des Wissens, 2., erweiterte Auflage, Göttingen 1999, S. 205 f.
- Theodor Ebert: Meinung und Wissen in der Philosophie Platons, Berlin 1974, S. 175 f.
- Wolfgang Wieland: Platon und die Formen des Wissens, 2., erweiterte Auflage, Göttingen 1999, S. 204–206. Vgl. zum Verhältnis von Eikasia und Pistis Vassilis Karasmanis: Plato’s Republic: The Line and the Cave. In: Apeiron Bd. 21 Nr. 3, 1988, S. 147–171, hier: 165–168.
- Platon, Politeia 510c–511b.
- Platon, Politeia 511c–d. Siehe dazu Wolfgang Wieland: Platon und die Formen des Wissens, 2., erweiterte Auflage, Göttingen 1999, S. 208–216; Jürgen Mittelstraß: Die Dialektik und ihre wissenschaftlichen Vorübungen (Buch VI 510b–511e und Buch VII 521c–539d). In: Otfried Höffe (Hrsg.): Platon: Politeia, 3. Auflage, Berlin 2011, S. 175–191, hier: 182–186.
- Rafael Ferber: Platos Idee des Guten, 2. Auflage, Sankt Augustin 1989, S. 91 f.
- Platon, Politeia 511d–e.
- Platon, Politeia 533e–534a.
- Jürgen Mittelstraß: Die Dialektik und ihre wissenschaftlichen Vorübungen (Buch VI 510b–511e und Buch VII 521c–539d). In: Otfried Höffe (Hrsg.): Platon: Politeia, 3. Auflage, Berlin 2011, S. 175–191, hier: 182–186.
- Platon, Politeia 510b, 511b–d; vgl. 533c–e. Siehe dazu Rafael Ferber: Platos Idee des Guten, 2. Auflage, Sankt Augustin 1989, S. 99–111.
- Die Identität des „Voraussetzungslosen“ (anhypótheton) des Liniengleichnisses mit dem „Guten“ des Sonnengleichnisses wird von Platon nicht ausdrücklich festgestellt und ist in der Forschung vereinzelt bestritten worden. Sie ergibt sich aber nach der vorherrschenden Forschungsmeinung aus dem Zusammenhang der Gleichnisse. Zur Begründung siehe Rafael Ferber: Platos Idee des Guten, 2. Auflage, Sankt Augustin 1989, S. 97 f.
- Zur Zurückführung von Grundlagen der Mathematik auf die Idee des Guten siehe Rafael Ferber: Platos Idee des Guten, 2. Auflage, Sankt Augustin 1989, S. 98 f.; Hans Krämer: Die Idee des Guten. Sonnen- und Liniengleichnis (Buch VI 504a–511e). In: Otfried Höffe (Hrsg.): Platon: Politeia, 3. Auflage, Berlin 2011, S. 135–153, hier: 147–151.
- Plutarch, Quaestiones Platonicae 3; siehe dazu Heinrich Dörrie, Matthias Baltes: Der Platonismus in der Antike, Bd. 4, Stuttgart-Bad Cannstatt 1994, S. 88–91, 342 f.
- Alkinoos, Didaskalikos 7, hrsg. von John Whittaker und Pierre Louis: Alcinoos: Enseignement des doctrines de Platon, 2. Auflage, Paris 2002, S. 18 f.
- Siehe dazu Heinrich Dörrie, Matthias Baltes: Der Platonismus in der Antike, Bd. 4, Stuttgart-Bad Cannstatt 1994, S. 344–355.
- Mihaela Girardi-Karšulin: Petrićs Auslegung des Liniengleichnisses. In: Damir Barbarić (Hrsg.): Platon über das Gute und die Gerechtigkeit, Würzburg 2005, S. 203–209.
- Theodor Ebert: Meinung und Wissen in der Philosophie Platons, Berlin 1974, S. 152–159 (Forschungsübersicht); Rafael Ferber: Platos Idee des Guten, 2. Auflage, Sankt Augustin 1989, S. 112 f.; Vassilis Karasmanis: Plato’s Republic: The Line and the Cave. In: Apeiron Bd. 21 Nr. 3, 1988, S. 147–171, hier: 157 f. Weitere Literatur bei Yvon Lafrance: Pour interpréter Platon, Band 1, Paris 1986, Nr. I 4, I 7, I 15, I 16, I 17, I 18, I 24, I 27, I 68, I 80, I 83, I 123, I 141, I 146.
- Siehe dazu Michael Erler: Platon (= Hellmut Flashar (Hrsg.): Grundriss der Geschichte der Philosophie. Die Philosophie der Antike, Band 2/2), Basel 2007, S. 400, 402; Wilhelm Blum: Höhlengleichnisse, Bielefeld 2004, S. 51–53; Oswald Utermöhlen: Die Bedeutung der Ideenlehre für die platonische Politeia, Heidelberg 1967, S. 33–51, 69, 78; Christoph Quarch: Sein und Seele, Münster 1998, S. 58–60; Thomas Alexander Szlezák: Das Höhlengleichnis (Buch VII 514a–521b und 539d–541b). In: Otfried Höffe (Hrsg.): Platon: Politeia, 3. Auflage, Berlin 2011, S. 155–173, hier: 160–162; Hans Lier: Zur Struktur des platonischen Höhlengleichnisses. In: Hermes 99, 1971, S. 209–216; John Malcolm: The Line and the Cave. In: Phronesis 7, 1962, S. 38–45; John S. Morrison: Two Unresolved Difficulties in the Line and the Cave. In: Phronesis 22, 1977, S. 212–231; Ronald Godfrey Tanner: ΔΙΑΝΟΙΑ and Plato's Cave. In: The Classical Quarterly 20, 1970, S. 81–91; Vassilis Karasmanis: Plato’s Republic: The Line and the Cave. In: Apeiron Bd. 21 Nr. 3, 1988, S. 147–171; Karl Bormann: Zu Platon, Politeia 514 b 8–515 a 3. In: Archiv für Geschichte der Philosophie 43, 1961, S. 1–14, hier: 5–14; Miguel A. Lizano-Ordovás: ‚Eikasia’ und ‚Pistis’ in Platons Höhlengleichnis. In: Zeitschrift für philosophische Forschung 49, 1995, S. 378–397.
- Thomas Alexander Szlezák: Das Höhlengleichnis (Buch VII 514a–521b und 539d–541b). In: Otfried Höffe (Hrsg.): Platon: Politeia, 3. Auflage, Berlin 2011, S. 155–173, hier: 161 f.; Konrad Gaiser: Platons ungeschriebene Lehre, 2. Auflage, Stuttgart 1968, S. 89–95; Heinrich Dörrie, Matthias Baltes: Der Platonismus in der Antike, Bd. 4, Stuttgart-Bad Cannstatt 1994, S. 334–340; John A. Brentlinger: The Divided Line and Plato’s ‚Theory of Intermediates’. In: Phronesis 8, 1963, S. 146–166.
- Wolfgang Wieland: Platon und die Formen des Wissens, 2., erweiterte Auflage, Göttingen 1999, S. 207 f., 212, 215; Rafael Ferber: Platos Idee des Guten, 2. Auflage, Sankt Augustin 1989, S. 92; Theodor Ebert: Meinung und Wissen in der Philosophie Platons, Berlin 1974, S. 183 und Anm. 120 und S. 186; Vassilis Karasmanis: Plato’s Republic: The Line and the Cave. In: Apeiron Bd. 21 Nr. 3, 1988, S. 147–171, hier: 155–157.
- Heinrich Dörrie, Matthias Baltes: Der Platonismus in der Antike, Bd. 4, Stuttgart-Bad Cannstatt 1994, S. 337 f. und Anm. 3; Pierre Aubenque: De l’égalité des segments intermédiaires dans la Ligne de la République. In: Marie-Odile Goulet-Cazé u. a. (Hrsg.): Sophies maietores, “Chercheurs de sagesse”. Hommage à Jean Pépin, Paris 1992, S. 37–44; Hans Krämer: Die Idee des Guten. Sonnen- und Liniengleichnis (Buch VI 504a–511e). In: Otfried Höffe (Hrsg.): Platon: Politeia, 3. Auflage, Berlin 2011, S. 135–153, hier: S. 145 Anm. 18.
- Yvon Lafrance: Pour interpréter Platon, Band 1, Paris 1986, Nr. I 4, I 5, I 24, I 41, I 56, I 150. Vgl. Pierre Aubenque: De l’égalité des segments intermédiaires dans la Ligne de la République. In: Marie-Odile Goulet-Cazé u. a. (Hrsg.): Sophies maietores, “Chercheurs de sagesse”. Hommage à Jean Pépin, Paris 1992, S. 37–44, hier: S. 43 und Anm. 16.
- Theodor Ebert: Meinung und Wissen in der Philosophie Platons, Berlin 1974, S. 181–193. Gegen die „Zwei-Welten-Vorstellung“ und den auf ihr basierenden Chorismos-Vorwurf des Aristoteles wandten sich auch John N. Findlay: Plato: The Written and Unwritten Doctrines, London 1974, S. XI f., 32–40, Pierre Aubenque: De l’égalité des segments intermédiaires dans la Ligne de la République. In: Marie-Odile Goulet-Cazé u. a. (Hrsg.): Sophies maietores, “Chercheurs de sagesse”. Hommage à Jean Pépin, Paris 1992, S. 37–44, hier: 44 und Christoph Quarch: Sein und Seele, Münster 1998, S. 42, 55–57, 132–149. In diesem Sinne äußerte sich schon im 19. Jahrhundert Richard Lewis Nettleship: Lectures on the Republic of Plato, London 1963 (Nachdruck; Erstveröffentlichung 1897), S. 238–240.
- Rafael Ferber: Platos Idee des Guten, 2. Auflage, Sankt Augustin 1989, S. 19–48; Michael Erler: Platon (= Hellmut Flashar (Hrsg.): Grundriss der Geschichte der Philosophie. Die Philosophie der Antike, Bd. 2/2), Basel 2007, S. 390, 393; Thomas Alexander Szlezák: Die Idee des Guten in Platons Politeia, Sankt Augustin 2003, S. 95–97.
- Wolfgang M. Ueding: Die Verhältnismäßigkeit der Mittel bzw. die Mittel-Mäßigkeit der Verhältnisse: Das Diagramm als Thema und Methode der Philosophie am Beispiel Platons bzw. einiger Beispiele Platons. In: Petra Gehring u. a. (Hrsg.): Diagrammatik und Philosophie, Amsterdam 1992, S. 13–49, hier: 28–44.