Lenkergeradführung
Eine Lenkergeradführung ist ein spezielles viergliedriges Koppelgetriebe, das dazu dient, „einen Koppel-Punkt auf einer vorgeschrieben Wegstrecke näherungsweise geradezuführen.“[1] Eine exakte Geradführung „ ist nur mit der gleichschenkligen zentrischen Schubkurbel oder mehrgliedrigen Koppelgetrieben ... möglich.“[2]
Zur Anwendung kommt die Geradführung beispielsweise an der Auslegespitze eines Krans (siehe Abbildung), beim Lenker von Evans, wobei sich ein Schreibstift annähernd auf einer Geraden bewegt,[3] oder beim Watt-Gestänge (Lemniskatenlenker).
Beispiele: näherungsweise gerade führend
Aufzählung mit Jahr der Erfindung oder Veröffentlichung, eine Auswahl:
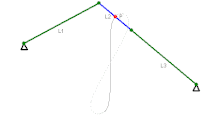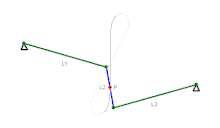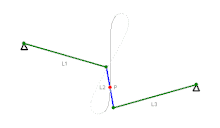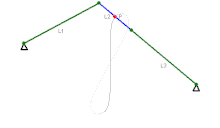Wattgestänge, 1784, wenn Koppel umläuft, dann Rückbewegung auf anderem Lemniskaten-Ast,
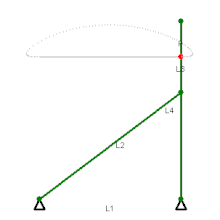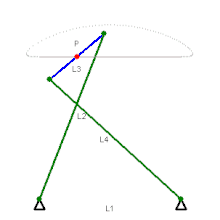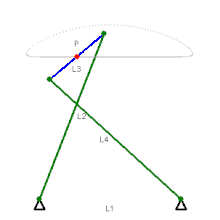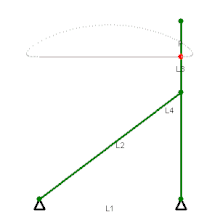Tschebyschow-Mechanismus, 1870er
nichtlineare Rückbewegung, wenn Koppel umläuft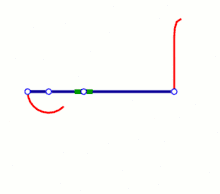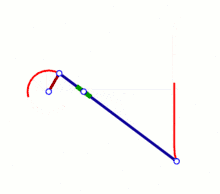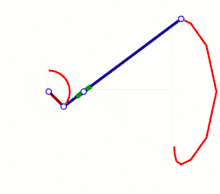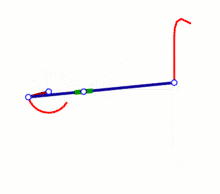
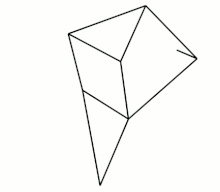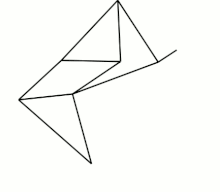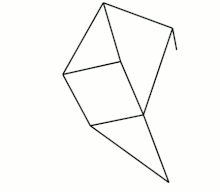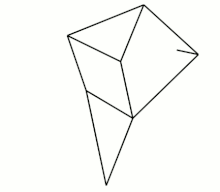
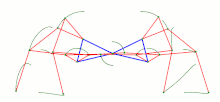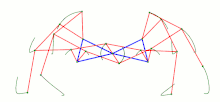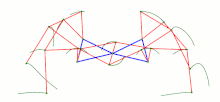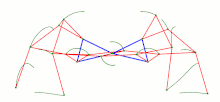vier Klann-Mechanismen, 1998
Imitation von vier nach links gehenden „Füßen“
Das Wattgestänge wurde von James Watt für Dampfmaschinen erfunden und gebraucht. Heute wird es vorwiegend zur vertikalen Führung von Starrachsen in der Querebene an Automobilen gebraucht. Der dafür benutzte Koppelpunkt bewegt sich auf einem Ast einer sehr schlanken Lemniskate. Beim ähnlichen Tschebyschow-Mechanismus geschieht die Rückbewegung auf einem Bogen. Dieser, der Hoecken- und andere Mechanismen mit ähnlicher Koppelpunktbahn wurden als Filmgreifer-Getriebe verwendet.
Die beiden zuletzt abgebildeten Getriebe sind mehr als viergliedrige Koppelgetriebe. Das Strandbeest besteht aus zwei 4-gliedrigen Kurbelschwingen (mit identischer Kurbel und Gestellglied), zwischen deren Schwingen sich ein Zweischlag befindet. Ein Punkt eines der beiden Zweischlagglieder ist der „Fußpunkt“. Der Klann-Mechanismus ist eine Kurbelschwinge mit einem Zweischlag zwischen Koppel und Gestell. Ein Punkt des an der Koppel angelenkten Zweischlagglieds ist der „Fuß“.
Beispiele: exakt gerade führend
Aufzählung mit Jahr der Erfindung oder Veröffentlichung:
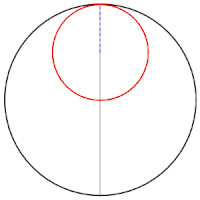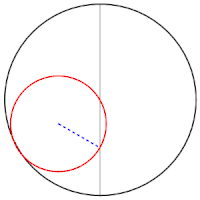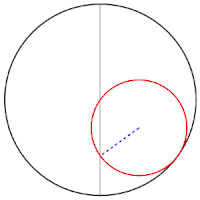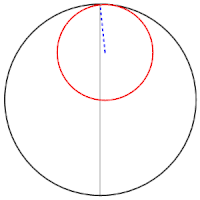Tusi-Paare/Cardanische Kreise
Jeder Punkt des kleinen Kreises bewegt sich auf einem Durchmesser des großen Kreises.
Sarrus-Mechanismus, 1853
als räumliches Koppelgetriebe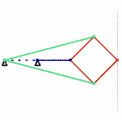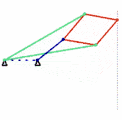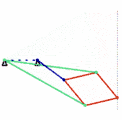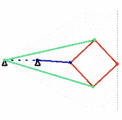
Inversor von Peaucellier, 1864
8-gliedriges Getriebe
Inversor von Hart, 1874/75
6-gliedriges Getriebe
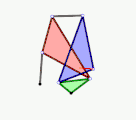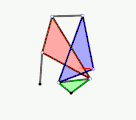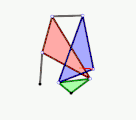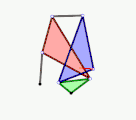Quadruplanar-Inversor von Sylvester und Kempe (1875)
Cardanisches Getriebe als Variation der Cardanischen Kreise
Der Sarrus-Mechanismus ist ein räumliches Koppelgetriebe mit Sonderabmessungen: Seine gleich langen Glieder erlauben nicht nur, dass dieses Getriebe überhaupt beweglich ist, sondern auch, dass sich die Koppel auf einer exakten Geraden bewegt. Es wird heute an faltbaren Schachteln angewendet.
Die anderen abgebildeten Mechanismen repräsentieren die geometrische Inversion: Ein Kreis (Bahn eines Schwingen-Endpunkts) wird durch den Inversionsmittelpunkt in eine Gerade (Bahn des Abtriebs-Punkts) überführt.
Einzelnachweise
- Luck, Modler: Getriebetechnik, Springer, 1990, S. 197
- Johannes Volmer: Getriebetechnik, Verlag Technik, 1968, S. 498
- Siegfried Hildebrand, S. 642
- Dankert/Dankert: Technische Mechanik, Theo Jansens Strandbeest-Mechanismus