Lösungsalgorithmen für Irrgärten
Lösungsalgorithmen für Irrgärten beschreiben Methoden, mit denen automatisiert ein Weg aus einem Irrgarten gefunden werden kann. Dabei gibt es Algorithmen, die einer in einem Irrgarten gefangenen Person ins Freie helfen können, ohne dass sie etwas über den Irrgarten weiß: die zufällige Wegwahl, die Rechte-Hand-Methode, der Pledge-Algorithmus und der Trémaux-Algorithmus. Dagegen setzen Algorithmen wie das Auffüllen von Sackgassen oder das Finden des kürzesten Auswegs voraus, dass der Irrgarten als Ganzes überblickt werden kann.
Irrgärten, in denen man nicht im Kreis gehen kann, werden auch als Standard- oder perfekte Irrgärten bezeichnet. Diese sind äquivalent zu einem Baum in der Graphentheorie. Dies wird intuitiv klar, wenn man sich vorstellt, dass man die Wege eines perfekten Irrgartens geradebiegt. Macht man dies in der richtigen Weise, so sieht das Ergebnis einem Baum sehr ähnlich. Daher spielt die Graphentheorie auch eine große Rolle bei den Lösungsalgorithmen für Irrgärten.
Heuristiken
Zufällige Wegwahl
Diese triviale Methode kann sogar von einem sehr einfachen Roboter durchgeführt werden. Sie besteht einfach darin, so lange geradeaus zu gehen, bis man eine Kreuzung erreicht. Dort entscheidet man sich zufällig für eine Richtung, in die man weitergeht. Weil man bei dieser Methode Wege möglicherweise mehrmals beschreitet, dauert es im Allgemeinen sehr lange, bis man zum Ausgang kommt. Dennoch erreicht man diesen immer.
Rechte-Hand-Methode
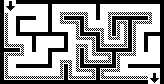

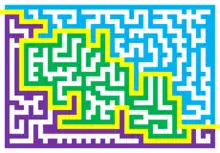
Die Rechte-Hand-Methode ist die bekannteste Regel, einen Irrgarten zu durchqueren. Man legt einfach seine rechte Hand an eine Wand des Irrgartens und hält dann beim Durchlaufen ständigen Kontakt (natürlich kann man statt der rechten auch die linke Hand verwenden). Falls alle Mauern zusammenhängen oder mit der Außenseite verbunden sind – das heißt, der Irrgarten ist „einfach zusammenhängend“ –, garantiert die Rechte-Hand-Methode, dass man entweder einen anderen Ausgang erreicht, oder wieder zum Eingang zurückkehrt.
Es gibt eine einfache topologische Überlegung dafür, dass die Rechte-Hand-Methode wie beschrieben funktioniert: Wenn die Wände des Irrgartens zusammenhängen, kann man sie so lange verformen, bis sie einen Kreis bilden.[1] Die Rechte-Hand-Methode führt in diesem Fall dazu, dass man den Kreis vom Start bis zum Ende umwandert. Verfolgt man diese Idee noch weiter und gruppiert die zusammenhängenden Komponenten des Irrgartens, sind die Grenzen zwischen diesen Komponenten genau die gesuchten Lösungen (siehe nebenstehendes Bild).
Die Rechte-Hand-Methode kann jedoch versagen, wenn der Irrgarten nicht einfach zusammenhängend ist. Dies ist zum Beispiel der Fall, wenn man erst im Inneren des Irrgartens die Hand an die Wand legt und diese Wand zum Beispiel zu einer Säule gehört. Dann wandert man ewig im Kreis. Im ungünstigsten (theoretischen) Fall könnte der Querschnitt der „Säule“ eine fraktale Form haben. In diesem Falle könnte man die Umkreisung der Säule gar nicht vollenden, weil der Umfang dieser Säule unendlich groß wäre. Somit würde man gar nicht feststellen, dass man unfreiwillig versucht, die Säule zu umkreisen – und natürlich kann man in diesem Fall den Irrgarten auch nicht verlassen. (vgl. u. a. Koch.Schneeflocke). Praktisch kann man allerdings keine fraktalen Formen errichten. Auch ist die Rechte-Hand-Methode eventuell nutzlos beim Versuch, ein bestimmtes Ziel innerhalb des Irrgartens zu erreichen.
Die Rechte-Hand-Methode kann auch in Irrgärten mit drei oder mehr Dimensionen angewendet werden. Dazu müssen die Kreuzungen in einer wohldefinierten Weise in eine zweidimensionale Ebene projiziert werden können. Lassen sich zum Beispiel in einem dreidimensionalen Irrgarten „nach oben“ führende in „nach Nordwesten“ führende Gänge umwandeln oder „nach unten“ führende Gänge in „nach Südosten“ führende, kann man die Rechte-Hand-Regel anwenden. Jedoch muss – anders als im zweidimensionalen Fall – die aktuelle Orientierung im Irrgarten immer bekannt sein, um feststellen zu können, in welche Richtung es „nach rechts“ bzw. „nach links“ geht.
Pledge-Algorithmus

Wenn Eingang und Ausgang mit der Außenmauer verbunden sind, kann man mit der Rechten-Hand-Regel auch den Weg durch einen nicht einfach zusammenhängenden Irrgarten finden. Startet man jedoch im Inneren des Irrgartens, kann es passieren, dass man mit der Rechte-Hand-Regel ewig an einer Wand entlang im Kreis läuft, die nicht mit dem Ausgang verbunden ist. Der Pledge-Algorithmus (benannt nach Jon Pledge aus Exeter) löst dieses Problem (siehe „Turtle Geometry: the computer as a medium for exploring mathematics“, Abelson & diSessa, 1980).
Der Pledge-Algorithmus, konzipiert, um Hindernisse zu umrunden, benötigt eine zufällig gewählte Zielrichtung. Trifft man auf ein Hindernis, legt man eine Hand (zum Beispiel immer die rechte) auf das Hindernis und hält auf dem weiteren Weg den Kontakt aufrecht. Dabei zählt man die Winkel, um die man sich beim Vorwärtsgehen von der Zielrichtung wegdreht oder auf die Zielrichtung zudreht. Ist man wieder in Zielrichtung ausgerichtet und ist die Summe der gemachten Drehungen gleich Null, löst man die Hand vom Hindernis und geht wieder geradeaus in Zielrichtung.
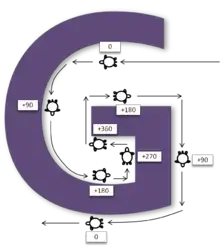
Die Hand wird nur dann von der Wand des Irrgartens genommen, wenn beide Bedingungen erfüllt sind: „Summe der gemachten Drehungen gleich Null“ und „aktuelle Ausrichtung gleich Zielrichtung“. Dadurch vermeidet der Algorithmus, in Fallen zu tappen, die die Form des Großbuchstaben „G“ besitzen. Angenommen, man tritt von rechts in das „G“ ein und wendet sich beim Treffen auf die linke Wand nach links, dreht man sich um 360 Grad. Würde der Algorithmus vorsehen, nun die Wand wieder zu verlassen, da die aktuelle Richtung wieder der Zielrichtung vom Anfang entspricht, so wäre man in einer Endlosschleife gefangen. Denn verlässt man die rechte untere Seite des „G“ und geht nach links, trifft man wieder auf die gekrümmte linke Seite des „G“ und macht erneut eine vollständige Drehung. Der Pledge-Algorithmus verlässt jedoch die rechte untere Seite des „G“ nicht, da die „Summe der gemachten Drehungen“ nicht Null, sondern 360° ist. Stattdessen folgt man weiter der Wand, verlässt das Innere des „G“ wieder und nimmt die Hand von der Wand, wenn man sich an der Unterseite des „G“s befindet und wieder nach links blickt.
Falls es sich um einen endlichen und fairen zweidimensionalen Irrgarten handelt, kann man mit dem Pledge-Algorithmus und einem Kompass von jedem Punkt des Irrgartens aus den Weg ins Freie finden. Umgekehrt funktioniert der Algorithmus jedoch nicht. So ist es mit dem Pledge-Algorithmus im Allgemeinen nicht möglich, vom Eingang aus ein Ziel im Inneren des Irrgartens zu finden.
Trémaux-Algorithmus
Der Trémaux-Algorithmus, erfunden von Charles Pierre Trémaux (1859–1882), benutzt Markierungen, zum Beispiel am Boden, und ist eine effiziente Methode, den Weg aus einem Irrgarten herauszufinden. Der Algorithmus funktioniert garantiert in allen Irrgärten, die wohldefinierte Durchgänge besitzen.[2]
Ein Weg ist entweder unbesucht, einfach oder zweifach markiert. Am Anfang wird eine beliebige Richtung gewählt (wenn es mehr als eine gibt). Dann wird jeder beschrittene Gang von Kreuzung zu Kreuzung zum Beispiel mit einem Strich am Boden markiert. Erreicht man eine Kreuzung, an die man noch nie gekommen ist (erkenntlich daran, dass es keine Markierungen am Boden gibt), wählt man einen beliebigen Gang, um weiterzugehen (und markiert ihn wie beschrieben). Erreicht man dagegen eine markierte Kreuzung und ist der Gang, aus dem man gerade kommt, nur einmal markiert, dreht man um und geht zurück (und markiert den Gang ein zweites Mal). Ansonsten wählt man einen Gang mit möglichst wenigen Markierungen (und markiert ihn wie immer). Erreicht man schließlich sein Ziel, so ist der direkte Weg zurück zum Start mit genau einem Strich markiert.
Sollte es keinen Ausgang geben, erreicht man schließlich wieder den Ausgangspunkt, und alle Gänge des Irrgartens sind mit genau zwei Strichen markiert. In diesem Fall hat man jeden Gang des Irrgartens genau zweimal durchschritten, einmal in jede Richtung. Der erhaltene Weg wird auch als „bidirectional double-tracing“ bezeichnet.
Algorithmus von Gaston Tarry
Der französische Finanzinspekteur Gaston Tarry (1843–1913) entdeckte 1895 folgenden Lösungsalgorithmus für Irrgärten:
- Wenn du einen Gang betrittst, markiere den Eingang mit dem Wort Stopp. Betritt nie einen Gang, der mit Stopp markiert ist.
- Betrittst du das erste Mal eine Kreuzung (daran erkennbar, dass an keinem Gang eine Markierung angebracht ist), markiere den eben verlassenen Gang mit dem Wort zuletzt.
- Gibt es an einer Kreuzung Gänge, die keine Markierung besitzen, wähle einen beliebigen davon, um weiterzugehen. Sollte es keine unmarkierten Gänge mehr geben, betritt den mit zuletzt markierten Gang.
Mit dieser Methode wird der Ausgang garantiert gefunden. Sollte der Irrgarten keinen Ausgang besitzen, wird jede Kreuzung besucht und jeder Gang genau zweimal beschritten (einmal in jede Richtung). Der Algorithmus hält dann wieder am Startpunkt. Die Methode von Tarry ist damit – anders als der Pledge-Algorithmus – auch geeignet, von außen in einen Irrgarten einzutreten und ein Ziel im Inneren zu finden. Der Algorithmus von Trémaux ist ein Spezialfall des Algorithmus von Tarry.[4]
Kenntnis des gesamten Irrgartens
Auffüllen von Sackgassen
Ist der Irrgarten als Ganzes überblickbar, kann der Lösungsweg durch das Auffüllen von Sackgassen gefunden werden. Der Algorithmus ist für Irrgärten auf dem Papier oder in einem Computerprogramm verwendbar, allerdings nicht für Personen innerhalb eines unbekannten Irrgartens. Bei dieser Methode werden zuerst alle Sackgassen aufgesucht und diese dann bis zur nächsten Kreuzung „aufgefüllt“. Folgende Videos veranschaulichen diesen Vorgang:[5][6].
Da jeder Schritt die Topologie des Irrgartens bewahrt, kann das Ziel nicht unabsichtlich vom Start abgeschnitten werden. Außerdem bricht der Algorithmus nicht „zu früh“ ab, da das Ergebnis keine Sackgassen enthalten kann. Werden daher bei einem perfekten Irrgarten – ein Irrgarten, in dem man nicht im Kreis gehen kann – alle Sackgassen aufgefüllt, bleibt nur der Lösungsweg übrig. In einem Irrgarten, in dem man auch im Kreis gehen kann, erhält man alle möglichen Lösungswege.[7]
Den kürzesten Ausweg finden

Bei mehreren möglichen Lösungswegen ist es interessant, den kürzesten Start-Ziel-Weg zu kennen. Dies kann beispielsweise mit einer Breitensuche erreicht werden. Unter Verwendung einer Warteschlange werden dabei Zellen in immer größerer Entfernung vom Startpunkt aufgesucht, bis der Zielpunkt erreicht wird. Von jeder besuchten Zelle muss sich gemerkt werden, wie weit diese vom Startpunkt aus entfernt ist (bzw. von welcher benachbarten Zelle aus die aktuelle Zelle betreten wurde und daher in die Warteschlange kam). Der kürzeste Lösungsweg ergibt sich, indem man vom Zielpunkt aus die besuchten Zellen zurück bis zum Startpunkt verfolgt.
Physikalische Lösungen
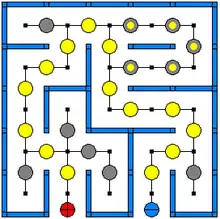
Wenn man in den Eingang eines waagrecht liegenden Irrgartens Wasser einfüllt, oder wenn man in den Eingang eines Irrgartens mit luftdichten Gangdecken Luft einbläst, dann zeigt die stärkste Strömung den kürzesten Weg zum Ausgang an. Der Ausgang muss natürlich dabei als Austrittsöffnung dienen. In den Sackgassen gibt es keine Strömung. Die Strömungen von Wasser oder Luft kann man in dafür geeigneten analogen Schaltungen auch durch elektrische Ströme ersetzen, wie in dem nebenstehenden Bild gezeigt wird. Vermutlich arbeiten auch Schleimpilze in Irrgärten mit einem Lockstoffgradienten, der ähnlich wie eine Wasserströmung funktioniert.
Siehe auch
Weblinks
- Think Labyrinth: Maze algorithms – Details zu diesen und anderen Lösungsalgorithmen für Irrgärten (englisch)
- MazeBlog: Lösungswege durch Bildanalyse finden (englisch)
- Video: Simulation einer Irrgartenlösung
- Video: Schleimpilz löst Irrgarten
- How to Build a Maze (Memento vom 24. Februar 2011 im Internet Archive)
- Video: Simulation eines Roboters, der den Pledge-Algorithmus nutzt
Einzelnachweise
- Maze Transformed – Video auf YouTube
- Edouard Lucas: Récréations Mathématiques Volume I, 1882.
- A. Beutelsbacher: Luftschlösser und Hirngespinste.
- Maze Strategy: Dead End Filling – Video auf YouTube
- Maze Solving algorithm – Video auf YouTube
- Maze Classification