Längster kreuzungsfreier Springerpfad
Der längste kreuzungsfreie Springerpfad ist ein Problem aus dem Gebiet der Unterhaltungsmathematik und eine Art der Schachkomposition.

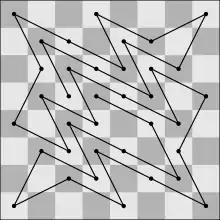
Ziel ist es, einen Springer auf einem leeren Schachbrett in einer möglichst langen Serie von Sprüngen zu bewegen, deren markierter Streckenzug kreuzungsfrei bleibt. Ursprünglich für das Schachbrett erdacht, wurde das Problem auf andere quadratische Bretter n × n erweitert, bzw. für beliebige rechteckige Bretter formuliert. Eine mögliche Variante besteht darin, nach einer möglichst langen geschlossenen Tour zu suchen, bei der der Zielpunkt wieder auf dem Ausgangspunkt liegt.
Allgemeines
Exakte Lösungen des Problems sind nur für Werte n < 10 sicher bekannt. Ein quadratisches Brett muss mindestens die Größe 3 × 3 haben, in diesem Falle sind zwei kreuzungsfreie Züge möglich. Die Zahlenfolge der längsten offenen Pfade für quadratische Bretter (OEIS sequence A003192) beginnt mit
Die Ergebnisse können für kleine n (n < 9) relativ einfach mit einem backtracking-Verfahren nachgewiesen werden. Die Laufzeit des Programms wächst jedoch exponentiell, so dass die Einträge ab n = 9 eventuell noch verbesserbar sind. Eine Übersicht über die längsten bekannten offenen Springerpfade liefert die folgende Tabelle:
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Längster Pfad | 2 | 5 | 10 | 17 | 24 | 35 | 47 | 61 | 76 | 94 | 113 | 135[1] | 158 |
Man kann einige Lösungen in systematischer Weise schrittweise auf immer größere Bretter erweitern und erhält damit eine Abschätzung nach unten für die Mindestlänge eines Pfades auf beliebig großen Brettern. Man findet in dieser Weise, dass die Mindestanzahl der Sprünge (= besuchte Felder-1) im Verhältnis zu den vorhandenen Feldern ebenfalls quadratisch wächst. Für liefert eine gute Näherung, ab ist der längstmögliche Pfad immer mindestens lang.
Verallgemeinerungen
Die Fragestellung kann neben Rechteckbrettern auch für beliebig geformte Polyominos untersucht werden. Die Untersuchung anderer Schachfiguren erbringt keine interessanten Resultate. Verallgemeinert man den gewöhnlichen Springer (1;2), so erhält man dem Märchenschach entliehene Figuren, etwa das Kamel (1;3), das Zebra (2;3) oder die Giraffe (1;4). Die Untersuchung des längsten Pfades ist für diese Figuren ähnlich komplex wie für den Springer.[2]
Man kann die Bedingung aufgeben, dass sich der Springer auf einem Schachbrett bewegt, und stattdessen nur fordern, dass ein nächster Sprung eine Einheitslänge hat und in gewissen Winkeln zum vorhergehenden Sprung geschieht. Statt den Pfad auf ein quadratisches Feld zu begrenzen, sucht man entweder längste Sprünge innerhalb einfacher geometrischer Figuren[3] oder allgemein die längste Sprungserie innerhalb eines vorgegebenen Radius. Die letzte Variante war Inhalt eines Programmierwettbewerbs von Al Zimmermann.[4] Eine Übersicht der Lösungen bietet die Seite enginemonitoring.net.[5]
Neuerdings ist die Untersuchung von kreuzungsfreien Springerpfaden auch für ein dreidimensionales Gitter vorgeschlagen worden.[6] Ein Springer, der in der Zelle (0,0,0) startet, kann dann nicht nur in der xy-Ebene nach (1,2,0) oder (2,1,0), sondern auch in der xz- und yz-Ebene etwa nach (0,2,1) oder (1,0,2) springen. Als begrenzendes Feld definiert man in diesem Fall einen Kubus .
Siehe auch
- Springerproblem, hier wird eine nicht kreuzungsfreie Route über alle Felder eines Schachbretts gesucht
Literatur
- L. D. Yarbrough: Uncrossed knight’s tours. In: Journal of Recreational Mathematics. Band 1, Nr. 3, 1969, S. 140–142.
Weblinks
- Non-Intersecting Paths, by George Jelliss.