Längster Pfad

Die Aufgabe, den einfachen Weg maximaler Länge in einem gegebenen Graphen zu finden, bezeichnet man in der Graphentheorie und der theoretischen Informatik als longest path problem (englisch für Problem des längsten Weges). Ein Weg heißt einfach, wenn er keinen Knoten mehrfach enthält. Die Länge des Weges kann auf zwei Arten gemessen werden: entweder durch die Anzahl der Kanten oder (in einem gewichteten Graphen) durch die Summe der Gewichte seiner Kanten.

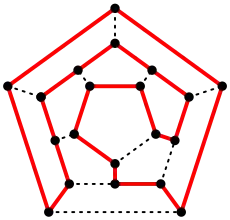
Durch Entfernen einer beliebigen roten Kante erhält man aus diesem Hamiltonkreis einen einfachen Weg maximaler Länge.

Im Gegensatz zum Problem des kürzesten Weges, welches sich in polynomieller Laufzeit lösen lässt, gehört das Problem des längsten Weges zu der Gruppe der NP-schweren Probleme. Dies bedeutet, dass es sich nicht in polynomieller Laufzeit lösen lässt, außer wenn P=NP wäre. Es kann gezeigt werden, dass auch eine Approximation schwierig ist. Das Problem kann jedoch für gerichtete, nicht-zyklische Graphen mithilfe einer topologischen Sortierung in linearer Zeit gelöst werden.[1] Ein wichtiges Anwendungsgebiet ist das Finden des kritischen Weges in Planungsaufgaben.

NP-Schwere

Die NP-Schwere des ungewichteten längsten Weges kann mit Hilfe des Hamiltonwegproblems gezeigt werden. Ein Graph $G$ hat nur dann einen Hamiltonweg, wenn sein längster Weg die Länge $n-1$ hat, wobei $n$ die Anzahl der Knoten in $G$ ist. Da das Hamiltonwegproblem NP-vollständig ist, ist auch die Entscheidungsversion des längsten Weges NP-vollständig. In der Entscheidungsversion besteht der Input aus dem Graphen $G$ und einer Zahl $k$ . Der Output ist "ja", sofern $G$ einen einfachen Pfad mit $k$ oder mehr Kanten enthält.[2]

Wenn das Problem des längsten Weges in polynomieller Laufzeit gelöst werden könnte, so könnte damit die Entscheidungsversion durch einen Vergleich der Länge des längsten Weges mit $k$ gelöst werden. Daher ist das Problem des längsten Weges NP-schwer. Die Frage "Gibt es in einem gegebenen Graphen einen Pfad mit mindestens k Kanten" ist NP-vollständig.[3]

In einem gewichteten vollständigen Graphen ist das Problem des gewichteten längsten Weges äquivalent zum Problem des Handlungsreisenden, da der längste Weg notwendigerweise alle Knoten enthält.[4]

Einzelnachweise

Noltemeier, Hartmut: Graphentheoretische Konzepte und Algorithmen. 3. Auflage. Vieweg+Teubner Verlag, Wiesbaden 2012, ISBN 978-3-8348-1849-2, S. 191 f.
Alexander Schrijver: Combinatorial Optimization: Polyhedra and Efficiency, Volume 1. Band 24. Springer, 2003, ISBN 3-540-44389-4, S. 114.
Thomas H Cormen, Charles E Leiserson, Ronald L Rivest, Clifford Stein (Hrsg.): Introduction To Algorithms. 2. Auflage. MIT Press, 2003, ISBN 0-262-03293-7, S. 978.
Eugene Lawler: Combinatorial Optimization: Networks and Matroids. Courier Dover Publications, 2001, ISBN 0-486-41453-1, S. 64.

Weblinks

"Find the Longest Path", song by Dan Barrett

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Noltemeier, Hartmut: Graphentheoretische Konzepte und Algorithmen. 3. Auflage. Vieweg+Teubner Verlag, Wiesbaden 2012, ISBN 978-3-8348-1849-2, S. 191 f.

[2] Alexander Schrijver: Combinatorial Optimization: Polyhedra and Efficiency, Volume 1. Band 24. Springer, 2003, ISBN 3-540-44389-4, S. 114.

[3] Thomas H Cormen, Charles E Leiserson, Ronald L Rivest, Clifford Stein (Hrsg.): Introduction To Algorithms. 2. Auflage. MIT Press, 2003, ISBN 0-262-03293-7, S. 978.

[4] Eugene Lawler: Combinatorial Optimization: Networks and Matroids. Courier Dover Publications, 2001, ISBN 0-486-41453-1, S. 64.