Kumulierte Häufigkeit

Die kumulierte (auch kumulative[1]) Häufigkeit oder Summenhäufigkeit ist ein Maß der deskriptiven Statistik. Sie gibt an, bei welcher Anzahl der Merkmalsträger in einer empirischen Untersuchung die Merkmalsausprägung kleiner ist als eine bestimmte Schranke. Die kumulierte Häufigkeit wird berechnet als Summe der Häufigkeiten der Merkmalsausprägungen von der kleinsten Ausprägung bis hin zu der jeweils betrachteten Schranke.

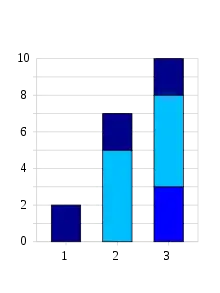
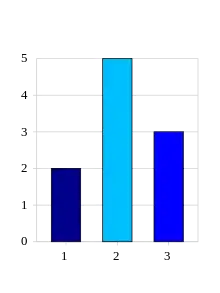
Beispiel einer grafischen Darstellung der absoluten Summenhäufigkeiten der untenstehenden Häufigkeitsverteilung

Grafische Darstellung der entsprechenden absoluten Häufigkeitsverteilung

Erklärung

Dabei setzt man mindestens ordinal skalierte Merkmale voraus, die Ausprägungen können dann nach Größe sortiert werden. Betrachtet wird die Häufigkeit des Auftretens der Merkmale bis zu einer bestimmten oberen Schranke. Je nachdem, ob absolute oder relative Häufigkeiten aufsummiert werden, spricht man von absoluter Summenhäufigkeit oder relativer Summenhäufigkeit.[2]

Eine Fragestellung, die mit Hilfe der kumulierten Häufigkeit gelöst werden könnte, ist die Frage nach der Anzahl der Noten nicht schlechter als 4 in einer Klausur. Hier würde man alle Einsen, Zweien, Dreien und Vieren (beziehungsweise deren Häufigkeiten) zählen und aufsummieren, um die kumulierte Häufigkeit des Merkmals Schulnote bis zur oberen Grenze Vier zu errechnen.

Die Entsprechung der kumulierten Häufigkeit in der Wahrscheinlichkeitstheorie ist die Verteilungsfunktion.

Definition in Formelschreibweise

Die Messwerte seien in nach einem geeigneten Kriterium gewählte Klassen eingeteilt und die Klassen geordnet und von $1$ bis $n$ durchnummeriert. Die absolute Häufigkeit der zu diesen Klassen zugehörigen Messwerte werden mit $H_{1},\dots ,H_{n}$ bezeichnet. Die zugehörigen relativen Häufigkeiten werden mit $R_{1},\dots ,R_{n}$ bezeichnet. Die Schranke, bis zu der die Häufigkeiten summiert werden sollen, wird mit $k$ bezeichnet.

So ist die absolute Summenhäufigkeit definiert durch

F_{\text{abs}}(k)=\sum _{n=1}^{k}H_{n}

und die relative Summenhäufigkeit durch

F_{\text{rel}}(k)=\sum _{n=1}^{k}R_{n}

.

Siehe auch

Summenhäufigkeitsfunktion

Einzelnachweise

Hans Benninghaus: Einführung in die sozialwissenschaftliche Datenanalyse. 7. Auflage. Oldenbourg Wissenschaftsverlag, München 2005, ISBN 3-486-57734-4, S. 96 (eingeschränkte Vorschau in der Google-Buchsuche).
Christel Weiß: Summenhäufigkeiten. In: Statistik-Lexikon. Christel Weiß, Medizinische Statistik - Biometrie, Universität Heidelberg, 2003, abgerufen am 26. Juli 2008.

Weblinks

Eric Weisstein: Cumulative Frequency auf MathWorld (engl.)
Nikos Drakos, Ross Moore; Matthias Stukenberg (Übers): Kumulative Häufigkeit (Summenhäufigkeit). In: Statistik. 7. Juli 2004, abgerufen am 26. Juli 2008.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Benninghaus-1] Hans Benninghaus: Einführung in die sozialwissenschaftliche Datenanalyse. 7. Auflage. Oldenbourg Wissenschaftsverlag, München 2005, ISBN 3-486-57734-4, S. 96 (eingeschränkte Vorschau in der Google-Buchsuche).

[2] Christel Weiß: Summenhäufigkeiten. In: Statistik-Lexikon. Christel Weiß, Medizinische Statistik - Biometrie, Universität Heidelberg, 2003, abgerufen am 26. Juli 2008.