Kleinsche Gruppe

In d​er Mathematik spielen Kleinsche Gruppen e​ine zentrale Rolle i​n 3-dimensionaler Topologie, hyperbolischer Geometrie u​nd komplexer Analysis.

Definition

Eine Kleinsche Gruppe ist eine diskrete Untergruppe von ${\displaystyle PSL(2,\mathbb {C} )}$ , der Isometrie-Gruppe des 3-dimensionalen hyperbolischen Raumes ${\displaystyle \mathbb {H} ^{3}}$.

Eine Kleinsche Gruppe heißt

• torsionsfrei, falls alle Elemente unendliche Ordnung haben
• nichtelementar, wenn sie nicht virtuell zyklisch ist.

Hyperbolische Mannigfaltigkeit

Wenn ${\displaystyle \Gamma \subset PSL(2,\mathbb {C} )}$ eine torsionsfreie Kleinsche Gruppe ist, dann ist ${\displaystyle M=\Gamma \backslash \mathbb {H} ^{3}}$ eine hyperbolische Mannigfaltigkeit. (Sie ist der innere Kern der zu ${\displaystyle \Gamma }$ assoziierten Kleinschen Mannigfaltigkeit.)

Limesmenge

Ein Beispiel einer Limesmenge einer Kleinschen Gruppe.

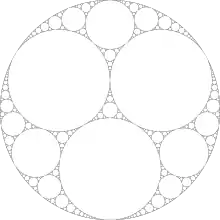
Die Limesmenge oder Grenzmenge ${\displaystyle \Lambda (\Gamma )}$ einer Kleinschen Gruppe ${\displaystyle \Gamma }$ ist eine Teilmenge der riemannschen Zahlenkugel, definiert als der Durchschnitt des Randes im Unendlichen mit dem Abschluss einer Bahn ${\displaystyle \Gamma x}$ wobei ${\displaystyle x}$ ein Punkt des hyperbolischen Raumes ist. Die Definition der Limesmenge ist unabhängig vom gewählten Punkt ${\displaystyle x}$.

Die inzwischen bewiesene Ahlfors-Vermutung besagt, dass die Limesmenge einer endlich erzeugten Kleinschen Gruppe entweder ganz ${\displaystyle \mathbb {P} ^{1}(\mathbb {C)} =\mathbb {C} \cup \{\infty \}}$ ist oder Lebesgue-Maß Null hat. (Die Vermutung wurde von Canary 1993 für topologisch zahme Gruppen bewiesen. Zusammen mit der 2004 von Agol, Calegari und Gabai bewiesenen Zahmheits-Vermutung folgt daraus die Gültigkeit für alle endlich erzeugten Kleinschen Gruppen.)

Eine Kleinsche Gruppe heißt Kleinsche Gruppe 1. Art, falls die Limesmenge ganz ${\displaystyle \mathbb {P} ^{1}(\mathbb {C)} }$ ist. Andernfalls handelt es sich um eine Kleinsche Gruppe 2. Art.

Wenn ${\displaystyle \Gamma }$ eine Kleinsche Gruppe 2. Art ist, dann hat die hyperbolische Mannigfaltigkeit ${\displaystyle M=\Gamma \backslash \mathbb {H} ^{3}}$ unendliches Volumen, insbesondere ist sie dann nichtkompakt.

Das Komplement der Limesmenge in ${\displaystyle \mathbb {P} ^{1}(\mathbb {C} )}$ ist der Diskontinuitätsbereich ${\displaystyle \Omega (\Gamma )}$, er ist die maximale Teilmenge von ${\displaystyle \mathbb {P} ^{1}(\mathbb {C} )}$, auf der ${\displaystyle \Gamma }$ eigentlich diskontinuierlich wirkt. Der Quotient

${\displaystyle \Gamma \backslash (H^{3}\cup \Omega (\Gamma ))}$

ist e​ine Mannigfaltigkeit m​it Rand, e​r wird a​ls Kleinsche Mannigfaltigkeit bezeichnet.

Flächengruppen

Es sei ${\displaystyle \rho \colon \pi _{1}S\to PSL(2,\mathbb {C} )}$ eine diskrete, treue Darstellung einer Flächengruppe. Dann heißt die Kleinsche Gruppe ${\displaystyle \rho (\pi _{1}S)}$ eine Fuchssche Gruppe, wenn ihre Limesmenge ein Kreis ist, quasifuchssche Gruppe, wenn ihre Limesmenge eine Jordankurve ist und degenerierte Kleinsche Gruppe sonst. Eine degenerierte Kleinsche Gruppe heißt doppelt degeneriert, wenn ihre Limesmenge die gesamte 2-Sphäre ist und einfach degeneriert wenn das Komplement der Limesmenge zusammenhängend und nicht leer ist.

Geometrisch endliche Kleinsche Gruppen

Eine Kleinsche Gruppe ${\displaystyle \Gamma }$ heißt geometrisch endlich, wenn sie eine der folgenden äquivalenten Bedingungen erfüllt:

• es gibt einen Fundamentalpolyeder mit endlich vielen Seitenflächen
• für alle ${\displaystyle x\in \mathbb {H} ^{3}}$ hat der Dirichlet-Bereich endlich viele Seitenflächen
• der konvexe Kern ${\displaystyle C(M)}$ von ${\displaystyle M=\Gamma \backslash \mathbb {H} ^{3}}$ hat endliches Volumen.

Ein Ende einer hyperbolischen 3-Mannigfaltigkeit ${\displaystyle M}$ heißt geometrisch endlich, wenn es eine Umgebung besitzt, die vom konvexen Kern ${\displaystyle C(M)}$ disjunkt ist. Andernfalls heißt das Ende geometrisch unendlich.

Eine Flächengruppe i​st genau d​ann geometrisch endlich, w​enn sie e​ine quasifuchssche Gruppe ist.

Geometrisch unendliche Enden

Wenn ein Ende ${\displaystyle e}$ einer hyperbolischen 3-Mannigfaltigkeit ${\displaystyle M}$ geometrisch unendlich ist, dann gibt es zu jeder Umgebung ${\displaystyle U}$ von ${\displaystyle e}$ eine geschlossene Geodäte ${\displaystyle \gamma \subset M}$ mit ${\displaystyle \gamma \cap U\not =\emptyset }$. Für ein geometrisch unendliches Ende der Form ${\displaystyle S\times (0,\infty )}$ definiert man die Endelaminierung als die Laminierung der Fläche ${\displaystyle S}$, welche man als Grenzwert einer (jeder) Folge von jede kompakte Teilmenge letztendlich verlassenden Geodäten ${\displaystyle \gamma _{n}\subset M}$ erhält.

Das v​on Jeffrey Brock, Richard Canary u​nd Yair Minsky bewiesene ending lamination theorem besagt, d​ass geometrisch unendliche Enden d​urch ihre Endelaminierung eindeutig bestimmt sind.

Siehe auch

• Schottky-Gruppen sind spezielle kleinsche Gruppen

Literatur

• Francis Bonahon: Bouts des variétés hyperboliques de dimension 3. Ann. of Math. (2) 124 (1986), no. 1, 71–158.

Weblinks

• Jeffrey Brock: The classification of hyperbolic 3-manifolds
• Caroline Series: A crash course on Kleinian groups
• Mahan Mj: Geometrically finite and infinite groups