Ende (Topologie)

In d​er Mathematik s​ind die Enden e​ines topologischen Raumes anschaulich gesprochen d​ie Zusammenhangskomponenten d​es "Randes i​m Unendlichen". Formal definiert werden s​ie als Äquivalenzklassen v​on Komplementen kompakter Mengen.

Definition

Sei ${\displaystyle X}$ ein (lokal zusammenhängender, zusammenhängender, lokal kompakter, Hausdorffscher) topologischer Raum.

Wir betrachten die Familie ${\displaystyle {\mathcal {U}}}$ aller absteigenden Folgen

${\displaystyle (U_{1}\supset U_{2}\supset U_{3}\supset \ldots )}$

zusammenhängender, offener Mengen m​it kompaktem Rand, für die

${\displaystyle \bigcap _{i=1}^{\infty }{\overline {U_{i}}}=\emptyset }$

gilt.

Auf ${\displaystyle {\mathcal {U}}}$ definieren wir eine Äquivalenzrelation ${\displaystyle \sim }$ durch

${\displaystyle (U_{1}\supset U_{2}\supset U_{3}\supset \ldots )\sim (V_{1}\supset V_{2}\supset V_{3}\supset \ldots )\Longleftrightarrow \forall n\exists k\colon V_{k}\subset U_{n},U_{k}\subset V_{n}}$.

Die Äquivalenzklassen der Äquivalenzrelation ${\displaystyle \sim }$ auf ${\displaystyle {\mathcal {U}}}$ heißen Enden des topologischen Raumes ${\displaystyle X}$.

Als Umgebungen e​ines Endes werden d​ie offenen Mengen i​n der jeweiligen Äquivalenzklasse bezeichnet.

Charakterisierung über Komplemente von Kompakta

(Specker, Raymond): Ein Raum hat mindestens ${\displaystyle k}$ Enden, wenn es eine offene Menge mit kompaktem Abschluss gibt, deren Komplement ${\displaystyle k}$ Zusammenhangskomponenten hat.

Fundamentalgruppe eines Endes

Die Fundamentalgruppe eines Endes ${\displaystyle E}$ wird definiert als der projektive Limes der Fundamentalgruppen der Umgebungen ${\displaystyle U_{i}}$ des Endes ${\displaystyle E}$:

${\displaystyle \pi _{1}(E)=\varprojlim _{i\in I}\pi _{1}(U_{i})}$.

Beispiele

• Die Zahlengerade ${\displaystyle \mathbb {R} ^{1}}$ hat zwei Enden.
• Für ${\displaystyle n\geq 2}$ hat der ${\displaystyle \mathbb {R} ^{n}}$ ein Ende.
• Sei ${\displaystyle M}$ das Innere einer kompakten Mannigfaltigkeit ${\displaystyle {\overline {M}}}$ mit Rand ${\displaystyle \partial {\overline {M}}}$, also ${\displaystyle M={\overline {M}}-\partial {\overline {M}}}$. Dann entsprechen die Enden von ${\displaystyle M}$ den Zusammenhangskomponenten von ${\displaystyle \partial {\overline {M}}}$.

Der Cayleygraph der freien Gruppe mit zwei Erzeugern a und b

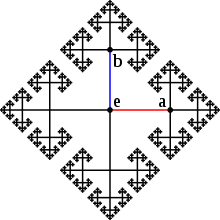
• Sei ${\displaystyle X}$ der Cayley-Graph einer nichtabelschen freien Gruppe. Dann hat ${\displaystyle X}$ unendlich viele Enden, es gibt eine Bijektion der Menge der Enden auf eine Cantormenge.
• Nach einem Satz von Freudenthal hat der Cayley-Graph einer Gruppe entweder unendlich viele oder höchstens 2 Enden.

Literatur

• Hughes, Bruce; Ranicki, Andrew: Ends of complexes. Cambridge Tracts in Mathematics, 123. Cambridge University Press, Cambridge, 1996. ISBN 0-521-57625-3
• Freudenthal, Hans: Über die Enden diskreter Räume und Gruppen. Comment. Math. Helv. 17, (1945). 1–38. online (PDF; 3,0 MB)