Klassendiagramm
Ein Klassendiagramm ist ein Strukturdiagramm der Unified Modeling Language (UML) zur grafischen Darstellung (Modellierung) von Klassen, Schnittstellen sowie deren Beziehungen. Eine Klasse ist in der Objektorientierung ein abstrakter Oberbegriff für die Beschreibung der gemeinsamen Struktur und des gemeinsamen Verhaltens von Objekten (Klassifizierung). Sie dient dazu, Objekte zu abstrahieren. Im Zusammenspiel mit anderen Klassen ermöglichen sie die Modellierung eines abgegrenzten Systems in der objektorientierten Analyse und Entwurf.
| Strukturdiagramme der UML |
|---|
| Klassendiagramm |
| Komponentendiagramm |
| Kompositionsstrukturdiagramm |
| Objektdiagramm |
| Paketdiagramm |
| Profildiagramm |
| Verteilungsdiagramm |
| Verhaltensdiagramme der UML |
| Aktivitätsdiagramm |
| Anwendungsfalldiagramm |
| Interaktionsübersichtsdiagramm |
| Kommunikationsdiagramm |
| Sequenzdiagramm |
| Zeitverlaufsdiagramm |
| Zustandsdiagramm |
Seit den 1990er Jahren werden Klassendiagramme meistens in der Notation der UML dargestellt. Das Klassendiagramm ist eine der 14 Diagrammarten der UML, einer Modellierungssprache für Software und andere Systeme.
Notation in der Unified Modeling Language
Klassen
Klassen werden durch Rechtecke dargestellt, die entweder nur den Namen der Klasse (fett gedruckt) tragen oder zusätzlich auch Attribute, Operationen und Eigenschaften spezifiziert haben. Dabei werden diese drei Rubriken (engl. compartment) – Klassenname, Attribute, Operationen/Eigenschaften – jeweils durch eine horizontale Linie getrennt. Wenn die Klasse keine Eigenschaften oder Operationen besitzt, kann die unterste horizontale Linie entfallen. Oberhalb des Klassennamens können Schlüsselwörter (engl. keyword) in Guillemets und unterhalb des Klassennamens in geschweiften Klammern zusätzliche Eigenschaften (wie {abstrakt}) stehen.
Die Attribute werden wie folgt spezifiziert:
[Sichtbarkeit] [/] name [: Typ] [ Multiplizität ] [= Vorgabewert] [{eigenschaftswert*}]
Daraus folgt, dass in der UML ausschließlich der Name eines Attributs angegeben werden muss, und zwar eindeutig innerhalb einer Klasse. Klassenattribute werden unterstrichen. Darüber hinaus sind bei Attributnamen sämtliche Zeichen erlaubt, auch wenn in einigen Programmiersprachen beispielsweise Umlaute verboten sind.
Operationen werden in ähnlicher Art und Weise spezifiziert:
[Sichtbarkeit] name [({Parameter})] [: Rückgabetyp] [{eigenschaftswert*}]
Zudem wird ein Parameter wie folgt aufgebaut:
[Übergaberichtung] name : Typ [ Multiplizität ] [= Vorgabewert] [{eigenschaftswert*}]
Die Namensgebung und der Zeichenraum sind hier genauso wie bei den Attributsspezifikationen. Klassenoperationen werden auch hier unterstrichen. Den „Pseudotyp“ void gibt es in der UML nicht, daher muss in einem solchen Fall der Rückgabetyp weggelassen werden. Ansonsten können bei Attributen und Operationen sämtliche primitiven Typen sowie selbst definierte Klassen oder Interfaces als Typ bzw. Rückgabetyp verwendet werden.
Die Sichtbarkeit von Operationen und Attributen wird wie folgt gekennzeichnet:
- „+“ für public – (engl. öffentlich), unbeschränkter Zugriff
- „#“ für protected – (engl. geschützt), Zugriff nur von der Klasse sowie von Unterklassen (Klassen, die erben)
- „−“ für private – (engl. privat), nur die Klasse selbst kann es sehen
- „~“ für package – (engl. Paket), innerhalb des Pakets sichtbar (nur in wenigen Programmiersprachen, etwa Java und C#, implementierbar)
Mögliche Eigenschaften sind:
- ordered
- die Daten werden geordnet zurückgegeben
- redefines <Operationsname> (nur bei Operationen)
- diese Operation überschreibt die geerbte Operation <Operationsname>
- read-only
- auf diese Variable kann nur lesend zugegriffen werden
Die Übergaberichtungen:
- in
- Der übergebene Parameter wird nur gelesen (Standard, wenn nichts angegeben wurde).
- out
- Der übergebene Parameter wird beschrieben, ohne ihn vorher zu lesen.
- inout
- Der übergebene Parameter wird gelesen bzw. verarbeitet und beschrieben, beispielsweise um das Ergebnis zurückzugeben.
Die folgenden Abbildungen zeigen zwei Varianten der grafischen Notation für eine Klasse. Abhängig davon, ob eine Klasse in einem Klassendiagramm für ein Design- oder für ein Analysemodell gezeichnet wird, können mehr oder weniger Details dargestellt werden.
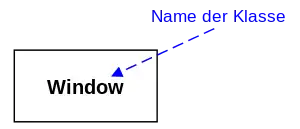Einfachste Form der Darstellung für eine Klasse
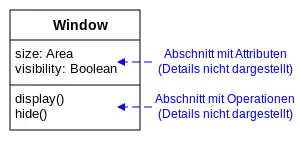Zusätzliche Darstellung von Attributen und Operationen
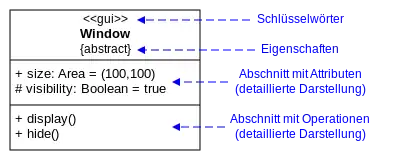
Abstrakte Klassen sind Klassen, von denen keine Instanz angelegt werden kann. Abstrakte Klassen sehen in UML wie normale Klassen aus. Um sie zu unterscheiden, steht unterhalb des Klassennamens das Wort abstract in geschweiften Klammern. Alternativ kann der Klassenname auch kursiv geschrieben werden, wenn dies gut erkennbar ist.
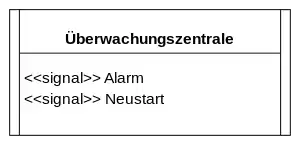
Eine aktive Klasse wird mit einem doppelten linken und rechten Rand gezeichnet.
Einige Programmiersprachen ermöglichen eine Parametrisierung von Klassenschablonen (Class Templates), um Objekte basierend auf diesen Vorlagenparametern zu erzeugen. Die UML bietet dafür die Notation für Template Arguments an. Dabei werden die Vorlagenparameter in einem gestrichelten Rechteck überlappend an die rechte obere Ecke der Klasse eingetragen. Im Beispiel ist eine Klasse „Vector“ mit dem Vorlagenparametertyp „int“ und dem Parameternamen „T_VALUE“ eingetragen.
Schnittstellen
Eine Schnittstelle wird ähnlich wie eine Klasse mit einem Rechteck dargestellt, zur Unterscheidung aber mit dem Schlüsselwort interface gekennzeichnet. Schnittstellen können seit der UML 2 auch Attribute besitzen.[1]
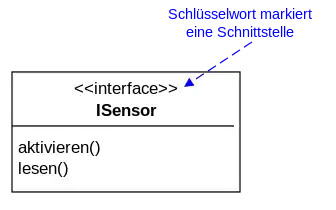Eine Schnittstelle wird mit dem Schlüsselwort <<interface>> markiert
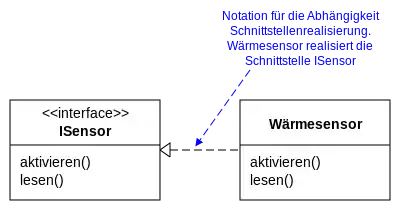Angebotene Schnittstelle, dargestellt mit einer Schnittstellenrealisierungsbeziehung
Wichtige Beziehungen
Generalisierung
.svg.png.webp)
Eine Generalisierung in der UML ist eine gerichtete Beziehung zwischen einer generelleren und einer spezielleren Klasse. Exemplare der spezielleren Klasse sind damit auch Exemplare der generelleren Klasse. Konkret bedeutet dies, dass die speziellere Klasse implizit über alle Merkmale (Struktur- und Verhaltensmerkmale) der generelleren Klasse verfügt – implizit deshalb, weil diese Merkmale in der spezielleren Klasse nicht explizit deklariert werden. Man sagt, dass die speziellere Klasse sie von der generelleren Klasse „erbt“ oder „ableitet“.
Eine Generalisierung wird als durchgezogene Linie zwischen den beiden beteiligten Classifiern dargestellt. Am Ende mit dem generelleren Classifier wird eine geschlossene, nicht ausgefüllte Pfeilspitze gezeichnet.
In gängigen objektorientierten Programmiersprachen entspricht dies dem Konzept der Vererbung, wobei der Pfeil auf die Oberklasse zeigt.
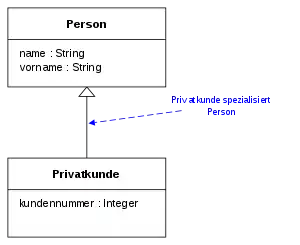Generalisierung in einem Beispiel angewandt
Assoziation
Eine Assoziation beschreibt eine Beziehung zwischen zwei oder mehr Klassen. An den Enden von Assoziationen sind häufig Multiplizitäten vermerkt. Diese drücken aus, wie viele dieser Objekte in Relation zu den anderen Objekten dieser Assoziation stehen.
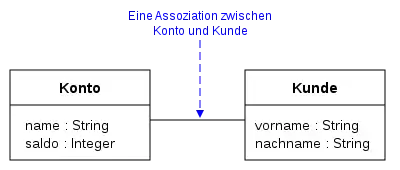Beispiel für eine binäre Assoziation
Beispiel für eine reflexive Assoziation
Komposition und Aggregation
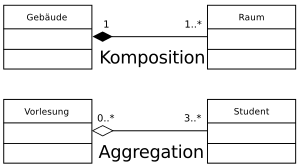
Eine Beziehung zwischen Klassen, die relativ häufig benötigt wird, ist die Beziehung zwischen einem Ganzen und seinen Teilen. Die UML sieht dafür zwei spezielle Assoziationen vor: die Aggregation und die speziellere Komposition. Durch Wahl der Aggregation oder der Komposition wird die Beziehung der Teile zu ihrem Ganzen beschrieben.
In der grafischen Darstellung einer Komposition dekoriert eine ausgefüllte Raute das Ende mit der Multiplizität 1 (oder 1..1), das mit dem Ganzen verbunden ist. Im Fall der Aggregation ist es eine nicht ausgefüllte Raute mit einer Kardinalität von 0..* .
Die Komposition ist ein Spezialfall der Aggregation und bildet den Fall ab, bei dem die Teile nicht ohne das Ganze existieren können. Man spricht auch davon, dass die Teile vom Ganzen existenziell abhängig sind (Existenzabhängigkeit). Im Gegensatz dazu können Teile in einer Aggregation sehr wohl existieren, wenn auch das Ganze (noch) nicht existiert. Die Teile sind hier nicht existenziell vom Ganzen abhängig.
Wird eine solche Beziehung modelliert, bedeutet dies immer, dass das Ganze eine Kardinalität von 0..1 oder von 1..1 besitzt; die Teile sind Bestandteil genau eines Ganzen oder (noch) freistehend – sie gehören jedoch niemals zu mehreren „Ganzen“. Der Fokus liegt hierbei eher auf den Teilen. Der Modellierer will durch eine Aggregation/Komposition aussagen, dass die Teile von ihrem Ganzen abhängig sind.
Dabei definiert der Unterschied in der Kardinalität (0..* oder 1..1), ob eine Aggregation oder der Spezialfall Komposition vorliegt. Eine Komposition liegt genau dann vor, wenn die Kardinalität am Ganzen 1..1 lautet, oder wie im Bild abgekürzt einfach nur 1. Eine Aggregation liegt vor, wenn die Kardinalität 0..* lautet.
Für das Beispiel heißt die Existenzabhängigkeit folgendes:
- (Komposition:) Ein Raum kann nicht ohne Gebäude existieren.
- (Aggregation:) Ein Student kann ohne Vorlesung existieren.
Dennoch bestehen die linken Entitäten aus den rechten Entitäten:
- Ein Gebäude besteht aus Räumen. (Im Beispiel aus mindestens einem Raum; ist als Kardinalität auch 0 Räume zulässig, so ist die Beziehung dennoch eine Komposition.)
- Eine Vorlesung besteht aus Studenten. (Im Beispiel aus mindestens drei Studenten; ist als Kardinalität auch 0 Studenten zulässig, so ist die Beziehung dennoch eine Aggregation.)
In Hinblick auf eine „besteht aus“-Beziehung unterscheiden sich Komposition und Aggregation nicht. Dies ist genau das, was sie vereint. Sie unterscheiden sich jedoch in der „kann ohne sein Ganzes existieren“-Beziehung.
Liegt eine Komposition vor, spricht man auch von einer referenziellen Integrität, die für einen Teil angibt, dass es vom Ganzen abhängig ist.
Das „Ganze“ darf zusätzliche Beziehungen zu anderen Klassen oder weitere eigene Attribute besitzen – es muss nicht ausschließlich aus Teilen einer Klasse bestehen.
Formale Semantik
Rumbaugh, Jacobson und Booch fordern eine eher minimal definierte, mengentheoretische Semantikbeschreibung.[2] Demnach ist eine Konfiguration (englisch snapshot) eines UML-Klassendiagrammes eine Menge von Objekten der in dem Diagramm vorhandenen Klassen. Eine Konfiguration ist konsistent, wenn alle in dem Diagramm angegebenen Einschränkungen eingehalten werden, wie z. B. Multiplizitäten oder OCL Constraints.
Klassen und Attribute
In jeder Konfiguration wird eine Klasse als Menge ihrer Objekte beschrieben. Wenn der Name einer Klasse ist, dann ist eine Menge. Diese Menge darf auch leer sein, wenn es kein Objekt gibt.
Wenn ein Attribut vom Typ einer Klasse mit dem Klassennamen ist, dann ist eine partielle Funktion von der Menge der Objekte in die Menge der Objekte des Attributstyps . Die Funktion muss partiell sein, da sie für (noch) nicht initialisierte Attribute undefiniert ist. Klassenattribute werden genauso behandelt, haben aber die zusätzliche Einschränkung, dass alle Objekte einer Klasse auf dasselbe Objekt des Attributtyps abgebildet werden müssen.
Wurde zusätzlich eine Multiplizität eines Attributes definiert mit dem Intervall , dann ist eine Relation mit , mit der zusätzlichen Einschränkung, dass für jedes gilt.
Falls eine Klasse mit Namen eine Unterklasse von der Klasse mit Namen ist, dann gilt:
Assoziationen
Eine Assoziation zwischen Klassen mit den Namen und wird als Relation zwischen den Mengen der Objekte der Klassen interpretiert, . Die Multiplizitäten müssen in beiden Richtungen wie oben beschrieben behandelt werden. Diese Darstellung erlaubt allerdings keine Behandlung der Rollennamen an den Assoziationsenden. Um dies dennoch zu ermöglichen könnte eine eindeutige Labelfunktion und deren Inverse eingeführt werden.
Bei dieser Art der Betrachtung der Semantik wird nicht zwischen normalen Assoziationen und deren speziellen Ausprägungen (Aggregation, Komposition) unterschieden.
Operationen
Im Allgemeinen löst eine Operation einen Übergang von einer Konfiguration zu einer anderen aus. Im Falle nicht-deterministischer Operationen gibt es eine Menge von Nachfolge-Konfigurationen. Einen Sonderfall stellen Query-Operationen dar. Da diese keine Seiteneffekte haben dürfen, erfolgt auch kein Zustandsübergang in eine andere Konfiguration. Operationen entsprechen in vielen Programmiersprachen Methoden bzw. Funktionen.
Beispieldiagramm
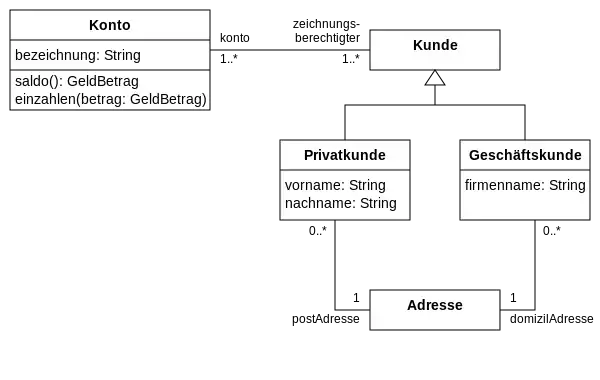
Literatur
- Heide Balzert: Lehrbuch der Objektmodellierung – Analyse und Entwurf mit der UML 2. Elsevier Spektrum Akademischer Verlag, 2005, ISBN 3-8274-1162-9.
- Christoph Kecher: UML 2.0 – Das umfassende Handbuch. Galileo Computing, 2006, ISBN 3-89842-738-2.
- Chris Rupp, Stefan Queins, Barbara Zengler: UML 2 Glasklar. Hanser Verlag, 2007, ISBN 978-3-446-41118-0.
- James Rumbaugh, Ivar Jacobson, Grady Booch: The Unified Modeling Language Reference Manual. Addison-Wesley, 1998, ISBN 978-0-201-30998-0.
Weblinks
Einzelnachweise
- Heide Balzert: Lehrbuch der Objektmodellierung: Analyse und Entwurf mit der UML 2. 2. Auflage. Spektrum Akademischer Verlag, Heidelberg 2005, ISBN 978-3-8274-2903-2, S. 543.
- James Rumbaugh, Ivar Jacobson, Grady Booch: The Unified Modeling Language Reference Manual. Addison-Wesley, 1998, ISBN 978-0-201-30998-0.