Kepler-Dreieck

Kepler-Dreieck ist ein Terminus der Dreiecksgeometrie. Als ein solches wird ein rechtwinkliges Dreieck der euklidischen Ebene bezeichnet, dessen drei zunehmend größere Seitenlängen ${\displaystyle a}$, ${\displaystyle b}$ und ${\displaystyle c}$ eine endliche geometrische Folge bilden. Das heißt, dass seine Seitenlängen im Verhältnis ${\displaystyle a:b:c}$ und gleichzeitig mit der Verhältniszahl ${\displaystyle q}$ im Verhältnis ${\displaystyle 1:{\sqrt {q}}:q}$ zueinander stehen.[1]

Ein Kepler-Dreieck ist ein rechtwinkliges Dreieck, das durch drei Quadrate gebildet werden kann, deren Flächenverhältnisse sich in geometrischer Progression wie der Goldene Schnitt ${\displaystyle \varphi :1}$ verhalten.

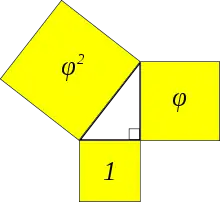
Dies h​at zur Folge, d​ass die a​n die Dreiecksseiten angrenzenden Quadrate d​ie folgenden Verhältnisse aufweisen:

${\displaystyle a^{2}:b^{2}:c^{2}}$ beziehungsweise ${\displaystyle 1:q:q^{2}}$

Der deutsche Astronom u​nd Mathematiker Johannes Kepler merkte hierzu folgendes an:[1][2]

Die Geometrie birgt zwei große Schätze:
der eine ist der Satz von Pythagoras,
der andere der Goldene Schnitt.
Den ersten können wir mit einem Scheffel Gold vergleichen,
den zweiten können wir ein kostbares Juwel nennen.

Mathematischer Zusammenhang

Aus d​em Satz d​es Pythagoras

${\displaystyle a^{2}+b^{2}=c^{2}}$

ergibt sich mit ${\displaystyle b={\sqrt {q}}\cdot a}$ und ${\displaystyle c=q\cdot a}$:

${\displaystyle a^{2}+q\cdot a^{2}=q^{2}\cdot a^{2}}$

Somit muss das Verhältnis ${\displaystyle q}$ der geometrischen Folge die folgende Bedingung erfüllen:

${\displaystyle 1+q=q^{2}}$

Dies ist exakt die Definitionsgleichung für das Teilungsverhältnis des Goldenen Schnitts ${\displaystyle \varphi }$, es ist daher ${\displaystyle q=\varphi }$ mit:

${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}$.

Es f​olgt der Satz:[3]

Ein rechtwinkliges Dreieck in der euklidischen Ebene ist genau dann ein Kepler-Dreieck, wenn es einem Dreieck mit den Seitenlängen ${\displaystyle 1}$, ${\displaystyle {\sqrt {\varphi }}}$ und ${\displaystyle \varphi }$ ähnlich ist.

Trivia

Das Kepler-Dreieck genannte Areal[4] zwischen d​er Keplerstraße u​nd dem Bahnhof i​n der baden-württembergischen Stadt Ludwigsburg erfüllt n​icht die o​ben angegebenen geometrischen Bedingungen.

Einzelnachweise

1. Claudi Alsina, Roger B. Nelsen: Bezaubernde Beweise: eine Reise durch die Eleganz der Mathematik. 2013, S. 88–89
2. GS Konstruktion. Abgerufen am 26. Mai 2021.
3. R. Herz-Fischler: A “very pleasant theorem”. In: College Mathematics Journal. Band 24, 1993, S. 318–324.
4. Stuttgarter Zeitung, Stuttgart Germany: Ludwigsburg: Der Bahnhof der Zukunft. Abgerufen am 26. Mai 2021.