Kaktusgraph
In der Graphentheorie bezeichnet ein Kaktusgraph (zum Teil auch nur Kaktus) einen zusammenhängenden Graphen, in dem sich jedes Paar seiner Kreise höchstens einen gemeinsamen Knoten teilt.[1]
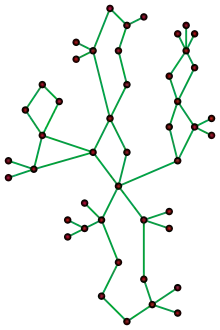
Ein Kaktusgraph
Den Begriff Kaktusgraph (engl. cactus) führten Frank Harary und George Eugene Uhlenbeck ein.[2] In dieser ursprünglichen Definition wurde jedoch verlangt, dass alle Kreise des Graphen Dreiecke sind.
Eigenschaften
- Ein Graph G ist ein Kaktusgraph genau dann, wenn die Anzahl seiner Zyklen seiner zyklomatischen Zahl entspricht.
- Kaktusgraphen sind außerplanare Graphen.
- Jeder planare 3-zusammenhängende Graph besitzt einen aufspannenden Kaktusgraphen, der die Eigenschaft hat, dass das Entfernen eines beliebigen Knoten den Graphen in maximal zwei Zusammenhangskomponenten teilt.[3]
- Die Familie aller Kaktusgraphen kann durch einen verbotenen Minor charakterisiert werden. Dieser Minor entspricht dem vollständigen Graphen in welchem eine Kante entfernt wurde.[4]
Einzelnachweise
- Dennis Geller, Bennet Manvel: Reconstruction of cacti. In: Canad. J. Math.. 21, 1969, S. 1354–1360. doi:10.4153/CJM-1969-149-3.
- Frank Harary, George E. Uhlenbeck: On the number of Husimi trees, I. In: Proceedings of the National Academy of Sciences. 39, Nr. 4, 1953, S. 315–322. Mathematical Reviews 0053893. doi:10.1073/pnas.39.4.315.
- Tom Leighton, Ankur Moitra: Some Results on Greedy Embeddings in Metric Spaces. In: Discrete & Computational Geometry. 44, Nr. 3, 2010, S. 686–705. doi:10.1007/s00454-009-9227-6.
- Ehab El-Mallah, Charles J. Colbourn: The complexity of some edge deletion problems. In: IEEE Transactions on Circuits and Systems. 35, Nr. 3, 1988, S. 354–362. doi:10.1109/31.1748.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.