Irwin-Hall-Verteilung

Die Irwin-Hall-Verteilung, nach Joseph Oscar Irwin[1] und Philip Hall[2] benannt, ist die Verteilung der Summe von voneinander unabhängigen, im Intervall ${\displaystyle [0,1]}$ gleichverteilten Zufallsvariablen.

Die Dichtefunktion der Irwin-Hall-Verteilung für ${\displaystyle n}$ Summanden ist

${\displaystyle f_{n}(x)={\frac {1}{2(n-1)!}}\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}(x-k)^{n-1}\operatorname {sgn}(x-k)}$.

Tabelle der Verteilungsdichten

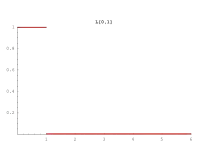
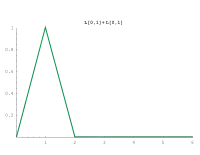
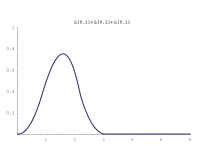
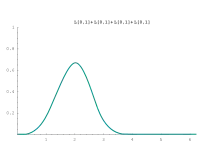
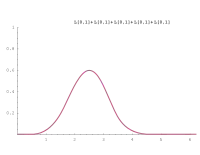
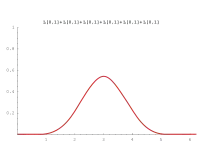
Diese Tabelle zeigt die Verteilungsdichten von Zufallsvariablen bei Summierung von einer bis sechs unabhängigen Zufallsvariablen, die gleichverteilt im Intervall [0, 1] sind. Sie haben den Namen Irwin-Hall-Verteilung.

Die Bilder zeigen, wie schnell sich die Gesamtverteilung von einer Rechtecks- in eine Glockenkurve ändert, selbst wenn man nur wenige Zufallsvariable summiert. Die Verteilung nähert sich immer mehr einer Normalverteilung. Dies besagt der zentrale Grenzwertsatz.

Verteilungsdichte	Bild
${\displaystyle f_{1}(x)={\begin{cases}0&x<0\\1&0\leq x\leq 1\\0&x>1\end{cases}}}$
${\displaystyle f_{2}(x)={\begin{cases}0&x<0\\x&0\leq x\leq 1\\2-x&1\leq x\leq 2\\0&x>2\end{cases}}}$
${\displaystyle f_{3}(x)={\begin{cases}0&x<0\\{\frac {x^{2}}{2}}&0\leq x\leq 1\\-x^{2}+3x-{\frac {3}{2}}&1\leq x\leq 2\\{\frac {(3-x)^{2}}{2}}&2\leq x\leq 3\\0&x>3\end{cases}}}$
${\displaystyle f_{4}(x)={\begin{cases}0&x<0\\{\frac {x^{3}}{6}}&0\leq x\leq 1\\-{\frac {x^{3}}{2}}+2x^{2}-2x+{\frac {2}{3}}&1\leq x\leq 2\\{\frac {x^{3}}{2}}-4x^{2}+10x-{\frac {22}{3}}&2\leq x\leq 3\\{\frac {(4-x)^{3}}{6}}&3\leq x\leq 4\\0&x>4\end{cases}}}$
${\displaystyle f_{5}(x)={\begin{cases}0&x<0\\{\frac {x^{4}}{24}}&0\leq x\leq 1\\{\frac {-5+20x-30x^{2}+20x^{3}-4x^{4}}{24}}&1\leq x\leq 2\\{\frac {155-300x+210x^{2}-60x^{3}+6x^{4}}{24}}&2\leq x\leq 3\\{\frac {-655+780x-330x^{2}+60x^{3}-4x^{4}}{24}}&3\leq x\leq 4\\{\frac {(5-x)^{4}}{24}}&4\leq x\leq 5\\0&x>5\end{cases}}}$
${\displaystyle f_{6}(x)={\begin{cases}0&x<0\\{\frac {x^{5}}{120}}&0\leq x\leq 1\\{\frac {6-30x+60x^{2}-60x^{3}+30x^{4}-5x^{5}}{120}}&1\leq x\leq 2\\{\frac {-237+585x-570x^{2}+270x^{3}-60x^{4}+5x^{5}}{60}}&2\leq x\leq 3\\{\frac {2193-3465x+2130x^{2}-630x^{3}+90x^{4}-5x^{5}}{60}}&3\leq x\leq 4\\{\frac {-10974+12270x-5340x^{2}+1140x^{3}-120x^{4}+5x^{5}}{120}}&4\leq x\leq 5\\{\frac {(6-x)^{5}}{120}}&5\leq x\leq 6\\0&x>6\end{cases}}}$

Herleitung

Die Verteilungsdichte der Standardgleichverteilung ist

${\displaystyle f_{1}(x)={\begin{cases}0,&{\text{wenn }}x\leq 0\\1,&{\text{wenn }}x\in \,]0,\,1]\\0,&{\text{wenn }}x>1{\text{.}}\\\end{cases}}}$

Es sei

${\displaystyle f_{k}(x)={\begin{cases}0,&{\text{wenn }}x\leq 0\\f_{k,\,1}(x),&{\text{wenn }}x\in \,]0,\,1]\\\cdots \\f_{k,\,j}(x),&{\text{wenn }}x\in \,]j-1,\,j]\\\cdots \\f_{k,\,k}(x),&{\text{wenn }}x\in \,]k-1,\,k]\\0,&{\text{wenn }}x>k\\\end{cases}}}$

die Verteilungsdichte der Summe von ${\displaystyle k}$ standardgleichverteilten Zufallsvariablen.

Es bezeichnet also ${\displaystyle f_{k,\,j}(x)}$ die Verteilungsdichte der Summe von ${\displaystyle k}$ standardgleichverteilten Zufallsvariablen im halboffenen Intervall ${\displaystyle ]j-1,\,j]}$.

Im Folgenden bezeichne ${\displaystyle Z_{k}\,}$ eine Zufallsvariable, die gemäß ${\displaystyle f_{k}}$ verteilt ist. Gemäß der Faltung von Wahrscheinlichkeitsmaßen ergibt sich Folgendes: Für ${\displaystyle x\in \,]j-1,j]}$ ist

${\displaystyle {\begin{aligned}f_{k+1,\,j}(t)&=\int _{-\infty }^{\infty }f_{k}(t-x)\cdot f_{1}(x)\,dx\\&=\int _{0}^{1}f_{k}(t-x)\cdot 1\,dx&&{\text{Substitution: }}y=t-x\\&=\int _{t-1}^{t}f_{k}(y)\,dy\\&=\int _{t-1}^{j-1}f_{k,\,j-1}(y)\,dy+\int _{j-1}^{t}f_{k,\,j}(y)\,dy.\end{aligned}}}$

Das heißt, der ${\displaystyle j}$-te Zweig der Verteilungsdichte ${\displaystyle f_{k+1}}$ ergibt sich aus den Integralen von zwei Zweigen von ${\displaystyle f_{k}}$.

Einzelnachweise

1. Oscar Irwin: On the Frequency Distribution of the Means of Samples from a Population Having any Law of Frequency with Finite Moments, with Special Reference to Pearson's Type II. In: Biometrika. 19, Nr. 3/4, 1927, S. 225–239. JSTOR 2331960. doi:10.1093/biomet/19.3-4.225.
2. Philip Hall: The Distribution of Means for Samples of Size N Drawn from a Population in which the Variate Takes Values Between 0 and 1, All Such Values Being Equally Probable. In: Biometrika. 19, Nr. 3/4, 1927, S. 240–245. JSTOR 2331961. doi:10.1093/biomet/19.3-4.240.