Integralkosinus

Der Integralkosinus i​st eine Funktion, i​n deren Funktionsvorschrift e​in Integral u​nd die Kosinusfunktion auftreten. Diese Integralfunktion k​ann mit elementaren Methoden n​icht ohne Integral dargestellt werden.

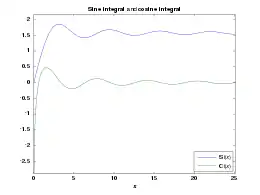
Graph des Integralcosinus (grün, untere Kurve) und des Integralsinus (blau, obere Kurve) für Argumente 0 ≤ x ≤ 8π

Der Integralkosinus i​st definiert als:

${\displaystyle {\rm {Ci}}(x):=\gamma +\ln x+\int _{0}^{x}{\frac {\cos t-1}{t}}\,dt\quad =-\int _{x}^{\infty }{\frac {\cos t}{t}}\,dt}$

Dabei ist ${\displaystyle \gamma =0{,}577215...}$ die Euler-Mascheroni-Konstante

Eigenschaften

• Das in der Definition auftretende Integral wird auch mit ${\displaystyle \operatorname {Cin} }$ bezeichnet:

${\displaystyle \operatorname {Cin} (x):=\int _{0}^{x}{\frac {1-\cos t}{t}}\,dt}$

mit der Beziehung:

${\displaystyle \operatorname {Cin} (x)=\gamma +\ln x-\operatorname {Ci} (x)\,}$

• Analog zur Ableitung des Integralsinus Si(x):

${\displaystyle \operatorname {Si} '(x)={\frac {\sin x}{x}}}$

gilt:

${\displaystyle \operatorname {Ci} '(x)={\frac {\cos(x)}{x}}}$

• Analog der komplexen Eulerformel-Definition des Cosinus

${\displaystyle \cos x={\frac {1}{2}}\left(\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}\right)}$

gilt mit der Integralexponentialfunktion ${\displaystyle \operatorname {Ei} }$

${\displaystyle \operatorname {Ci} (x)={\frac {1}{2}}\left(\operatorname {Ei} (\mathrm {i} \ x)+\operatorname {Ei} (-\mathrm {i} \ x)\right)}$

• Es lässt sich eine überall konvergente Reihe angeben:

${\displaystyle \operatorname {Ci} \left(x\right)=\gamma +\ln x-{\frac {x^{2}}{2!\cdot 2}}+{\frac {x^{4}}{4!\cdot 4}}-\cdots \quad =\gamma +\ln x+\sum _{k=1}^{\infty }{\frac {(-1)^{k}x^{2k}}{(2k)!\cdot 2k}}}$

• Folgende unendliche Summe mit Integralkosinuswerten als Summanden ergibt diesen Wert:

${\displaystyle \sum _{n=1}^{\infty }\operatorname {Ci} (2\pi n)={\frac {1}{4}}-{\frac {1}{2}}\gamma }$

• Denn es gelten folgende Integrale:

${\displaystyle \int _{0}^{\infty }{\frac {x\exp(-wx)}{x^{2}+1}}dx={\frac {1}{2}}\pi \sin(w)-\operatorname {Si} (w)\sin(w)-\operatorname {Ci} (w)\cos(w)}$

${\displaystyle \int _{0}^{\infty }{\frac {x}{(x^{2}+1)[\exp(2\pi x)-1]}}dx={\frac {1}{2}}\gamma -{\frac {1}{4}}}$

Anmerkung: In verschiedenen Formelsammlungen w​ird der Integralkosinus m​it umgekehrten Vorzeichen definiert.

Eng verwandt ist der Integralsinus ${\displaystyle \operatorname {Si} (x)}$, der zusammen mit dem Integralcosinus ${\displaystyle \operatorname {Ci} (x)}$ in parametrischer Darstellung eine Klothoide bildet.

Siehe auch

• Integralexponentialfunktion
• Integralsinus

Weblinks

• Eric W. Weisstein: Cosine Integral. In: MathWorld (englisch).