Hierarchieproblem
Hierarchieproblem ist ein Begriff der Hochenergiephysik, welcher oft speziell in Bezug auf den Wert der Higgsmasse angewendet wird. Es bezeichnet insbesondere das Erklärungsdefizit einer Theorie bezüglich einer deutlichen Differenz zwischen einem fundamentalen Parameter der Theorie (Kopplungskonstante oder Masse) und seinem experimentell bestimmten (oder auch erwarteten) Wert. Es ist verwandt mit dem Natürlichkeitsproblem und dem Feinabstimmungsproblem (fine tuning).
Higgsmasse
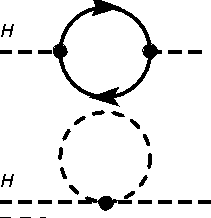
Das prominenteste Hierarchieproblem der Elementarteilchenphysik ist die Frage, weshalb die Gravitation deutlich schwächer ist als die elektroschwache Wechselwirkung. Technisch drückt sich dies in der Größe der Higgsmasse aus, welche die Energieskala der elektroschwachen Wechselwirkung über die Massen der Eichbosonen festlegt (Higgs-Mechanismus). Im Rahmen einer Quantenfeldtheorie sind dabei Strahlungs- und Schleifenkorrekturen (Feynman-Graphen höherer Ordnung) der Masse eines Teilchens zu beachten (effektive Masse, siehe auch Selbstenergie). Diese Korrekturen können die „eigentliche“, nackte Masse (bare mass) des Teilchens deutlich übersteigen, sodass die effektive Masse abweicht. Während die Massen der Eichbosonen vor solchen Korrekturen durch lokale Eichsymmetrien und die Fermionen durch chirale Symmetrie geschützt sind, ist dies beim skalaren (Spin 0) Higgs-Boson nicht möglich.
Skalare können nicht durch eine Symmetrie vor immensen Strahlungskorrekturen durch Kopplung an andere Teilchen bewahrt werden, ihre Masse divergiert aufgrund solcher Korrekturen quadratisch mit der höchsten Energieskala der Theorie. Man erwartet deshalb für Skalare eine natürliche Masse von der Größenordnung dieser Skala. Bei einer Quantenfeldtheorie, die auch die Gravitation einbezieht, ist dies die Planck-Skala. Jedoch liegt die Planck-Skala (Größenordnung 1019 GeV) 16 Größenordnungen über der elektroschwachen Skala (Größenordnung 103 GeV). Die effektive (also experimentell zugängliche) Higgsmasse, deren Wert man für den Higgs-Mechanismus im Bereich der elektroschwachen Skala benötigt und der inzwischen experimentell zu etwa 125 GeV bestimmt wurde, ist also nicht bei ihrem natürlichen Wert in der Nähe der Planck-Masse (Natürlichkeitsproblem).
Zwar kann diese quadratische Divergenz wegrenormiert und die Higgsmasse so auf ihren gewünschten Wert in der Nähe der elektroschwachen Skala gebracht werden, dies erfordert jedoch technisch anspruchsvolles und unnatürliches fine-tuning. Außerdem bleibt der Ursprung der Higgsmasse so ohne Weiteres unverstanden.
Darüber hinaus erhält man bei der Berechnung der Higgsmasse aus den Feynmangraphen höherer Ordnung zusätzlich eine endliche Korrektur, die von den Massen und Kopplungskonstanten der übrigen Teilchen der Theorie abhängt. Für die Teilchen des Standardmodells sind die daraus resultierenden Korrekturen vernachlässigbar, sie werden allerdings groß für möglicherweise existierende sehr schwere Teilchen, selbst wenn das Higgs nur sehr indirekt an diese koppelt. Auch wenn das Higgs-Boson zentraler Bestandteil des Standardmodells der Elementarteilchenphysik ist, ist das Hierarchieproblem somit kein Problem des Standardmodells selbst, da es keine dieser schweren Teilchen enthält. Streng genommen kann das Hierarchieproblem innerhalb des Standardmodells nicht einmal formuliert werden, da eine Berechnung der Higgsmasse dort nicht möglich ist. Das Problem ist vielmehr, dass die Higgsmasse sehr sensitiv auf neue Physik („beyond the Standard Model“) ist.
Somit ist die Brisanz des Hierarchieproblems darauf zurückzuführen, dass das Standardmodell der Elementarteilchenphysik zwar eine in sich konsistente Theorie ist und mit den bisherigen experimentellen Daten sehr gut übereinstimmt, es aber vor allem aus theoretischer Sicht einige Gründe gibt, anzunehmen, dass es sich beim Standardmodell nicht um die letztgültige Theorie handelt und man in höheren Energiebereichen neue Physik erwartet.
So widerspricht dem Standardmodell zwar aktuell kein experimenteller Befund (allerdings widersprechen die Hinweise auf minimale, aber nicht verschwindende Neutrinomassen der Annahme des Standardmodells), jedoch wurde es bisher auch nur in einem Energiebereich unterhalb der TeV-Skala im großen Stil getestet. Ferner werden zwar die elektromagnetische und die schwache Wechselwirkung innerhalb des Standardmodells zur elektroschwachen Wechselwirkung vereinigt, jedoch ist eine Vereinigung mit der starken Wechselwirkung (GUT) oder gar der Gravitation im Standardmodell nicht möglich. Auch in Bezug auf die Anzahl der Parameter (etwa 20) ist das Standardmodell aus theoretischer Sicht unbefriedigend. Darüber hinaus scheinen Hinweise auf Dunkle Materie oder Dunkle Energie nicht im Rahmen der Standardmodelle der Teilchenphysik und Kosmologie erklärbar zu sein und auf neue Physik „beyond Standard Model“ (z. B. die erwähnten neuen schweren Teilchen) zu deuten.
- „Based only on a proper respect for the power of Nature to surprise us, it seems nearly as obvious that new physics exists in the 16 orders of magnitude in energy between the presently explored territory near the electroweak scale and the Planck scale.“ – Stephen P. Martin: A Supersymmetry Primer[1]
- („Allein auf Grund eines angemessenen Respekts für die Kraft der Natur uns zu überraschen, erscheint es nahezu selbstverständlich, dass in den 16 Energie-Größenordnungen zwischen dem bisher erforschten Bereich nahe der elektroschwachen Skala und der Planck-Skala neue Physik existiert.“)
Lösungsvorschläge
Supersymmetrie
Ein Ausweg aus dem Hierarchieproblem ist die Supersymmetrie (SUSY). Da Bosonen und Fermionen mit unterschiedlichen Vorzeichen zu den Korrekturen beitragen, ist es naheliegend (wenn auch nicht die historische Motivation) zur Lösung des Hierarchieproblems eine Bosonen-Fermionen-Symmetrie einzuführen. Im Falle exakter Supersymmetrie heben sich die problematischen Terme dann automatisch gegenseitig auf, ein fine tuning ist also nicht nötig. Selbst wenn Supersymmetrie gebrochen ist (was in der Tat der Fall sein muss, wenn sie existiert), wenn sie also nicht exakt ist, ergeben sich maximal logarithmisch divergente Terme, welche unproblematisch sind. Damit diese Divergenzen und damit die Higgsmasse nicht zu groß werden, ist SUSY auf einen Energiebereich von wenigen TeV eingeschränkt.
Stringtheorie
Eine weitere Lösung bietet die Stringtheorie, in der bis zu zehn kompaktifizierte Extradimensionen vorkommen, die einen Radius von bis zu einem Zehntel Millimeter besitzen können und in die nur die Gravitation vorzudringen vermag. In diesen Extradimensionen würde die Gravitationskraft erheblich abgeschwächt. Die eigentliche Kraft wäre in Wirklichkeit also viel größer und würde sich den anderen drei Grundkräften annähern.
Randall-Sundrum-Modell
Einen dritten Lösungsansatz für das Problem bietet das Randall-Sundrum-Modell. Dieses versucht das Hierarchieproblem durch die Einführung einer einzigen weiteren Dimension zu lösen – das unterscheidet das Modell von den String-Theorien.
Literatur
- Lisa Randall – Warped Passages. Unraveling the Mysteries of the Universe's Hidden Dimensions, New York 2005; ISBN 0-06-053108-8 (auf deutsch erschienen im Oktober 2006 unter dem Titel: Verborgene Universen. Eine Reise in den extradimensionalen Raum, S. Fischer Verlag, ISBN 3-10-062805-5)
- G. F. Giudice, Odyssee im Zeptoraum: Eine Reise in die Physik des LHC, Springer-Verlag, Berlin Heidelberg 2012, ISBN 978-3-642-22394-5.