Heaviside-Bedingung

Die Heaviside-Bedingung, benannt nach Oliver Heaviside, ist eine Bedingung, der eine elektrische Leitung im Rahmen der Leitungstheorie genügen muss, damit keine Verzerrungen des zu übertragenden Signals auftreten. Die Erfüllung dieser Bedingung kann bei Übertragungsleitungen durch die Steigerung der Induktivität der Leitung erfolgen, wie es beispielsweise historisch durch die sogenannte bespulte Leitung erreicht wurde.

Definition

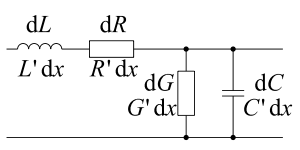
Ersatzschaltbild für ein Leitungselement einer Zweidrahtleitung der infinitesimalen Länge dx.

Eine Übertragungsleitung kann im Ersatzschaltbild als eine Summe von Leitungsabschnitten der infinitesimalen Länge $dx$ , wie in nebenstehender Abbildung, dargestellt werden. Die elektrischen Eigenschaften dieses Leiters sind, bezogen auf $dx$ : Der Induktivitätsbelag L′, der Kapazitätsbelag C′, der Widerstandsbelag R′ und der Ableitungsbelag G′.

Für eine ideale verlustlose Leitung gilt $R'=0$ und $G'=0$ .

Bei einer realen Leitung sorgen hingegen der Widerstandsbelag $R'\neq 0$ und der Ableitungsbelag $G'\neq 0$ für Verluste und Verzerrungen auf der Leitung. Praktisch gilt dabei immer

{\frac {G'}{C'}}\ll {\frac {R'}{L'}}

Ist allerdings die Heaviside-Bedingung

{\frac {G'}{C'}}={\frac {R'}{L'}}

erfüllt, dann erfolgt die Übertragung verzerrungsfrei. Außerdem zeigt sich, dass in diesem Fall (bei gleichbleibendem Widerstandsbelag und Ableitungsbelag) die Verluste auf der Leitung minimal sind. Die dafür nötige Erhöhung von L′ wurde früher durch Pupin-Spulen erreicht.

Hintergrund

Das zu übertragende Signal kann auch auf einer linearen Übertragungsleitung verzerrt werden. Die Phasengeschwindigkeit der Frequenzanteile des Signals ist durch ihre nichtlinear von der Frequenz abhängige Phasenkonstante selbst frequenzabhängig. Wenn verschiedene Frequenzanteile bei verschiedenen Geschwindigkeiten übertragen werden, „verschmiert“ das Signal (Dispersion). Außerdem kann die Dämpfung der Leitung mit der Frequenz variieren (z. B. durch den Skineffekt), so dass die Signalform verändert wird.

Dies war ein großes Problem bei den ersten transatlantischen Fernmeldekabeln, das durch Untersuchungen von Lord Kelvin zu der Problematik der Dispersion führte und schließlich von Heaviside, der sich Maßnahmen dagegen überlegte, gelöst wurde. Bei sehr großer Dispersion können sich aufeinanderfolgende Impulse überschneiden und zu Symbolübersprechen führen. Um dies zu verhindern, musste die Schrittgeschwindigkeit auf 1/15 Baud reduziert werden. Dies ist sogar für die Morse-Übertragung sehr langsam.

Herleitung

In der Leitungstheorie wird mit Hilfe der komplexen Wechselstromrechnung gezeigt, dass für das Verhältnis der komplexen Amplitude einer sinusförmigen Spannungswelle $U(x)$ zwischen zwei Punkten einer Übertragungsleitung mit dem Abstand $\Delta x$ unter Ausschluss von Reflexionen gilt

{\frac {U(x+\Delta x)}{U(x)}}=e^{-\gamma \Delta x}

Deshalb werden die Eigenschaften der Wellenausbreitung ausschließlich bestimmt von der Fortpflanzungskonstante

\gamma =\alpha +j\beta ={\sqrt {(R'+j\omega L')(G'+j\omega C')}}

wobei der Realteil α als Dämpfungskonstante und der Imaginärteil β als Phasenkonstante bezeichnet werden.

Soll die Welle verzerrungsfrei übertragen werden, dann darf α nicht von der Kreisfrequenz ω abhängig sein, während β zu ω proportional sein muss. Letzteres bedeutet, dass die Phasengeschwindigkeit

v_{ph}={\frac {\omega }{\beta }}

über alle Frequenzen konstant ist.

Das Quadrat der Fortpflanzungskonstanten

\gamma ^{2}=(\alpha +j\beta )^{2}=(R'+j\omega L')(G'+j\omega C')\,

muss bei Verzerrungsfreiheit die Form $(A+j\omega B)^{2}$ ergeben. Dies ist nur der Fall, wenn sich $(R'+j\omega L')$ und $(G'+j\omega C')$ nicht um mehr als einen konstanten Faktor unterscheiden. Da beide einen Real- und Imaginärteil besitzen, müssen sich diese durch den gleichen Faktor unterscheiden, so dass gilt

{\frac {R'}{G'}}={\frac {j\omega L'}{j\omega C'}}={\frac {L'}{C'}}

was gerade die Heaviside-Bedingung ist.

Eigenschaften der verzerrungsfreien Leitung

Eine Übertragungsleitung, welche die Heaviside-Bedingung erfüllt, hat die folgenden charakteristischen Merkmale:

Dämpfung

Die Dämpfung hat den frequenzunabhängigen Wert der Gleichstromdämpfung:

\alpha ={\sqrt {R'G'}}

Insbesondere kann man zeigen, dass diese bei erfüllter Heaviside-Bedingung minimal bezüglich der Variation von Kapazitäts- oder Induktivitätsbelag wird, was ebensolche praktische Bedeutung wie die Verzerrungsfreiheit hat.

Phasenkonstante

Die Phasenkonstante wächst linear mit der Frequenz und entspricht der der verlustlosen Leitung:

\beta =\omega {\sqrt {L'C'}}

Phasengeschwindigkeit

Die Phasengeschwindigkeit ist konstant und entspricht der der verlustlosen Leitung:

v_{ph}={\frac {\omega }{\beta }}={\frac {1}{\sqrt {L'C'}}}

Deshalb unterscheidet sie sich nicht von der Gruppengeschwindigkeit:

v_{g}={\frac {d\omega }{d\beta }}={\frac {1}{\sqrt {L'C'}}}

Leitungswellenwiderstand

Die Leitungswellenwiderstand einer verlustbehafteten Übertragungsleitung ist gegeben durch

Z_{l}={\sqrt {\frac {R'+j\omega L'}{G'+j\omega C'}}}

Es ist allgemein nicht möglich, die Übertragungsleitung über alle Frequenzen genau anzupassen, da durch die Wurzel die Funktion des Wellenwiderstandes irrational von der Frequenz abhängig ist, so dass sie nicht als Netzwerk aus diskreten Bauelementen dargestellt werden kann. Wenn eine Leitung aber die Heaviside-Bedingung erfüllt, dann wird der Wellenwiderstand frequenzunabhängig und rein reell. Er entspricht sowohl dem der verlustlosen Leitung als auch dem bei Gleichstrom:

Z_{l}={\sqrt {\frac {L'}{C'}}}={\sqrt {\frac {R'}{G'}}}

Eine solche Leitung kann dann reflexionsfrei angepasst werden, indem sie nur mit ohmschen Widerständen an den Enden abgeschlossen wird.

Literatur

K. Küpfmüller und G. Kohn: Theoretische Elektrotechnik und Elektronik, Eine Einführung. 16. Auflage. Springer, 2005, ISBN 3-540-20792-9.
Eugen Philippow: Grundlagen der Elektrotechnik. Akademische Verlagsgesellschaft Geest&Portig K.-G., Leipzig 1967.

Siehe auch

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.