HDRI-Erzeugung aus Belichtungsreihen
In der Digitalfotografie kann ein HDR-Bild mit hohem Helligkeitsumfang aus einer Belichtungsreihe von herkömmlichen Bildern mit geringem Helligkeitsumfang (LDR-Bildern) erzeugt werden. Da heutige HDR-Bildsensoren und -Kameras sehr teuer sind, ist diese Technik in Verbindung mit herkömmlichen Digitalkameras das Mittel der Wahl, um kostengünstig HDR-Bilder zu erzeugen.
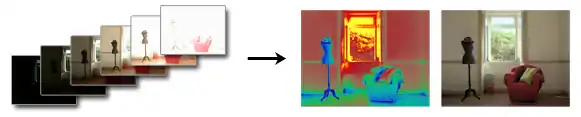
Prinzip
Wenn eine Szene mehrmals mit unterschiedlichen Belichtungszeiten aufgenommen wurde, enthält jedes Bild unterschiedliche Pixel, die über- oder unterbelichtet wurden. Zur Erzeugung eines HDR-Bildes wird davon ausgegangen, dass die Helligkeit und Farbe der meisten Pixel in mindestens einem Bild der Serie korrekt wiedergegeben werden.
Unter der Annahme, dass die Kamera auf Helligkeit linear anspricht, kann jedes Einzelbild auf die gleiche Helligkeitseinheit gebracht werden, indem man dessen Pixelwerte durch die Belichtungszeit teilt. Anschließend kann ein HDR-Bild erzeugt werden, indem der Mittelwert der Einzelbilder unter Ausschluss der über- und unterbelichteten Pixel berechnet wird. Die Umwandlung des so erzeugten HDR-Bildes in ein LDR-Bild zur Anzeige auf herkömmlichen Bildschirmen geschieht mittels Tone Mapping.
In der Praxis weisen Digitalkameras kein lineares Ansprechverhalten auf, sondern sind durch eine „Kamerakurve“ (opto-elektronische Übertragungsfunktion auch opto-electronic conversion function oder OECF) charakterisiert, die angibt, wie die Kamera auf unterschiedliche Helligkeiten reagiert. Außerdem stehen meist weder die Kamera noch die abgebildeten Objekte völlig still. Hinzu kommt, dass die Kameraoptik einen Teil des Lichts streut, was zu unerwünschten Lens-Flare-Effekten führt, die korrigiert werden müssen. Auch aus unterschiedlich lange belichteten und entwickelten Negativfilmen kann ein HDR-Bild erzeugt werden, wobei hier einige dieser Probleme nicht auftreten (siehe auch Multi-Exposure), andere verändert wirken und bei der Aufnahme kalkuliert werden müssen, im analogen etwa der Schwarzschildfaktor sowie der Farbkorrektur.

 f/4 – 1 Sek.
f/4 – 1 Sek. f/4 – 1/4 Sek.
f/4 – 1/4 Sek. f/4 – 1/8 Sek.
f/4 – 1/8 Sek. f/4 – 1/15 Sek.
f/4 – 1/15 Sek. f/4 – 1/30 Sek.
f/4 – 1/30 Sek.
Technik
Gewichtung der Pixel
Bei der Kombination der Einzelbilder zu einem HDR-Bild müssen zwar die über- und unterbelichteten Pixel ignoriert werden, dies lässt jedoch die Frage offen, wie die Pixel mit dazwischen liegender Helligkeit im Verhältnis zu den Pixeln der anderen Einzelbilder gewichtet werden sollen. Hierzu wurden verschiedene Methoden vorgeschlagen.
Mann und Picard gingen davon aus, dass eine höhere Empfindlichkeit beim Ansprechverhalten des Bildsensors zu einem zuverlässigeren Helligkeitswert führt, und schlugen deshalb als Gewichtungsfunktion die Ableitung der Kamerakurve vor.[1] Debevec und Malik hingegen vermieden die großen Steigungen der Kamerakurve bei sehr niedrigen und hohen Helligkeitswerten und nutzten zur Gewichtung eine zu den Extremen abfallende Funktion, die Pixel mit mittlerem Helligkeitswert bevorzugt behandelt.[2] Mitsunaga und Nayar legten anhand von signaltheoretischen Argumenten dar, dass höhere Werte weniger anfällig für Rauschen sind, und multiplizierten daher Mann und Picards Funktion mit dem Pixelwert.[3] Mitsunaga und Nayars Gewichtungsfunktion kann mit Debevec und Maliks Funktion multipliziert werden, um zweifelhafte Intensitätswerte nahe den Extremen zu vermeiden.[4]
Positionsangleichung
Da die Kamera bei der Aufnahme der Einzelbilder selbst bei Nutzung eines Stativs oft wackelt, kommt es beim Zusammenführen der Einzelbilder zu Unschärfe, sofern ihre Position nicht vorher angeglichen wird. Zwar wurden vor allem im Bereich des maschinellen Sehens diverse Techniken entwickelt, um mehrere Bilder anzugleichen, doch nur wenige befassen sich speziell mit dem Problem der HDR-Erzeugung.
Motion Estimation
Kang et al. lösen das Problem der Positionsangleichung durch eine Variante des Motion-Estimation-Algorithmus von Lucas und Kanade (siehe Lucas-Kanade-Methode).[5][6] Für jedes Pixel zwischen zwei aufeinanderfolgenden Einzelbildern wird ein Bewegungsvektor ermittelt, der anschließend korrigiert wird. Sobald für jedes Pixel der Bewegungsvektor ermittelt ist, werden aufeinanderfolgende Einzelbilder verformt und können zusammengeführt werden.
Vorteilhaft an diesem Verfahren ist, dass größere Bewegungen sowohl der Kamera als auch der Objekte kompensiert werden. Daher eignet es sich zur Aufnahme von HDR-Videos, wobei mehrere unterschiedlich belichtete Aufnahmen zu je einem HDR-Einzelbild des Videos zusammengefasst werden. Ein Nachteil des Verfahrens ist, dass zu seiner Anwendung die Kamerakurve bekannt sein muss.[7]
Weitere Methoden zur Positionsangleichung, die Änderungen der Perspektive oder Rotationen korrigieren können, wurden von Candocia[8] sowie Kim und Polleyfeys[9] entwickelt.
Schwellenwert-Bitmap
Eine einfache und schnelle Technik, die ohne die Kamerakurve auskommt, verwendet eine so genannte Schwellenwert-Bitmap (Mean Threshold Bitmap).[10] Hierbei werden aus den Einzelbildern Schwarzweißbilder erzeugt, deren Verschiebung relativ zu einem willkürlich bestimmten Referenzbild sich leicht berechnen lässt.
Dazu wird jedes Einzelbild zunächst in ein Graustufenbild umgewandelt. Anschließend wird daraus eine Schwellenwert-Bitmap berechnet, wobei der Median der Helligkeit als Schwellenwert genommen wird. Bei sehr hellen oder dunklen Bildern werden andere Schwellenwerte verwendet, um exzessives Rauschen zu vermeiden. Im Gegensatz zu Kantendetektionsfiltern bieten Schwellenwert-Bitmaps auch bei unterschiedlichen Belichtungszeiten ein konsistentes Abbild der aufgenommenen Szene.
Zusätzlich werden aus um Zweierpotenz-Faktoren verkleinerten Versionen des Graustufenbilds weitere Bitmaps auf die gleiche Weise berechnet. Ausgehend von den jeweils kleinsten Bildversionen wird die XOR-Differenz zur Referenzbitmap berechnet, wobei die Bitmap um ±1 Pixel in der X- und Y-Achse verschoben werden kann. Bildbereiche, deren Graustufenwert nahe am Schwellenwert lag, werden dabei ignoriert, da sie in der Bitmap oft verrauscht sind. Dies wiederholt sich für jede nächstgrößere Bildversion, wobei die Verschiebungen jeweils zusätzlich zu der Position erfolgen, die im vorhergehenden Schritt die kleinste XOR-Differenz ergeben hat. Am Ende kann so die Position des Bildes relativ zum Referenzbild ermittelt werden.
Die Schwellenwert-Technik hilft nur gegen Verwacklungen und ist nicht bei einzelnen bewegten Objekten und größeren Zooms oder Rotationen der Kamera anwendbar.
Auswertung der Kamerakurve
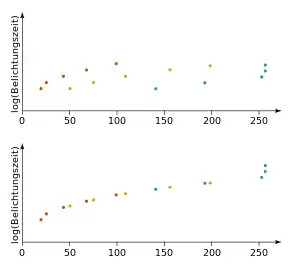
Auf die Pixelwerte der Einzelbilder muss vor ihrer Zusammenführung zu einem HDR-Bild die Umkehrfunktion der Kamerakurve angewandt werden, um lineare Helligkeitswerte zu erhalten. Diese Funktion wird im Allgemeinen nicht von den Kameraherstellern veröffentlicht. Eine sRGB-Tonwertkurve ist keine brauchbare Annahme, da die meisten Hersteller den Farbkontrast über die sRGB-Kurve hinaus erhöhen, um ein lebendiger wirkendes Bild zu erhalten. Außerdem wird die Kurve oft zu den Extremen hin verändert, um weichere Glanzlichter und weniger sichtbares Rauschen in dunklen Bereichen zu erhalten.[11] Falls das Verhalten der Kamera sich nicht in Abhängigkeit von der Belichtungszeit ändert, ist es möglich, die Kamerakurve aus einer Bilderserie mit unterschiedlichen Belichtungszeiten zu ermitteln. Es wird dabei empfohlen, die Funktion nur einmal anhand einer Szene mit vielen neutralen Grautönen festzustellen und anschließend für alle Szenen wiederzuverwenden.[12]
Die unterschiedlichen Werte, die jeder Punkt des Bildes in Abhängigkeit von der Belichtungszeit annimmt, stellen eine Annäherung an die Kamerakurve dar. Da die Belichtungszeiten der Einzelbilder bekannt sind, kann die Kurve rekonstruiert werden. Das nebenstehende Bild zeigt die Kamerakurve, die an drei unterschiedlichen Bildpositionen mit jeweils fünf unterschiedlichen Belichtungszeiten ausgewertet wurde. Zwar lässt sich so die Form der Kurve in jedem Bereich ermitteln, nicht jedoch, wie die einzelnen Kurvenabschnitte miteinander verbunden sind. Debevec und Malik lösen dieses Problem durch lineare Optimierung, also durch Berechnung der Parameter einer Zielfunktion, die die mittlere quadratische Abweichung zu den Punkten minimieren.[2] Dabei werden die drei RGB-Farbkanäle unabhängig voneinander behandelt. Ein etwas aufwändigeres Verfahren wurde von Mitsunaga und Nayar veröffentlicht.[3] Die Zielfunktion berücksichtigt hierbei auch variable Verhältnisse aufeinanderfolgender Belichtungszeiten. Dies erlaubt es, die Kamerakurve auch bei preisgünstigen Digitalkameras, bei denen die Blendenzahl und Belichtungszeit nicht genau bekannt sind, angenähert zu rekonstruieren.
Diese Techniken nutzen eine Reihe von Bildpositionen, die den gesamten Helligkeitsbereich möglichst gut abdecken. Zwar wäre es möglich, alle Pixel des Bildes zu verwenden, dies wäre jedoch ineffizient und würde durch Bildrauschen zu Instabilitäten führen. Stattdessen wird vorgezogen, eine Reihe von kleinen Bildregionen mit jeweils annähernd gleicher Helligkeit strategisch auszuwählen (Reinhard u. a. geben als Richtwert 50 Regionen von je 12×12 Pixel an[13]). Dazu wird vom Bild mit geringster Belichtungszeit ausgegangen. Für jedes Bild wird bestimmt, wie viele Regionen des vorhergehenden Bildes noch gültig sind, und wie viele neu gewählt werden müssen. Anschließend werden die benötigten neuen Regionen zufällig ausgewählt, wobei sichergestellt wird, dass sie heller als alle vorhergehenden sind, keine bereits vorhandenen Regionen überlappen und sich im für die aktuelle Belichtungszeit gültigen Helligkeitsbereich befinden.
Handhabung bewegter Objekte
Wenn sich während der Aufnahme der Einzelbilder Objekte oder Personen in der Szene bewegt haben, so erscheinen sie im kombinierten HDR-Bild verschwommen. Die Motion-Estimation-Technik von Lucas und Kanade[6] versucht, dieses Problem durch Verformung von Bildregionen zu lösen, kann aber leere Bildregionen hinterlassen und ist bei komplexen Bewegungen machtlos. Eine andere Möglichkeit besteht darin, für diejenigen Regionen, in denen sich der Bildinhalt ändert, nur jeweils ein Einzelbild auszuwählen; die HDR-Eigenschaften gehen dann in diesen Regionen verloren. Diese Methode liefert nur dann brauchbare Ergebnisse, wenn in den betreffenden Regionen die Helligkeit annähernd einheitlich ist.
Um die Bildregionen mit Bewegungsanteil automatisch zu erkennen, kann für jedes Pixel die gewichtete Varianz aller Einzelbilder berechnet werden.[14] In diesem Varianzbild werden per Floodfill ein „Hintergrundbild“ mit niedriger Varianz sowie zusammenhängende Regionen mit hoher Varianz ermittelt. Das für eine Region zu wählende Einzelbild ist dasjenige, das die hellsten in der Region vorkommenden Bereiche bei möglichst hoher Belichtungszeit enthält. Damit Bereiche mit niedriger Varianz innerhalb einer Region bestehen bleiben, wird zwischen dem originalen HDR-Bild und dem gewählten Einzelbild je nach Varianz eines Pixels interpoliert. Das Ergebnis ist oft nicht perfekt, da Artefakte wie fehlende Objektteile auftreten können.
Filterung der Linsenstreuung
Die meisten Digitalkameras enthalten eine Optik, die für LDR-Bilder ausgelegt wurde. Selbst unter Verwendung hochwertiger Kameras treten diese Beschränkungen in Form der Linsenstreuung (Lens Flare) zutage. Die Linsenstreuung kann durch die Punktspreizfunktion (PSF) angenähert charakterisiert werden. Diese Funktion gibt den beobachteten radial symmetrischen Lichtabfall einer Punktlichtquelle in völlig dunkler Umgebung an. Sie wird durch viele Parameter beeinflusst und kann je nach Bild unterschiedlich ausfallen. Daher zieht man es vor, die PSF aus jedem neu aufgenommenen HDR-Bild zu ermitteln.[15]
Um die PSF ausgehend von einem HDR-Bild zu berechnen, nutzt man die Tatsache aus, dass im Bild einige dunkle Pixel neben sehr hellen Pixeln liegen. Durch Ermittlung der minimalen Pixelwerte, die sich in bestimmten Abständen zu allen hellen Pixeln befinden, kann die PSF angenähert werden. Dazu wird der minimale Pixelwert bei einem bestimmten Abstand durch den Wert des hellen Pixels geteilt. Hier muss berücksichtigt werden, dass helle Pixel nahe beieinander liegen können und somit die durch einen bestimmten Radius definierten Kreise einander überlappen.
Sobald die PSF ermittelt wurde, kann die Linsenstreuung ausgefiltert werden, indem für jedes Pixel die durch den Pixelwert gewichtete PSF von dessen Umgebung abgezogen wird.
HDRI-Erzeugung mit dem Scanner
Ein optimal belichtetes und entwickeltes Negativ kann bis zu 12 Blendenstufen Kontrastumfang enthalten, die beim Digitalisieren mit einem Filmscanner in einem einzelnen Scan hardwarebedingt nicht komplett erfasst werden können. Multi-Exposure ist ein Verfahren, um einen möglichst großen Dynamikumfang beim Scannen von Durchsichtvorlagen wie Dias, Negativen und Filmstreifen zu erhalten. Dabei wird das Original mehrfach, aber mit unterschiedlichen Belichtungen, eingescannt. Aus den einzelnen Scans wird dann der HDR-Scan berechnet.
Literatur
- Jürgen Held: HDR-Fotografie. Das umfassende Handbuch. 4. Auflage, Rheinwerk Verlag, Bonn 2015, ISBN 978-3-8362-3012-4
- Reinhard Wagner: Profibuch HDR Fotografie, S. 107–157. Dpunkt, Heidelberg 2008, ISBN 3-89864-430-8
- Erik Reinhard u. a.: High Dynamic Range Imaging, S. 117–159. Morgan Kaufman, San Francisco 2006, ISBN 0-12-585263-0
Weblinks
- Homepage von Paul Debevec (englisch)
- Fotocommunity.de: DRI (siehe „Zweites Verfahren“)
Einzelnachweise
- S. Mann, R. W. Picard: Being “Undigital” with Digital Cameras: Extending Dynamic Range by Combining Differently Exposed Pictures. In IS&T’s 48th annual conference, S. 422–428. Society for Imaging Science and Technology, Washington DC 1995
- Paul Debevec, Jitendra Malik: Recovering High Dynamic Range Radiance Maps from Photographs. In SIGGRAPH 97 Conference Proceedings, S. 369–378. ACM SIGGRAPH, New York 1997, ISBN 0-89791-896-7 (PDF, 1,4 MB)
- Tomoo Mitsunga, Shree K. Nayar: Radiometric Self Calibration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Vol. 1, S. 374–380. IEEE, Fort Collins 1999, ISBN 0-7695-0149-4 (PDF, 950 kB)
- Reinhard u. a.: High Dynamic Range Imaging, S. 119 f.
- Sing Bing Kang u. a.: High Dynamic Range Video. In ACM SIGGRAPH 2003 Papers, S. 319–325. ACM, San Diego 2003, ISBN 1-58113-709-5
- Bruce Lucas, Takeo Kanade: An Iterative Image Registration Technique with an Application in Stereo Vision. In Seventh International Joint Conference on Artificial Intelligence (IJCAI-81), S. 674–679. Kaufmann, Los Altos 1981, ISBN 0-86576-059-4 (Online; PDF; 192 kB)
- Reinhard u. a.: High Dynamic Range Imaging, S. 122
- F. M. Candocia: Simultaneous Homographic and Comparametric Alignment of Multiple Exposure-Adjusted Pictures of the Same Scene. IEEE Transactions on Image Processing 12, 12 (Dec. 2003): 1485–1494, ISSN 1057-7149 (PDF, 880 kB (Memento des Originals vom 6. August 2007 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.)
- S. J. Kim, M. Pollefeys: Radiometric Self-Alignment of Image Sequences. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2004, S. 645–651. IEEE Computer Society, Los Alamitos 2004, ISBN 0-7695-2158-4 (PDF, 1,7 MB)
- Greg Ward: Fast, Robust Image Registration for Compositing High Dynamic Range Photographs from Hand-held Exposures. Journal of Graphics Tools 8, 2 (2003): 17–30, ISSN 1086-7651 (PDF, 4,8 MB)
- Reinhard u. a.: High Dynamic Range Imaging, S. 136
- Reinhard u. a.: High Dynamic Range Imaging, S. 145
- Reinhard u. a.: High Dynamic Range Imaging, S. 143
- Reinhard u. a.: High Dynamic Range Imaging, S. 147–151
- Reinhard u. a.: High Dynamic Range Imaging, S. 155–159