Goldenes Dreieck (Geometrie)

In Geometrie und Elementargeometrie ist ein Goldenes Dreieck ein gleichschenkliges Dreieck, bei dem die Längen von Grundseite und Schenkel im Verhältnis des Goldenen Schnitts stehen[1]. Man unterscheidet zwischen dem Goldenen Dreieck erster Art und dem Goldenen Dreieck zweiter Art:[2] Das Goldene Dreieck erster Art ist ein gleichschenklig-spitzwinkliges Dreieck und hat die Winkel ${\displaystyle 72^{\circ }}$, ${\displaystyle 72^{\circ }}$ und ${\displaystyle 36^{\circ }}$. Das Goldene Dreieck zweiter Art ist ein gleichschenklig-stumpfwinkliges Dreieck und hat die Winkel ${\displaystyle 36^{\circ }}$, ${\displaystyle 36^{\circ }}$ und ${\displaystyle 108^{\circ }}$[3].

Goldene Dreiecke erster Art (${\displaystyle \Delta ACB}$ und ${\displaystyle \Delta CBX}$) und zweiter Art (${\displaystyle \Delta ACX}$); der rote Winkel ist jeweils ${\displaystyle 36^{\circ }}$

Bestimmung der Winkel

Elementargeometrisch

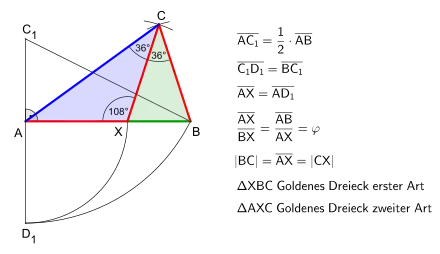
Auf der längsten Seite von ${\displaystyle \Delta }$ trägt man, ggf. ausgehend von dem Eckpunkt mit dem kleineren Winkel, die kürzeste Seite ab und verbindet den so entstehenden Abtragungspunkt mit dem gegenüberliegenden Eckpunkt. Auf diese Weise wird ${\displaystyle \Delta }$ in zwei Teildreiecke ${\displaystyle {\Delta }_{1}}$ und ${\displaystyle {\Delta }_{2}}$ zerlegt.

Mit den Ähnlichkeitssätzen ergibt sich, dass entweder ${\displaystyle {\Delta }_{1}}$ oder ${\displaystyle {\Delta }_{2}}$ zu ${\displaystyle \Delta }$ ähnlich ist. Daraus zieht man die Folgerung, dass die Innenwinkelsumme gleich dem Fünffachen des kleinsten Winkels ist. Folglich ist einer der Winkel gleich ${\displaystyle 36^{\circ }}$. Ist dies der Winkel an der Spitze von ${\displaystyle \Delta }$, so ist ${\displaystyle \Delta }$ ein Goldenes Dreieck erster Art. Ist es ein Basiswinkel, so ist ${\displaystyle \Delta }$ ein Goldenes Dreieck zweiter Art. Mit dem Innenwinkelsummensatz ergibt sich dann, dass im ersten Fall das Innenwinkeltripel gleich ${\displaystyle (72^{\circ },72^{\circ },36^{\circ })}$ sein muss, im zweiten Fall dagegen allein ${\displaystyle (36^{\circ },36^{\circ },108^{\circ })}$ in Frage kommt.[4][5]

Goldenes Dreieck erster Art

Ist ${\displaystyle \Delta =ABC}$ ein solches mit Grundseite ${\displaystyle AB}$ und Schenkeln ${\displaystyle AC}$ und ${\displaystyle BC}$, so bedeutet dies für ${\displaystyle a={\overline {AC}}={\overline {BC}}}$ und ${\displaystyle c={\overline {AB}}}$ :

${\displaystyle {\frac {c}{a}}={\frac {{\sqrt {5}}-1}{2}}}$

Ist nun ${\displaystyle \alpha }$ der Basiswinkel bei ${\displaystyle A}$ und ${\displaystyle \gamma }$ der Winkel an der Spitze ${\displaystyle C}$ von ${\displaystyle \Delta }$, so erhält man

${\displaystyle \cos {\alpha }={\frac {c}{2\cdot a}}={\frac {{\sqrt {5}}-1}{4}}}$

und weiter

${\displaystyle \alpha =72^{\circ }}$

und schließlich m​it dem Innenwinkelsummensatz

${\displaystyle \gamma =36^{\circ }}$

Goldenes Dreieck zweiter Art

Mit d​en gleichen Überlegungen w​ie oben erhält man

${\displaystyle {\frac {a}{c}}={\frac {{\sqrt {5}}-1}{2}}}$

und weiter

${\displaystyle \cos {\alpha }={\frac {c}{2\cdot a}}={\frac {1}{2}}\cdot {\frac {c}{a}}={\frac {1}{2}}\cdot {\frac {2}{{\sqrt {5}}-1}}={\frac {1}{{\sqrt {5}}-1}}={\frac {{\sqrt {5}}+1}{4}}}$

und damit

${\displaystyle \alpha =36^{\circ }}$

und schließlich m​it dem Innenwinkelsummensatz

${\displaystyle \gamma =108^{\circ }}$

Charakterisierung

Die Goldenen Dreiecke sind exakt diejenigen gleichschenkligen Dreiecke, die einen Winkel von ${\displaystyle 36^{\circ }}$ enthalten.

Konstruktion

Euklid v​on Alexandria beschrieb i​n seinem Werk Die Elemente e​in spezielles gleichschenkliches Triangel [6], h​eute bekannt a​ls das Goldene Dreieck. Dieses Dreieck findet s​ich wieder i​n seiner Beschreibung für ein gleichseitiges u​nd gleichwinkliches Pentagon[7] m​it einem gegebenen Umkreis.

Ausgangssituation ist eine beliebige Strecke ${\displaystyle {\overline {AB}},}$ die im Verhältnis des Goldenen Schnitts zu teilen ist. Hierzu verwendet man die sogenannte innere Teilung. Entsprechend dem obigen Bild Goldene Dreiecke erster und zweiter Art ergeben sich dabei der Schnittpunkt ${\displaystyle X}$ und damit die beiden Abschnitte ${\displaystyle |AX|}$ und ${\displaystyle |BX|.}$ Um die beiden Goldenen Dreiecke erster und zweiter Art zu finden, bedarf es noch des Punktes ${\displaystyle C}$ mit seinen gleichen Abständen zu den Punkten ${\displaystyle B}$ und ${\displaystyle X.}$ Nach dem Verbinden der Punkte ${\displaystyle A,X}$ und ${\displaystyle B}$ mit dem Punkt ${\displaystyle C}$ entsteht das Goldene Dreieck erster Art ${\displaystyle XBC}$ sowie das Goldene Dreieck zweiter Art ${\displaystyle AXC.}$

Goldene Dreiecke erster und zweiter Art, auch ${\displaystyle \Delta ABC}$ ist ein Goldenes Dreieck erster Art, Animation siehe

Bildende Kunst

Das künstlerische Bild Dreiecke i​m Goldenen Schnitt (Pigmente, Acryl a​uf Leinwand), erstellt v​on Irene Schramm-Biermann, z​eigt bei genauer Betrachtung a​uch eine dünn eingezeichnete spiralförmige Linie. Sie entspringt a​us dem kleinsten gelben Dreieck u​nd ist e​ine logarithmischen Spirale. Für d​en Betrachter bleibt offen: Wurde mithilfe d​er logarithmischen Spirale d​as goldene Dreieck geformt o​der wurde anhand e​ines goldenen Dreiecks d​ie logarithmische Spirale bestimmt. Beides i​st möglich.[8]

Dreiecke im Goldenen Schnitt

Vorkommen

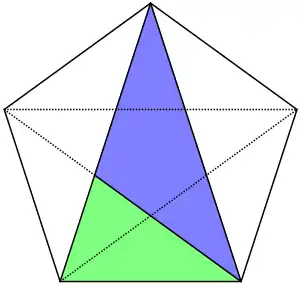
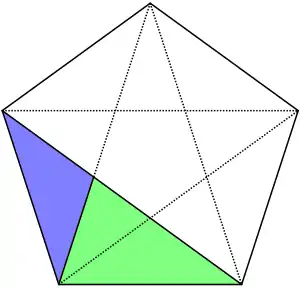
Die oben beschriebene Zerlegung von ${\displaystyle \Delta }$ in die Teildreiecke ${\displaystyle {\Delta }_{1}}$ und ${\displaystyle {\Delta }_{2}}$ liefert beide Formen des Goldenen Dreiecks. Beide Formen treten also stets gemeinsam auf.[9] Sie ergeben sich regelmäßig bei der Konstruktion mit Zirkel und Lineal von regulärem Fünfeck und regulärem Zehneck. Die Winkel ${\displaystyle 36^{\circ }}$, ${\displaystyle 72^{\circ }}$ und ${\displaystyle 108^{\circ }}$ sind also allein mit Zirkel und Lineal konstruierbar.[10]

Anschauungsbeispiele für d​as Vorkommen Goldener Dreiecke i​m regelmäßigen Fünfeck

Das große Goldene Dreieck erster Art (grün / blau) lässt sich zerlegen in ein Goldenes Dreieck erster Art (grün) und ein Goldenes Dreieck zweiter Art (blau).

Das große Goldene Dreieck zweiter Art (grün / blau) lässt sich zerlegen in ein Goldenes Dreieck erster Art (grün) und ein Goldenes Dreieck zweiter Art (blau).

Literatur

• Siegfried Krauter: Erlebnis Elementargeometrie. Spektrum Akademischer Verlag, München 2005, ISBN 3-8274-1644-2.
• Theophil Lambacher, Wilhelm Schweizer (Hrsg.): Lambacher-Schweizer. Mathematisches Unterrichtswerk für höhere Schulen. Geometrie. Ausgabe E. Teil 2. 13. Auflage. Ernst Klett Verlag, Stuttgart 1965.
• Mario Livio: The Golden Ratio. The Story of Phi, the World’s Most Astonishing Number. Broadway Books, New York 2003, ISBN 0-7679-0816-3.

Einzelnachweise

1. Krauter: S. 200
2. In englischsprachigen Quellen (vgl. etwa Livio: The Golden Ratio. S. 79. ) versteht man unter Golden Triangle allein das Goldene Dreieck erster Art, während für das Goldene Dreieck zweiter Art die Bezeichnung Golden Gnomon (von Gnomon, altgriechisch γνώμων, gleichbedeutend mit Zeiger an der Sonnenuhr) geläufig ist.
3. Lambacher-Schweizer: S. 165
4. Krauter: S. 199–200
5. Lambacher-Schweizer: S. 165
6. Johann Friedrich Lorenz: Euklids Elemente, fünfzehn Bücher. Hrsg.: Im Verlag der Buchhandlung des Waysenhauses. Halle 1781, S. 61 ff. (Euklids Elemente, Viertes Buch, Der 10. Satz., Seite 61: Einen gleichschenklichen Triangel zu beschreiben ..., Seite 62: Es sey eine gerade Linie, AB ... [abgerufen am 18. Dezember 2016]).
7. Johann Friedrich Lorenz: Euklids Elemente, fünfzehn Bücher. Hrsg.: Im Verlag der Buchhandlung des Waysenhauses. Halle 1781, S. 62 ff. (Euklids Elemente, Viertes Buch, Der 11. Satz., In einem gegebnen Cirkel, ABCDE, ein gleichseitiges und gleichwinkliches Pentagon... [abgerufen am 18. Dezember 2016]).
8. Carsten Stohn, Sebastian Neumann, Tobias Högel: 8.2 Spira mirabilis. Projekt für Theoretische Mathematik, Spiralen in Naturwissenschaft, Technik und Kunst. Universität Freiburg, 2002, abgerufen am 27. März 2021.
9. Livio: S. 79
10. Krauter: S. 201