Gabriel Lamé
Gabriel Lamé (* 22. Juli 1795 in Tours; † 1. Mai 1870 in Paris) war ein französischer Mathematiker und Physiker.

Nach Arbeiten mit Émile Clapeyron in Sankt Petersburg war Lamé ab 1832 Professor an der École polytechnique in Paris.
Leistungen
Er wurde berühmt durch seine Arbeiten zur Differentialgeometrie und Beiträge zur mathematischen Physik, insbesondere zur Lösung der Wärmeleitungsgleichung, bei der er erstmals mit einem gekrümmten Koordinatensystem arbeitete.
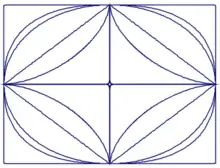
Nach Lamé wurden von diesem untersuchte und beschriebene ellipsenartige Kurven benannt (Lamésche Kurven):
mit n: beliebige positive reelle Zahl. Es handelt sich um eine Verallgemeinerung der mathematischen Beschreibung der Kegelschnitte Kreis und Ellipse. Der dänische Wissenschaftler Piet Hein (1905–1996) führte für die Laméschen Kurven den Begriff Superellipse ein.
Der Satz von Lamé (1844) gibt mit der Fibonacci-Folge (Laméschen Zahlenreihe) die Obergrenze für den Aufwand beim Euklidischen Algorithmus an.
Die sogenannte Lamésche Zahlenreihe (Teil der Fibonacci-Folge) findet in der Typographie Verwendung. Die in ihr beschriebene Folge von 3, 5, 8, 13, 21 usw. wird dort in Form von Teilungsverhältnissen wie 5:8 oder 8:13 usw. (Goldener Schnitt) bei Satzspiegelkonstruktionen angewandt, da diese Verhältnisse als besonders harmonisch empfunden werden.
Die Lamé-Konstanten beschreiben zwei Materialkonstanten, die insbesondere in der Elastizitätstheorie und in der Strömungslehre angewendet werden.
1847 stellte er einen Beweisversuch der Fermat-Vermutung vor, der sich zwar als fehlerhaft erwies, aber nach der Kritik durch Joseph Liouville, der auf die Notwendigkeit des Beweises der Eindeutigkeit der Primfaktorzerlegung für die Arithmetik in den beim Beweis betrachteten Kreisteilungskörpern hinwies, zu fruchtbarer neuer Forschung in der algebraischen Zahlentheorie führte (Ernst Eduard Kummer u. a.). Am Ende bewies Lamé aber den Fall n=7.
Im Jahre 1861 veröffentlichte er sein Buch Leçons sur la théorie analytique de la chaleur, in dem er die These vertrat, an kristallisierenden Lösungen bildeten sich „concamérations polyedriques“ („vielflächige Wölbungen“). Diese Annahme erschien damals noch fremdartig, bestätigte sich aber später durch die Entdeckung der Flüssigkristalle.
Mitgliedschaften
Am 16. Dezember 1829 (Julianischer Kalender) wurde Lamé als korrespondierendes Mitglied in die Russische Akademie der Wissenschaften in St. Petersburg aufgenommen.[1] 1838 wurde er zum korrespondierenden Mitglied der Preußischen Akademie der Wissenschaften gewählt.[2] 1843 wurde er Mitglied der Académie des sciences in Paris.[3]
Ehrungen
Lamé wurde als einer von 72 Wissenschaftlern und Ingenieuren namentlich auf dem Eiffelturm verewigt. Der Mondkrater Lamé ist nach ihm benannt.
Schriften (Auswahl)
- Leçons sur la théorie analytique de la chaleur. Mallet-Bachelier, Paris 1861 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 12. Oktober 2021]).
Literatur
- J. Allard: Notes on squares and cubes. In: Mathematical Magazine, 37/1964, S. 210–214
- N. T. Gridgeman: Lamé Ovals. In: The Mathematical Gazette, 54/1970, S. 31–37
- Karl-Eugen Kurrer: The History of the Theory of Structures. Searching for Equilibrium. Ernst & Sohn, 2018, ISBN 978-3-433-03229-9, S. 437 ff. und S. 1021 (Biografie).
Weblinks
- John J. O’Connor, Edmund F. Robertson: Gabriel Lamé. In: MacTutor History of Mathematics archive.
- Eric W. Weisstein: Superellipse. (MathWorld – A Wolfram Web Resource)
- Lamésches Oval / Superellipse (Java-Applet). activeart.de
Einzelnachweise
- Korrespondierende Mitglieder der Russischen Akademie der Wissenschaften seit 1724: Lamé, Gabriel. Russische Akademie der Wissenschaften, abgerufen am 8. Januar 2020 (russisch).
- Historische Akademiemitglieder: Gabriel Lamé. Berlin-Brandenburgische Akademie der Wissenschaften, abgerufen am 8. Januar 2020.
- Verzeichnis der Mitglieder seit 1666: Buchstabe L. Académie des sciences, abgerufen am 8. Januar 2020 (französisch).