Fundamental Modeling Concepts
Fundamental Modeling Concepts (FMC) sind eine semi-formale Methodik zur Kommunikation über komplexe Softwaresysteme.
Geschichte
Seit Ende der 1970er Jahre wurden ihre Grundlagen von Siegfried Wendt und seinen Mitarbeitern und Schülern an der Universität Kaiserslautern entwickelt. An dem 1999 unter Leitung von Siegfried Wendt gegründeten Hasso-Plattner-Institut an der Universität Potsdam wurden diese Konzepte zunächst unter dem Namen SPIKES (Structured Plans for Improving Knowledge Transfer in Engineering of Systems) gelehrt, bevor sie im Jahr 2001 den Namen FMC (Fundamental Modeling Concepts) erhielten.
Relevanz
Mit FMC werden eine Vielzahl von Softwaresystemen analysiert, entworfen und dokumentiert. Bekannter Nutzer ist u. a. das Walldorfer Softwarehaus SAP, welches die SAP R/3 Architektur damit dokumentiert. Hasso Plattners Begeisterung für diese Methodik resultierte in der Gründung des HPI (Hasso-Plattner-Institutes), welches die Lehren von FMC in der Vergangenheit in der universitären Grundausbildung vermittelte.
Einführung
Nach FMC gibt es drei miteinander verwobene Arten, Softwaresysteme zu betrachten:
- Aufbau des Systems
- Abläufe im System
- Wertebereiche
Für jede dieser Betrachtungsweisen gibt es einen Diagrammtyp, mit dessen Hilfe der jeweilige Aspekt zeichnerisch dargestellt werden kann. Die resultierenden, meist leicht zu erstellenden, aber auch leicht zu verstehenden Diagramme haben FMC unter seinen Anhängern populär gemacht.
Grundsätzlich dienen FMC-Diagramme einem von zwei Zwecken: Sie sollen entweder von einer Gruppe verwendet werden, um über ein Softwaresystem zu kommunizieren, oder sie werden benutzt, um andere (Entwickler, Kunden, Manager etc.) in ein Softwaresystem einzuführen. Im ersten Falle werden die Diagramme meist etwas umfangreicher, um die Kommunikation über komplexere Zusammenhänge zu erleichtern; im zweiten Fall werden aus didaktischen Gründen zumeist kleine Diagramme mit wenigen Komponenten verwendet. Immer aber sollen Ästhetik und Anschaulichkeit im Vordergrund stehen, da wesentlicher Antrieb in der Verwendung von FMC die Förderung der Kommunikation sein soll. Deshalb sind die Diagramme zwar wichtigster Bestandteil von FMC, erübrigen aber keinen Kommentar.
Diagramme
Allen Diagrammen ist gemein, dass es sich um sogenannte bipartite Graphen handelt. Ein bipartiter Graph ist dabei ein Graph, dessen Knoten aus zwei verschiedenen Klassen stammen, mit der Bedingung, dass kein Knoten direkt mit Knoten aus seiner Klasse verbunden sein darf. Die Knoten der einen Klasse werden immer als Rechteck gezeichnet (eckiger Knoten), die Knoten der anderen als Kreis, Ellipse, Oval oder Stadion (Rechteck mit zwei angesetzten Halbkreisen an zwei gegenüberliegenden Seiten) gezeichnet (runder Knoten).
Außerdem können in allen Diagrammen dargestellte Zusammenhänge nahezu beliebig in anderen Diagrammen gleichen Typs verfeinert oder abstrahiert werden. Damit können alle für die Software relevanten Abstraktionsstufen eines Systems mit der gleichen Methodik dargestellt werden.
Aufbaudiagramme
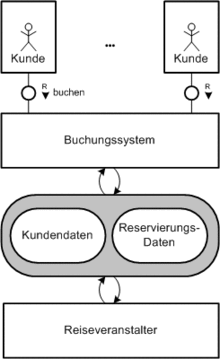
Ein Aufbaudiagramm beschreibt, wie eine Menge von Systemkomponenten zueinander in Beziehung stehen. Zu diesem Zwecke wird jede Komponente als Akteur, Kanal oder Speicher identifiziert. Kanäle und Speicher werden auch als passive Komponenten bezeichnet, Akteure entsprechend als aktive Komponenten. Dabei können passive Komponenten nicht direkt mit anderen passiven Komponenten in Beziehung stehen, ebenso wenig wie aktive mit aktiven. Daraus resultiert ein bipartites Systemverständnis, das seinen Niederschlag in bipartiten Aufbaubildern findet.
Struktur
In Aufbaubildern werden aktive Komponenten durch eckige Knoten und passive Komponenten durch runde Knoten dargestellt, wobei Kanäle meist durch einen kleineren Kreis, und Speicher durch ein größeres Oval oder Stadion dargestellt werden. Die Kanten (Verbindungslinien) zwischen Speichern und Akteuren müssen gerichtet sein, zwischen Kanälen und Akteuren können sie auch ungerichtet sein. Die Richtung hat folgende Bedeutung:
- Speicher/Kanal → Akteur: Akteur liest aus Speicher bzw. empfängt vom Kanal
- Akteur → Speicher/Kanal: Akteur schreibt in Speicher bzw. sendet über Kanal
Es gibt keine Kanten, die in beide Richtungen gerichtet sind. Stattdessen werden, um auszudrücken, dass ein Akteur sowohl aus einem Speicher liest als auch in diesen schreibt, zwei entgegengesetzt gerichtete Kanten verwendet (auch als modifizierender Zugriff bezeichnet). Bei Kanälen wird im Gegensatz dazu eine ungerichtete Kante benutzt.
Knoten können gruppiert werden, um Gemeinsamkeiten zu veranschaulichen. Dazu wird einfach ein weiterer Knoten eingeführt, der diese anderen Knoten enthält. So können einige Akteure und Speicher Teil eines größeren Akteurs sein, dessen innerer Aufbau dargestellt werden soll, oder es gibt eine Menge von Speichern, auf die vom selben Akteur zugegriffen werden soll.
Eine spezielle Form des Kanals ist ein Request/Response-Kanal, bei dem eine benutzende Komponente einen Dienst einer anderen Komponente aufruft und eine entsprechende Antwort erhält. Diese Kanäle werden mit einem "R" und einem Pfeil gekennzeichnet, der von der aufrufenden zur aufgerufenen Komponente zeigt.
Strukturvarianz
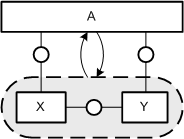
Die Struktur vieler Softwaresysteme kann sich zur Laufzeit ändern. Diese Strukturvarianz wird in FMC folgendermaßen interpretiert: Das betroffene Teilsystem wird unabhängig von seiner tatsächlichen Struktur als Speicher aufgefasst, das von einem nicht in diesem Teilsystem enthaltenen Akteur modifiziert werden kann. Entsprechend werden im Aufbaubild ein Speicher (zur Unterscheidung mit gestrichelter Außenlinie), der dieses Teilsystem enthält, und der modifizierende Zugriff des Strukturvarianz-Akteurs auf diesen Speicher eingezeichnet.
Ablaufbilder
Abläufe werden mit einer Klasse von Petri-Netzen, den Bedingungs-Ereignis-Netzen, dargestellt, da diese ebenfalls bipartit sind. In FMC-Petrinetzen kann jede Stelle normalerweise nur eine Marke aufnehmen, so dass die Schaltregel lautet:
Eine Transition schaltet genau dann, wenn alle Eingangsmarken belegt sind und alle Ausgangsmarken, die nicht gleichzeitig Eingangsmarken sind, frei sind.
Zusätzlich gibt es noch Stellen, die beliebig viele Stellen aufnehmen können und durch einen Doppelkreis dargestellt werden. Besondere ,unendliche‘ Stellen sind Stack-Stellen und Rücksprungstellen.
Außerdem gibt es in FMC-Petrinetzen das Mittel der Auflösung von Konflikten über Bedingungsevaluierung. Gehen von einer Stelle mehrere Kanten ab, so können Bedingungen an diese Kanten geschrieben werden, anhand derer bestimmt werden kann, in welchem Fall welche Transition schaltet.
Wertebereichsbilder
Hierbei handelt es sich um leicht veränderte und erweiterte Entity-Relationship-Diagramme. Entitäten (Gegenstände) sind in FMC-Diagrammen runde Knoten, Relationen eckige. Entitäten können mit Attributen behaftet werden, die als Liste im Knoten der Entität notiert werden. Abstraktion ermöglicht es Entitäten, Relationen zu enthalten, so dass Relationen in Relation zu anderen Entitäten oder Relationen stehen können. Partitionen von Entitäten werden entweder dargestellt, indem die Sub-Entitäten in die zu partionierende Entität gezeichnet werden, oder durch das dreieckige Partitionssymbol (das sozusagen die "Partitionsrelation" darstellt).
Schichtendiagramme
Zur exemplarischen Darstellung von quadratischen Relationen, d. h. Relationen auf einer Menge von Elementen, können sogenannte Schichtungsdiagramme genutzt werden. Dabei handelt es sich um die verkürzte Darstellung einer Matrixdarstellung, mit der sich beliebige zwei-stellige Relationen darstellen lassen. Beispielsweise kann dieser Diagrammtyp dazu genutzt werden, die Aufrufschichtung von Prozeduren oder die Abhängigkeiten der Pakete innerhalb eines Computerprogrammes darzustellen (wobei der Rekursionsfall ebenfalls darstellbar ist).
Obwohl diese Form der Darstellung in einer Reihe FMC-basierter Modellierungsdokumente verwendet wird, ist sie nicht als konzeptioneller Bestandteil von FMC angesehen. Vielmehr handelt es sich um die fallweise nützliche Ergänzung der Beschreibung, so wie für bestimmte andere Aspekte UML-Klassendiagramme oder Bildschirmfotos zweckmäßige Beschreibungsmittel sind.
Siehe auch
- Unified Modeling Language, eine graphische Modellierungssprache zur Spezifikation, Konstruktion und Dokumentation von Software-Teilen und anderen Systemen
Literatur
- Siegfried Wendt: Nichtphysikalische Grundlagen der Informationstechnik. Interpretierte Formalismen. 2. Auflage. Springer-Verlag, Berlin Heidelberg 1991, ISBN 3-540-54452-6 (PDF; 7,31MB).
- Eine PDF-Fassung, die durch den Autor nach Einstellung der ursprünglichen Verlagsauflage freigegeben wurde. Auch wenn dieses Werk nicht speziell auf die Beschreibung von FMC abzielt, sondern in Inhalt und Struktur sehr viel grundsätzlicher angelegt ist, so wird der interessierte Leser hier dennoch das FMC zugrundeliegende Erkenntnisfundament erkennen.
- Andreas Knöpfel, Bernhard Gröne, Peter Tabeling: Fundamental Modeling Concepts: Effective Communication of IT Systems, Wiley 2006, ISBN 0-470-02710-X
- Peter Tabeling: Softwaresysteme und ihre Modellierung, Springer-Verlag Berlin Heidelberg 2005, ISBN 3-540-25828-0