Francesco Torniello
Francesco Torniello da Novara (* um 1490; † 1589 in Treviglio, Italien) war ein Mailänder Typograf, Schriftsteller und Franziskaner, der durch die erste schriftliche geometrische Spezifikation einer Schriftart für lateinische Versalien bekannt wurde. Er kann daher als Pionier der mathematischen Typografie angesehen werden.

Leben
Die Tornielli waren in der Renaissance eine vermögende, weitverzweigte Familie, von der einige Mitglieder in Barengo lebten, das zur Provinz Novara gehört, und einige in der Stadt Novara selbst. Es gibt jedoch keine überlieferten Belege, dass Francesco einem dieser beiden Familienzweige angehörte und von dort dann später nach Mailand zog. Zwei Brüder, Francesco und Giovanni Antonio Torniello da Novara, sind 1525 in Mailand urkundlich belegt, als Herzog Francesco Sforza ihnen das Mailänder Bürgerrecht verlieh.
In dem Werk Museo Novarese des Mailänder Historikers Lazzaro Agostino Cotta (1645–1719) von 1701 wird Francesco Torniello als Experte in Geometrie und Arithmetik beschrieben, der als Schriftsteller tätig war. Als einziges Werk überliefert ist jedoch nur ein Buch mit dem Titel Opera del modo de fare le littere maiuscole antique, das 1517 in Mailand erschien.
Ein Francesco Torniello trat 1519 in den Orden der Franziskaner ein und erlangte durch seine Predigten einige Bekanntheit. Es lässt sich nicht mit Sicherheit belegen, dass es sich um ein und dieselbe Person handelt, aber es sprechen nach Einschätzung von Giovanni Mardersteig mehrere Indizien dafür: So passt das Alter zusammen und auch der Franziskaner wird in Bezug auf seine berufliche Tätigkeit vor seinem Eintritt in den Orden als Schriftgelehrter beschrieben. Der Franziskaner veröffentlichte dann noch ein weiteres Werk mit dem Titel De Unitate Ecclesia Dei, von dem jedoch kein Exemplar mehr bekannt ist. Er starb 1589 in dem Franziskanerkloster in Treviglio in sehr hohem Alter.
Werk
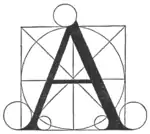
Dank der ausführlichen und verehrenden Referenz von Tornielli in seinem Werk an Luca Pacioli wissen wir, dass er ihm entweder begegnet sein muss oder ihm zumindest das Werk Divina Proportione zur Verfügung stand. Dieses Werk enthält u. a. geometrische Darstellungen aller lateinischen Großbuchstaben. Paciolis Schriftart stellte zu dieser Zeit den Höhepunkt einer Entwicklung in der Renaissance dar, die danach strebte, die lateinischen Buchstaben alter Inschriften und Grabsteine möglichst originalgetreu zu übernehmen und sie in ihrer geometrischen Ausgestaltung zu perfektionieren. Diese Entwicklung begann 1460 mit einer im Vatikan archivierten Handschrift von Felice Feliciano (1433–1479) und wurde von Damianus Moyllus (1439–1500) 1483 oder 1484 fortgesetzt. Diese Schriftarten waren damals noch nicht primär für den Buchdruck gedacht, sondern als Vorlage für künstlerische Inschriften. Als Werkzeuge für den Entwurf der einzelnen Buchstaben standen nur Lineal und Zirkel zur Verfügung. Bis einschließlich des Werks Paciolis wurden allerdings nur die fertigen Entwürfe zusammen mit einigen Konstruktionselementen wie den verwendeten Kreisen und dem umgebenden Rechteck oder Quadrat dargestellt. Eine vollständige schriftliche Spezifikation passend zu den Diagrammen fehlte jedoch.
In dieser Hinsicht betrat Torniellos Werk Opera del modo de fare le littere maiuscole antique, das 1517 in Mailand von Gotardo da Ponte gedruckt und veröffentlicht wurde, Neuland. Das beginnt damit, dass Torniello ein 18×18-Raster definierte, das als Koordinatensystem dient. Die doppelte Seitenlänge eines Rasterfeldes wurde dabei als Punkt definiert. Dies ist die erste bekannte Definition eines Punktes als typografische Maßeinheit. Es ist allerdings nicht anzunehmen, dass Pierre Simon Fournier das Werk von Torniello kannte, als er 1737 ebenfalls den Punkt als typografische Maßeinheit einführte. Der Punkt als Maßeinheit und das Raster erleichterten Torniello sehr die geometrische Spezifikation in Schriftform, wie folgendes Beispiel für den Buchstaben „A“ illustriert:
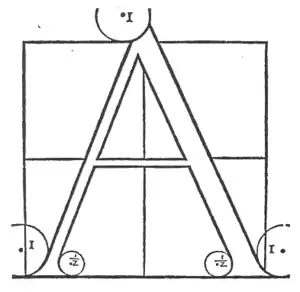
Der Buchstabe A wird vom Quadrat geformt. Die Dicke des rechten Beins sollte ein Neuntel der Vertikalen betragen; es sollte außerhalb des Quadrats beginnen, wo es den Kreis berührt, der durch die oben liegende Horizontale einen halben Punkt links vom Mittelpunkt durchgeht, und in der unten liegenden Ecke des Quadrats endet mit den Kreisen, wie Du sie eingezeichnet siehst. Alle äußeren Kreise haben einen Radius von einem Punkt und die inneren einen Radius von einem halben Punkt, gemessen von dem Mittelpunkt eines Kreises bis zu seinem Umfang. Das linke Bein sollte die halbe Dicke des rechten haben und die Innenlinie sollte einen Startpunkt haben, der mit der Mitte der oberen Linie des Quadrats zusammentrifft, und einen halben Punkt vor der Grundlinie enden, einen Punkt innerhalb der linken Vertikalen des Quadrats. Die Querlinie sollte ein Drittel der Dicke des rechten Beines aufweisen, wobei die obere Linie mit der Horizontalen in der Mitte des Quadrats zusammentreffen sollte.
 |
 |
 |
 |
 |
 |
 |
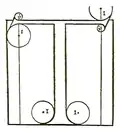 |
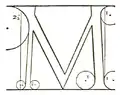
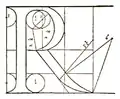
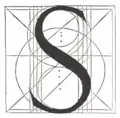
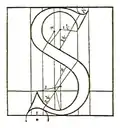
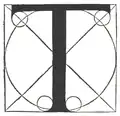
| Vergleich einiger Versalien von Pacioli (links) und Torniello (rechts) | |
Während Torniello weitgehend die Entwürfe von Pacioli übernahm, wich er bei den Buchstaben „M“, „R“, „S“ und „T“ deutlich von seinem Vorbild ab. Insbesondere die Buchstaben „S“ und „T“ wurden um kalligraphische Details bereichert, die auch von späteren Typografen kopiert wurden. So findet sich beispielsweise die Gestaltung der parallelen schräg geschnittenen oberen Serifen des „T“ in dem Alphabet von Albrecht Dürer wieder. Nur das „M“ wurde in der vergleichenden Analyse von Giovanni Mardersteig als weniger gelungen betrachtet. Ferner ergänzte Torniello sein Alphabet um das „Z“, was als Beleg betrachtet werden kann, dass diese Schriftarten auch zunehmend für nicht-lateinische Texte verwendet wurden.
An den Buchstaben „R“ und „S“ lassen sich auch weitere Eigenheiten der Konstruktionszeichnungen von Torniello erkennen. So zeichnete er für alle verwendeten Kreisbögen jeweils das vollständige Kreissegment ein zusammen mit der Angabe des jeweiligen Radius, der in Punkten gemessen wurde. Im begleitenden Text wurden die zugehörigen Koordinaten spezifiziert.
Weitere Entwicklung in der Renaissance
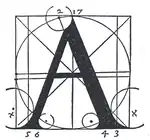
Torniellos Werk und die Alphabete seiner Vorgänger, insbesondere von Pacioli und Sigismondo Fanti (1514), beeinflussten wesentlich die weitere Entwicklung. Giovam Baptista Verini publizierte 1526 in Florenz im dritten Band zu seinem Werk Luminario ein Alphabet, das sich weitgehend von den Entwürfen von Pacioli und Fanti ableitete, aber von Torniello die Definition des Punkts als neunten Teil der Seitenlänge übernahm. Im Unterschied zu Pacioli und Torniello fallen die sehr viel größeren Kreise bei den Serifen auf, so dass diese deutlich schwerer wirken.
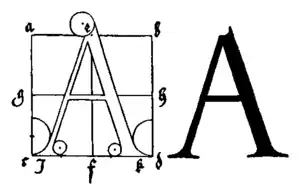
Im Jahr 1528 veröffentlichte Albrecht Dürer in Nürnberg seine bereits 1525 entstandenen Entwürfe zu seinem Alphabet. Dürer kannte seine italienischen Vorgänger recht gut und ließ sich hauptsächlich von Pacioli und Torniello leiten. Als erster stellte er beide Varianten, die ausgefüllten Buchstaben in Anlehnung an Pacioli und die Konstruktionsskizzen entsprechend dem Vorbild von Torniello, nebeneinander dar. Die Rasterung übernahm Dürer ebenfalls von Torniello. Die Größen der Serifen ähneln jedoch eher denen von Pacioli. Sie sind damit etwas weniger zierlich als die von Torniello, jedoch deutlich kleiner als die von Verini.
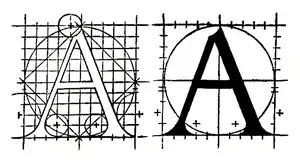
Kurz danach, aber in voller Kenntnis des Werks von Albrecht Dürer und der italienischen Vorbilder veröffentlichte Geoffroy Tory 1529 sein Werk Champ Fleury in Paris. Er übernahm dabei von Albrecht Dürer die duale Darstellung entsprechend der Torniellos und Paciolis und verwandte ebenfalls ein Raster, das aber im Unterschied zu dem von Torniello auf 10×10 dimensioniert ist. Für die Serifen kamen jedoch viel größere Kreise zum Einsatz, die eher denen von Verini gleichen als den kleineren Kreisen von Torniello oder Pacioli.

Der Abschied vom Zirkel als Werkzeug der Typografie wurde von Ludovico degli Arrighi 1523 und insbesondere von Francesco Cresci in seinem Werk Essemplare di più sorti lettere von 1560 eingeleitet. Cresci studierte erneut die antiken Inschriften und kam zu dem Schluss, dass auf dem Zirkel beruhende Konstruktionen den Originalen nicht gerecht werden. Beispielsweise basiert das nebenstehende „B“ auf der entsprechenden Form in der Inschrift am Piedestal der Trajanssäule in Rom. In seiner Zusammenfassung schreibt Cresci daher abschließend: Ich bin zu dem Schluss gekommen, dass Euklid, der Prinz der Geometrie, wenn er zu unserer Welt zurückkehren würde, niemals darauf kommen würde, dass die Kurven der Buchstaben mit Hilfe von mit Zirkeln gezogenen Kreisen so konstruiert werden könnten, dass sie den Proportionen und dem Stil der antiken Buchstaben entsprechen.
Literatur
- Luca Pacioli: De Divina Proportione. Antonio Capella, Venedig 1509. (Von diesem Werk existiert ein Nachdruck, der 1998 mit einem Vorwort von Fabio Massimo Bertolo von den Tipografi Associati Sassari herausgegeben wurde, außerdem eine elektronische Online-Version der zweisprachigen Ausgabe von Constantin Winterberg, 1888: . Das Werk enthält im Anhang das Alphabet von Pacioli.)
- Francesco Torniello da Novara: Opera del modo de fare le littere maiuscole antique. Gotardo da Ponte, Milano 1517. (Von dem originalen Werk sind nur noch vier Exemplare bekannt, eines davon in der Biblioteca Columbina von Sevilla, eines in der Pepys Library von Cambridge und zwei in der Biblioteca Ambrosiana von Mailand.)
- Francesco Torniello, Luca Pacioli und Giovanni Mardersteig: The Alphabet of Francesco Torniello da Novara. Officina Bodoni, Verona 1971. (Dieses Werk enthält eine vollständige Reproduktion des Werks von Francesco Torniello. Hinzu kommt eine Gegenüberstellung mit dem Alphabet von Luca Pacioli und einer ausführlichen Einführung von Giovanni Mardersteig, die eine wichtige Grundlage für diesen Artikel bildete. Von diesem Buch wurden insgesamt nur 160 Exemplare gedruckt.)
- Donald M. Anderson: Cresci and His Capital Alphabets. Visible language 4/1971, Seiten 331–352. (Der Artikel geht ausführlich auf die gesamte typografische Geschichte der Renaissance ein, um die teilweise sehr scharfe Auseinandersetzung von Cresci mit seinen Vorgängern genauer zu beleuchten.)
- Donald E. Knuth: Mathematical Typography. Bulletin of the American Mathematical Society (new series) 1/March/1979, Seiten 337–372. Wurde erneut veröffentlicht in dem Sammelband Donald E. Knuth: Digital Typography, CSLI Publications, Stanford 1999. ISBN 1-57586-010-4. (Dieser Artikel geht u. a. in einem Überblick auch auf die Geschichte mathematischer Definitionen für Buchstaben ein.)
- Donald E. Knuth: The Letter S. The Mathematical Intelligencer 2/1980, Seiten 114–122. Wurde erneut veröffentlicht in dem Sammelband Donald E. Knuth: Digital Typography, CSLI Publications, Stanford 1999. ISBN 1-57586-010-4. (Dieser Artikel geht detailliert auf die Problematik ein, den Buchstaben „S“ darzustellen. Hierbei wird u. a. auch die geometrische Beschreibung für „S“ von Francesco Torniello vorgestellt und anschließend in die Sprache METAFONT übertragen und danach etwas vom Autor ergänzt und verfeinert.)